Шаг 1. заносим данные в таблицу SPSS
| Определение переменных. Чтобы задать переменную, нужно в Редакторе данных SPSSдважды щелкнуть на ячейке с надписью var или щелкните на ярлычке Вид переменной (Variable view) на нижнем краю таблицы. В обоих случаях вы перейдете в режим просмотра переменных, который обеспечивает редактор данных. Переменная обладает следующими реквизитами: 1. Имя (Name). Введите в текстовом поле Имя (Name) выбранное имя переменной. При выборе переменной следует соблюдать определенные правила: - Имя переменной должно начинаться с буквы. - Имя переменных могут содержать буквы и цифры. Кроме того, допускаются специальные символы _ (подчеркивание),. (точка), а также символы @ и #. - Последний символ имени не может быть точкой или знаком подчеркивания (_). - Длина имени переменной не должна превышать восьми символов (для 11 и более ранних версий). - Имена переменных нечувствительны к регистру, то есть прописные и строчные буквы не различаются. 2. Тип переменной (Type).Для каждой переменной определяется свой тип, при этом по умолчанию указывается цифровой. 3. Разрядность (Width).Длина переменной. 4. Десятичные разряды (Decimal) – количество знаков после запятой. 5. Метка переменной (Label). Метка переменной – это описательная этикетка, которую вы можете назначить для каждой переменной, то есть позволяющая описать переменную более подробно. 6. Значение (Values). Метка значений – это название, позволяющее более подробно описать возможные значения переменной. 7. Утерянные данные (Missing). 8. Столбцов (Columns).Поле Столбцы (Columns) определяет ширину, которую будет иметь в таблице данный столбец при отображении значений. Ширину столбца также можно изменить непосредственно в о окне редактора данных. По умолчанию ширина столбцов равна 8. 9. Выравнивание (Alignment). Здесь можно задать вид выравнивания значений, т.е. определить, как они будут отображаться в таблице. Возможные виды выравнивания – «Right» (по правому краю), «Left» (по левому краю) и «Center» (по центру). 10. Шкала измерения (Measure). Здесь можно задать шкалу переменной, которая может быть номинальной (шкала наименования), порядковой или метрической. По умолчанию принимается метрическая шкала измерения. Правда, это различие имеет значение только при создании интерактивных графиков, где номинальная и порядковая шкала измерений объединяются в категориальный тип. |
Определение переменных:
1. Имя - вводите собственное обозначение переменных.
2. Тип переменной – цифровой.
3. Разрядность – 6.
4. Десятичные разряды – максимум 3.
5. Метка переменной – опишите переменные.
Оставить пустой.
7. Утерянные данные – не заполнять.
8. Столбцы – по умолчанию 8.
9. Выравнивание – справа.
10. Шкала измерений – интервальная (масштабирование).
Рис.1 Редактор данных: просмотр данных
Шаг 2. Выберите в меню команды Анализ – Регрессия – Линейный…
Рис 2. Выберите в меню команды Анализ (Analyze) – Регрессия (Regression)
Появится диалоговое окно Линейная регрессия (Linear Regression) (см. рис. 3):
Рис. 3 Диалоговое окно: Линейная регрессия
| Диалоговое окно линейная регрессия содержит следующие компоненты: - Список исходных переменных – список всех переменных в файле данных. В данный момент в списке исходных переменных присутствуют следующие переменные: x (количество концов проводов в месте проверки),y ( время на одно место проверки, мин. ) Перед именем каждой переменной стоит значок, по которому можно определить, является ли эта переменная численной или строковой. -Зависимая переменная (Dependent). -Независимая переменная (Independent). -Переменная отбора (Selection variable) – позволяет выбрать переменную отбора для того, чтобы ограничить анализ подмножеством наблюдений, имеющих конкретные значения для этой переменной. -Метки наблюдений – указать переменную для идентификации наблюдений (точек) на графиках. -Метод (Method) – позволяет объединять независимые переменные в блоки и задавать разные методы ввода в уравнение регрессии для разных подмножеств переменных. -Командные кнопки: 1. OK – кнопка ОК запускает соответствующую процедуру. Одновременно она закрывает диалоговое окно. 2. Вставка (Paste) – эта кнопка переносит выбранный в диалоговом окне синтаксис команды в редактор синтаксиса (Файл (File) – Открыть (Open) - Синтаксис (Syntax)). Здесь можно отредактировать синтаксис команды и дополнить его другими опциями, недоступными в диалоговом окне. 3. Сброс (Reset) – эта кнопка отменяет перенос в целевой список переменных. 4. Отмена (Cancel) – эта кнопка отменяет все изменения, сделанные с момента последнего открытия диалогового окна, и закрывает его. 5. Помощь (Help) – эта кнопка выводит контекстно-чувствительную справку. При щелчке на ней открывается окно справки, содержащее сведения о текущем диалоговом окне. -Кнопки, открывающие вспомогательные диалоговые окна: 1. Статистика (Statistics…) – отбираются показатели (статистики), которые будут выданы в результате расчета регрессии. К ним можно отнести: коэффициенты регрессии; данные по отклонениям от рассчитанной регрессии (остатки); набор показателей, характеризующих рассчитанную регрессию. 2. Графики (plots). 3. Параметры (Options) – позволяет задать определенные настройки для расчета регрессии, а именно: - критерий шагового метода (stepping method criteria), применяемые для отбора переменных при добавлении, исключении или шаговом методе; - включить в уравнение константу (include constant in equation), по умолчанию регрессионная модель содержит свободный член – константу. - различные варианты отношения к пропущенным значениям (исключать целиком (exclude cases listwise), исключать попарно (exclude cases pairwise), заменить средним (replace with mean)). |
Шаг 3. Выделите переменную y (время на 1 место проверки) в списке исходных переменных.
Шаг 4. Щелкните на кнопку 
и перенесите переменную в поле для зависимых переменных (Зависимая (Dependent)) 
Шаг 5. Выделите переменную x (количество концов проводов в месте проверки) в списке исходных данных
Шаг 6. Щелкните на кнопку и перенесите переменную в поле для независимых переменных (Независимая (Independent)) 
Шаг 7. Ничего больше не меняя, подтвердите операцию, щелкнув на кнопке 
. Результаты будут отображены в окне просмотра: SPSS Просмотрщик (SPSS Viewer).
В редакторе синтаксиса все проделанные выше действия будут представлены в следующем виде:
| REGRESSION * регрессия без параметров, значит включаются все данные /MISSING LISTWISE * /STATISTICS COEFF OUTS R ANOVA /CRITERIA=PIN(.05) POUT(.10) /NOORIGIN *присутствует свободный коэффициент (включить в уравнение константу); ORIGN – свободный коэффициент отсутствует. /DEPENDENT y - зависимая переменная /METHOD=ENTER * используемый метод. |
Окно просмотра (рис. 4) разделено на две части. В левой части отображается структура вывода, а в правой – собственно выводимые данные.
Рис.4 Структура документа вывода (Окно просмотра)
Рис. 5 Примечание
Далее приводится таблица (рис. 6) имеющая вспомогательное значение и актуальна для построения множественной регрессии. Здесь показывается порядок подбора (введение исключения) независимых переменных в процессе определения коэффициентов регрессии.
Рис. 6 Данные для построения множественной регрессии
Таблицы на рис. 7 и 8 имеют непосредственное отношение к оценке качества полученной регрессии. Величина R представляет собой оценку множественного коэффициента или индекса корреляции. Если имеется всего одна независимая переменная (как в данном случае), то множественный коэффициент корреляции R рассматривается просто как показатель корреляции между зависимой и независимой переменной. Если имеется несколько независимых переменных, то множественный коэффициент корреляции R является показателем корреляции между зависимой переменной и оптимальной линейной комбинацией независимых переменных (то есть характеризует предсказание зависимой переменной). Таким образом, чем ближе R к единице, тем лучше подгонка или соответствие модели данным.
Квадрат коэффициента корреляции R называется коэффициентом детерминации и показывает долю изменений (вариации) результативного признака под действием факторного признака. Чем ближе R2 к единице, тем лучше регрессия описывает связь между зависимой и независимой переменной. В нашем примере R2 равен
Эта величина характеризует качество регрессионной прямой, то есть степень соответствия между регрессионной моделью и исходными данными; это означает, что фактором «количество концов проводов на месте поверки» можно объяснить 100% «времени на одно место проверки».
Рис.7 Таблица со значениями R2 и скорректированного R2
Рис.8 Таблица с коэффициентами регрессионной модели
Рис.9 Таблица со значениями регрессии
Величина «смещенный R-квадрат (Adjusted R Square)» всегда меньше чем несмещенный (см. рис.7). При наличии большого количества независимых переменных, мера определенности корректируется в сторону уменьшения. Принципиальный вопрос о том, может ли вообще имеющаяся связь между переменными рассматриваться как линейная, проще и нагляднее всего решать, глядя на соответствующую диаграмму рассеяния (см. шаг 8).
Таблица на рис. 9 содержит собственно коэффициенты регрессионной модели – как ненормированные, так и нормированные. В последнем случае предполагается, что нормированное уравнение регрессии проходит через начало координат, поэтому константа отсутствует.
То есть уравнение регрессии выглядит следующим образом:
,
где коэффициент а=0.067, b=0.014 (см. табл. 9)
Для оценки статистической значимости коэффициентов регрессии рассчитываются t- критерий Стьюдента и доверительные интервалы каждого из коэффициентов. Выдвигается нулевая гипотеза о случайной природе коэффициентов, то есть о их незначимом отличии от нуля. Сравнивая фактическое (t) и критическое (табличное) значения (Знч.), принимаем или отвергаем нулевую гипотезу. Если Знч.<t, нулевая гипотеза отклоняется, то есть отличия коэффициентов от нуля не случайны. Если наоборот, Знч.>t, то нулевая гипотеза не отклоняется, и признается случайная природа формирования коэффициентов регрессии. Как следует из таблицы на рис.8, нулевая гипотеза отвергается для коэффициента при переменной, который признается случайной величиной, но его отличие от нуля считается статистически значимым.
Шаг 8. Теперь посмотрим, какие графические возможности предусмотрены программой для парной линейной регрессии. SPSS позволяет получить график регрессионной прямой с нанесением на нее облака рассеяния точек.
Выберите в меню следующие опции Графы (Graphs) –Разброс (Scatter plots или Scatter/Dot). Откроется диалоговое окно Разброс (Scatter plots или Scatter Dot) ( см. рис.), в которой нужно выбрать позицию Простой (Simple Scatter), а затем – Определить (Define).
Рис. 10 Диалоговое окно Диаграмма рассеяния ((Scatter plots или Scatter/Dot))
Откроется диалоговое окно Простая диаграмма рассеяния (Simple Scatter plot) (см. рис. 11)
Рис. 11 Диалоговое окно Простая диаграмма рассеяния (Simple Scatter plot)
Зададим оси Y (переменная «Время на 1 место проверки» (у)) и X («Количество концов проводов в месте проверки») и нажмем кнопку ОК.
В окне просмотра результатов мы получим диаграмму, представляющую собой облако рассеяния исходного множества точек, для которых необходимо построить линию регрессии (см. рис. 12) (напомним, что в этом задании мы имеем в виду парную линейную регрессию).
Рис. 12 Диаграмма с облаком рассеяния исходного множества точек
В редакторе синтаксиса проделанные выше действия (шаг 8) будут представлены в следующем виде:
GRAPH
/SCATTERPLOT(BIVAR)=x WITH y
/MISSING=LISTWISE.
Шаг 9. Щелкните дважды левой кнопкой мыши на этом графике. Появится окно SPSS Редактор диаграмм (Chart Editor).
Выберите в редакторе диаграмм меню Диаграмма (Chart) – Параметры (Options), откроется диалоговое окно Опции разброса (см. рис. 13).
Рис. 13 Диалоговое окно: Опции разброса
В рубрике Опции разброса (Fit Line) поставьте флажок напротив опции Total (Всего) щелкните на кнопке Fit Options (Опции закрепления). Откроется диалоговое окно Опции разброса: закрепить линию (Scatterplot Options: Fit line) (рис. 14).
Рис. 14 Диалоговое окно: «Опции разброса: Закрепить линию»
Подтвердите предварительную установку Линейная регрессия (Linear Regression) щелчком ОК (Continue) и затем ОК.
Закройте редактор диаграмм и щелкните один раз где-нибудь вне графика.
Шаг 10. На основе полученного регрессионного уравнения заполним таблицу данных, введя новую переменную, т.е. получим фактические значения.
Выберите в меню команды Трансформация (Transform) – Вычислить (Compute) откроется диалоговое окно Вычислить переменную (Compute Variable) (рис. 15):
Рис.15 Диалоговое окно Вычислить переменную (Compute Variable)
В поле Целевая переменная (Target Variable) указывается имя переменной, которой присваивается вычисляемое значение. В качестве целевой переменной может выступать как существующая переменная, так и новая. Вводим название новой переменной y1 в поле Целевая переменная (Target Variable). Далее щелкните на кнопке Тип и метка (Type&Label) и укажите метку и ее тип (см. рис. 16). В нашем случае в качестве метки в поле Метка (Label) мы указали Время на 1 место проверки, мин (фактическое). Новая переменная (y1) будет содержать числовые значения, поэтому мы выбрали тип Цифровой (Numeric). Далее нажмите кнопку Продолжение (Continue) (см. рис. 19).
Рис.16 Диалоговое окно: Type and Label
После определения новой переменной в области Числовое выражение (Numeric Expression) следует указать непосредственно рассчитываемое значение. Компоненты сконструированного выражения, в данном случае регрессионной зависимости, могут быть вставлены в поле Числовое выражение (Numeric Expression) или введены туда с клавиатуры. Заносим полученное регрессионное уравнение 
(см. рис. 17)
Шаг 11. Ничего больше не меняя, подтвердите операцию, щелкнув на кнопке . В окне SPSS Data Editor появится новая переменная (см. рис. 17)
Рис. 17 Окно Редактор данных SPSS с вкладкой Панель данных (Data View)
Шаг 12. Кроме проведенного регрессионного анализа возможно проверить абсолютные и относительные отклонения полученных фактических величин (y1) от нормативных (y).
Для этого создаем 2 переменные: abs – абсолютные отклонения и otn – относительные отклонения.
;
.
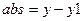Выполняем все действия в соответствии с шагом 10.
В результате получится следующая таблица (см. рис. 18):
Рис.18 Окно Редактор данных SPSS с вкладкой Панель данных (Data View)
В окне просмотра данных полученные полученный результат можно представить в более наглядном виде.
1. Выберите в меню команды Анализ (Analyze) – Отчеты (Reports) – Итоги регистров (Case summaries), откроется диалоговое окно Итоги регистров (Summarize cases) (см. рис)
Рис. 19. Диалоговое окно: Итоги регистров
Перенесите все переменные из списка исходных переменных в список выбранных переменных Переменные (Variables). Отмете галочкой Показ регистров (Display cases). Нажмите кнопку Параметры (Options) – откроется диалоговое окно Параметры (Options) (см. рис. 20)
Рис.20 Диалоговое окно: Параметры (Options)
В поле Заголовок (Title) введите название таблицы и нажмите кнопку Продолжение (Continue).
3.Подтвердите операцию щелкнув на кнопке ОК.
В окне просмотрщика SPSS появится итоговая таблица (см. рис. 21)
Рис.21 Итоговые значения
В соответствии с полученными данными можно утверждать, что отклонения фактических результатов (на основе уравнения регрессии) от нормативных лежат в допустимых пределах (до 10%) – максимальное относительное отклонение 1,72 % (0,0172).
Подгонка кривых
Регрессия, парная или множественная, совсем не обязательно должна быть линейной. Существует много других, нелинейных, форм для её выражения, хотя большинство нелинейных форм возможно при помощи соответствующих трансформаций можно перевести в линейную модель. В SPSS для формирования нелинейной регрессии предусмотрены следующие технологии:
-подгонка кривых;
-использование фиктивных переменных;
-собственно нелинейная регрессия.
Подгонка кривых
Подгонка кривых (Curve Estimation) предназначена, В первую очередь, для вычисления парной нелинейной регрессии. Эта процедура позволяет вычислять статистики и строить графики для различных типовых регрессионных моделей. Можно также сохранять предсказанные значения, остатки и интервалы прогнозирования в виде новых переменных.
Шаг 1. Заносим данные в SPSS.
Таблица 2
Зачистка наружных поверхностей деталей
| Длина зачищаемой поверхности, мм до: | Диаметр или ширина поверхности, мм, до: |
| 0,18 | |
| 0,2 | |
| 0,24 | |
| 0,26 | |
| 0,29 | |
| 0,33 | |
| 0,37 | |
| 0,41 | |
| 0,45 | |
| 0,49 | |
| 0,53 | |
| 0,58 | |
| 0,62 |
Находим однофакторную парную регрессию. За независимую переменную примем - «Длину зачищаемой поверхности» (L), за зависимую – «Штучно калькуляционное время» (t).
Шаг2. Прежде чем запустить выполнение процедуры, полезно ознакомиться с расположением исходных точек на графике, чтобы определить наиболее подходящие кривые, но с использованием данной процедуры это действие не всегда является обязательным.
Теперь обратимся к процедуре подгонка кривых, для чего выполним последовательность команд Анализ (Analyze) – Регрессия (Regression) – Оценка кривой (Curve Estimation).
Открывается диалоговое окно Оценка кривой (Curve Estimation), в котором можно выбрать одну из одиннадцати моделей (см. рис. 22).
Рис.22 Диалоговое окно: Оценка кривой (Curve Estimation)
Предлагаемые модели соответствуют следующим типам (выражаемым посредством формул) – см. табл. 3
Таблица 3
Типы моделей
| Модель | Формула |
| Линейная (Linear) | 
|
| Логарифмическая (Logarithmic) | 
|
| Обратная (гиперболическая) (Inverse) | 
|
| Квадратичная (Quadratic) | 
|
| Кубическая (Cubic) | 
|
| Степенная (Power) - Питание |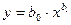 
|
| Показательная (Compound) - Компоунд | 
|
| S | 
|
| Логистическая (Logistic) | 
|
| Рост (Growth) | 
|
| Экспоненциальная (Exponential) |  
|
Шаг3.. щелкните на кнопку и перенесите переменную в поле для зависимых переменных (Зависимая (Dependent)) 
.
Шаг 4. Щелкните на кнопку и перенесите переменную L (Длина зачищаемой поверхности) в поле 
для независимых переменных (Независимая (Independent))
Шаг 5. В диалоговом окне Оценка кривой (Curve Estimation) активизируем отобранные модели (Модели (Models)) - линейную, квадратичную, кубическую, степенную, показательную и экспоненциальную. Кроме того, установим флажки в ячейках Включить в уравнение (Include constant in equation), Модели точек (Plot models). В результате получатся графики отобранных функций и, дополнительно, график аппроксимации наблюдаемых значений.
Шаг 6. Подтвердите операцию, щелкнув на кнопке ОК.
Вывод результатов производится в старой табличной форме (см. пример1.) Самыми важными показателями являются (см. рис.23):
MODEL: MOD_1.
Independent: L
Dependent Mth Rsq d.f. F Sigf b0 b1 b2 b3
T LIN,956 11 239,17,000,2091,0043
T QUA,994 10 773,80,000,1628,0075 -3,E-05
T CUB,998 9 1456,53,000,1391,0103 -1,E-04 4,0E-07
T COM,867 11 71,69,000,2244 1,0116
T POW,999 11 13718,9,000,0920,4098
T EXP,867 11 71,69,000,2244,0115
Рис. 23 Коэффициенты регрессии
Эта таблица содержит значения коэффициентов b0, b1, b2, b3.
Далее в окне просмотра появляется график, на котором отображаются кривые, соответствующие изменению наблюдаемых значений (см. рис. 24):
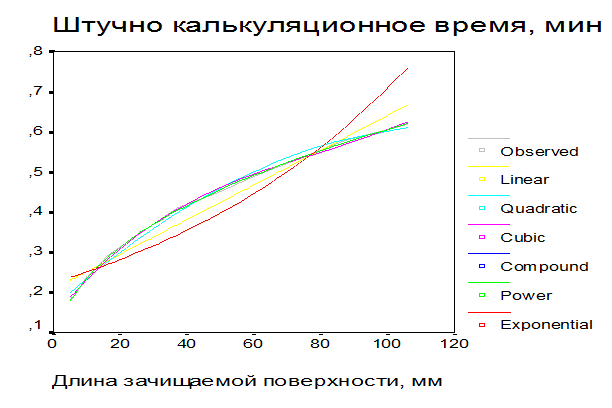
Рис. 24 Наблюдаемая и оценочные кривые
Сравнение всех этих кривых показывает, что наилучшее приближение к множеству исходных точек дает степенная модель: 
.
Оснований для такого утверждения два:
1. это видно из подобия кривых степенной модели и реальных значений (рис. (кривые));
2. данный вывод подтверждается результатами анализа для степенной модели (Рис. (коэффициенты)), согласно которым R2=0.999, что говорит о хорошем приближении
Если установим флажок в ячейку Показ таблицы ANOVA (Display ANOVA table) (для фиксации оценок качества регрессии) (см. рис.22), то будет выведен подробный анализ по каждой зависимости отдельно (см. рис 25):
Рис. 19 Дисперсионный анализ линейной модели
В редакторе синтаксиса проделанные выше действия (до 6 шага) будут представлены в следующем виде:
| *подгонка гривых * Curve Estimation. TSET NEWVAR=NONE. CURVEFIT /VARIABLES=t WITH L /CONSTANT /MODEL=LINEAR QUADRATIC CUBIC COMPOUND POWER EXPONENTIAL /PRINT ANOVA /PLOT FIT. | запуск функции; 2 переменные t=f(L) (Включить константу) выбранные модели; дисперсионный анализ; выводим график зависимостей; |
Шаг 7. Вывод в соответствии с шагом 12 линейной регрессии..
Задание: Находим однофакторную парную регрессию. За независимую переменную примем - «Длину зачищаемой поверхности» (l), за зависимую – «Штучно калькуляционное время» (t)
4. Нелинейная регрессия
Многие связи по своей природе, то есть в реальной жизни, либо являются строго линейными, либо их можно привести к линейному виду. Один пример линейно связи рассмотрели. Гораздо более сложной становится ситуация, когда нелинейная функция не поддается линеаризации. В этом случае параметры могут быть определенны лишь итеративным путем посредством последовательных приближений в процессе нелинейной оптимизации, когда минимизируется сумма квадратов разностей между предсказанными значениями регрессии по подбираемой формуле и исходным значениям. Здесь решающим значением становится подбор функциональной формы регрессионной модели, а также определение начальных значений искомых коэффициентов для нулевой итерации. Даже если выбрана подходящая формула, неудачное значение может привести к тому, что итерационный процесс вообще не сойдется, или к тому, что полученное решение будет локальным, то есть годным лишь для конкретной точки и её окрестностей. В общем случае при этом варианте расчета предусматривается достаточно длинный, многоступенчатый процесс.
Шаг 1. Заносим данные в SPSS (см. таблицу 2).
Таблица 4