Действие с обыкновенными дробями
1) Чтобы выделить целую часть из неправильной дроби нужно числитель разделить на знаменатель, неполное частное будет целой частью, остаток – числителем, а знаменатель останется тем же.
Пример: Выделить целую часть из неправильной дроби: 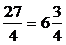 , т.к. 27: 4=6 остаток 3. , т.к. 27: 4=6 остаток 3.
|
2) Чтобы записать смешанное число в виде неправильной дроби нужно целую часть умножить на знаменатель и прибавить числитель, полученное число записать в числитель, а знаменатель оставить тем же.
Пример: Записать смешанное число в виде неправильной дроби: 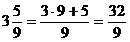
|
3) Сократить дробь, это значит разделить числитель и знаменатель на одно и то же число неравное нулю.
Пример: Сократить дробь: 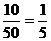
|
Чтобы сложить дроби с разными знаменателями нужно
1. привести дроби к наименьшему общему знаменателю (т.е. найти такое число, которое делится на знаменатель первой дроби и на знаменатель второй дроби без остатка),
2. найти дополнительный множитель для каждой дроби (т.е. разделить общий знаменатель на знаменатель первой дроби и на знаменатель второй дроби),
3. умножить дополнительный множитель на числитель первой дроби и на числитель второй дроби, это будет числитель первой дроби, и числитель второй дроби,
4. полученные числители сложить,
5. записать общий знаменатель,
6. если можно сократи,
7. если можно выдели целую часть.
4) 
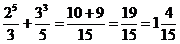
5) 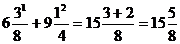
6) 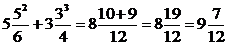
7) 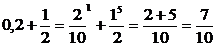 или
или 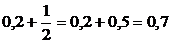
Чтобы вычесть дроби с разными знаменателями нужно
1. привести дроби к наименьшему общему знаменателю (т.е. найти такое число, которое делится на знаменатель первой дроби и на знаменатель второй дроби без остатка),
2. найти дополнительный множитель для каждой дроби (т.е. разделить общий знаменатель на знаменатель первой дроби и на знаменатель второй дроби),
3. умножить дополнительный множитель на числитель первой дроби и на числитель второй дроби, это будет числитель первой дроби, и числитель второй дроби,
4. полученные числители вычесть,
5. записать общий знаменатель,
6. если можно сократи,
7. если можно выдели целую часть.
8) 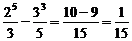
9) 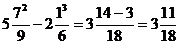
10) 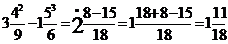
11) 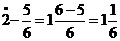
12) 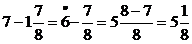
Чтобы умножить дробь на дробь нужно числители перемножить и знаменатели перемножить. Если можно сократи, если можно выдели целую часть.
13) 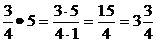
14) 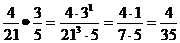
15) 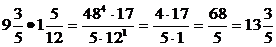
16) 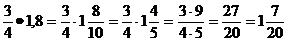 или
или 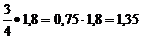
17) Чтобы разделить дробь на дробь делимое умножить на число обратное делителю (т.е. деление заменить умножением, перевернуть вторую дробь). Если можно сократи, если можно выдели целую часть.
18) 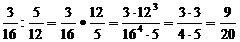
19) 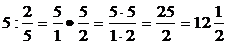
20) 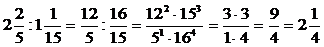
21) Найти часть от числа.Найти 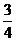 от 12. 12
от 12. 12 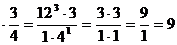
22) Найти число по его части. Найдите число 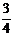 , которого равны 12.
, которого равны 12. 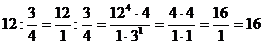
Действие с положительными и отрицательными числами
1) Пол. + пол. = пол.
2) Отр. + отр. = отр.
Чтобы сложить отрицательные числа нужно поставить знак минус и модули чисел сложить.
3) Пол. + отр. = знак большего модуля и из большего модуля вычесть меньший.
Чтобы сложить два числа с разными знаками нужно, поставить знак большего модуля и из большего модуля вычесть меньший.
4) + · + = +
5) ¾ · ¾ = +
Чтобы умножить два числа с одинаковыми знаками нужно, поставить знак + и модули множителей перемножить.
6) ¾ · + = ¾
Чтобы умножить два числа с разными знаками нужно, поставить знак - и модули множителей перемножить.
7) +: + = +
8) ¾: ¾ = +
Чтобы разделить два числа с одинаковыми знаками, нужно поставить знак + и модули разделить.
9) ¾: + = ¾
Чтобы разделить два числа с разными знаками, нужно поставить знак - и модули разделить
Раскрытие скобок
1) Если перед скобками или после скобок стоит знак умножения, то скобки раскрываются «фонтанчиком».
2·(3а – 5) = 6а - 10
2) Если перед скобками стоит знак плюс то, раскрывая скобки, знаки слагаемых оставляют без изменения.
5+(а – в) = 5 + а - в
3) Если перед скобками стоит знак минус, то, раскрывая скобки, знаки слагаемых меняют на противоположные.
5 - (а – в) = 5 - а + в
Подобные слагаемые
1) Слагаемые называются подобными, если имеют одинаковую буквенную часть. 4у, 34у, -5у, 2,5у.
2) Чтобы привести подобные слагаемые нужно их коэффициенты сложить, а буквенную часть приписать.
3) у- 3х- 5х + 8 - 12у = - 8х - 11у + 8 (-8х и -11у не подобные, для 8 нет подобных)