Пусть события А1 , А2, …, Аn независимы в совокупности, причем вероятности Р (А1)=р1 , Р (А2)=р2 , …, Р (Аn)=рn ; пусть в результате испытания могут наступить все события, либо часть из них, либо ни одно из них.
Вероятность наступления события А, состоящего в появлении хотя бы одного из событий
А1 , А2, …, Аn , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий А1 , А2, …, Аn:
Р(А)=1 - q1 q2 … qn.
В частности, если все n событий имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий
Р(А)=1 – qn (*).
Задача 9. Вероятность попадания стрелком в мишень при одном выстреле 0,6. Найти вероятность того, что мишень будет поражена хотя бы один раз при трех выстрелах.
Решение. Вероятность поражения мишени при одном выстреле равна р = 0,6, а q = 1-0,6= 0,4.
Выстрела было произведено 3, т.е n = 3.
Искомая вероятность равна:
Р (А) = 1 – q3 = 1 – (0,4)3 = 1 – 0,064 = 0,936.
Ответ: Вероятность того, что мишень поражена хотя бы один раз при трех выстрелах равна 0,936.
Задача 10. Вероятность хотя бы одного попадания стрелком в мишень при четырех выстрелах равна 0,9984. Найти вероятность попадания при одном выстреле.
Решение. Вероятность попадания в мишень хотя бы при одном из четырех выстрелов (событие А) равна
Р (А) = 1 – q4,
где q – вероятность промаха.
По условию Р (А) = 0,9984.
Следовательно, 0,9984 = 1 - q4, или q4 = 1 – 0,9984 = 0,016.
 Отсюда q = 4√0,0016 = 0,2.
Отсюда q = 4√0,0016 = 0,2.
Искомая вероятность
р = 1 – q = 1 – 0,2 = 0,8.
Ответ: Вероятность попадания в мишень при одном выстреле
равна 0,8.
ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ
Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) Н1 , Н2, …, Нn , образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на со ответ ствующую условную вероятность события А:
Р (А) =Р (Н1) ∙ Р (А /Н1) + Р (Н2) ∙ Р (А /Н2) + … + Р(Нn) ∙ Р (А /Нn) (*),
где Р (Н1) + Р (Н2) + … + Р(Нn) = 1.
Равенство (**) называют формулой полной вероятности.
Задача 11. В каждой из двух урн содержится по 5 черных и 3 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую. Найти вероятность того, что шар, извлеченный из второй урны окажется черным.
Решение. Урна1 Урна2
|
|
Переложим 1 шар

Проанализируем условие задачи, если из урны 1 переложим белый или черный шар в урну 2 (см. схему).
Запишем условие задачи в схеме.
Урна №1
| 5(Б) | 3(Ч) | |
 8 шаров 8 шаров
|
|
 |  |
Урна №2 Урна №2
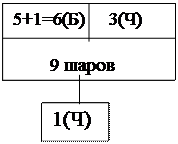 | 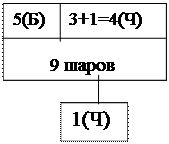 |
Обозначим через А событие – извлеченный из второй урны шар окажется черным. Возможны следующие предположения (гипотезы):
Н1 – из I урны вынут белый шар, Р (Н1) = 5/8;
Н2 -из I урны вынут черный шар, Р (Н2 ) = 3/8 (P (Н1)+ (Н2)=1).
Условная вероятность того, что извлеченный из II урны шар черный при условии, что белый шар из I урны переложен во вторую, Р (А/Н1) = 3/ 9.
Условная вероятность того, что извлеченный из II урны шар белый при условии, что черный шар из I урны переложен во вторую,
Р (А/Н1) = 4/ 9.
Искомая вероятность того, что извлеченный из второй урны, шар окажется черным по формуле полной вероятности:
Р (А) =Р (Н1) ∙ Р (А /Н1) + Р (Н2) ∙ Р (А /Н2) = 5/8· 3/ 9 + 3/8· 4/9= =27/ 72= 3/8
Ответ: Вероятность того, что шар, извлеченный из второй урны окажется черным равна 3/8.
ФОРМУЛА БЕЙЕСА
Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) Н1, Н2, … Нn, которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формуле Бейеса:
Р (Нi /А) = Р (Н1) · Р (А/Н1) (i=1,2,…, n),
Р (А)
где Р (А) – формула полной вероятности.
Задача 12. Две перфораторщицы набили по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,2; для второй перфораторщицы эта вероятность равна 0,3. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась вторая перфораторщица.
Решение. Обозначим через А событие – обнаружена ошибка в перфокарте. Можно сделать два предположения (гипотезы).
Н1 – набивала перфокарты перфораторщица №1
Н2 – набивала перфокарты перфораторщица №2. Поскольку имеется две гипотезы, причем по условию они равновероятны, и сумма вероятностей гипотез равна единице
Р(Н1) = Р(Н2) = ½, то (Р(Н1) + Р(Н2) = 1)
Условная вероятность того, что первая перфораторщица допустила ошибку:
Р (А/Н1) = 0,2, а вторая – Р (А/Н2) = 0,3.
Вероятность, что при сверке перфокарт была допущена ошибка, находим по формуле полной вероятности:
Р (А) =Р (Н1) ∙ Р (А /Н1 + Р (Н2) ∙ Р (А /Н2) = 1/2· 0,2+ 1/2 · 0,3 = 0,25.
Искомая вероятность того, что ошиблась вторая перфораторщица, по формуле Бейеса равна:
Р (Н2 /А) = Р (Н2) · Р (А/Н2) = 0,15 = 3.
Р (А) 0,25 5
Ответ: Вероятность того, что ошиблась вторая перфораторщика равна 3/5.
ФОРМУЛА БЕРНУЛЛИ
7.1. Если производятся испытания, при которых вероятность появления события А в каждом из них не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
7.2 Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0<р<1), событие наступит ровно k раз (безразлично, в какой последовательности), равна
Рn (k) = C kn pk qn - k,
или
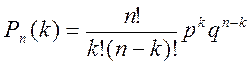 ,
,
где q = 1 – p.
7.3 Вероятность того, что в n испытаниях событие наступит: а) менее k раз; б) более k раз; в) не менее k раз; г) не более k раз, находят соответственно по формулам:
а) Рn (0) + Рn (1) + … + Рn (k - 1);
б) Рn (k + 1) + Рn (k + 2) + … + Рn (n);
в) Рn (k) + Рn (k + 1) + … + Рn (n);
г) Рn (0) + Рn (1) + … + Рn (k).
Задача 13. Монету бросают пять раз. Найти вероятность того, что “герб” выпадет:
а) ровно два раза;
б) менее двух раз;
в) не менее двух раз.
Решение. Вероятность того, что выпадет “герб” р = 0.5, не “герб” 0,5(q = 1 – 0,5 = 0.5). Монету бросают пять раз, значит, n = 5.
Применим формулу Бернулли:
а) найдем вероятность того, что «герб» выпадает два раза при пяти бросаниях монеты:
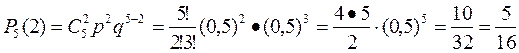 ;
;
б) найдем вероятность того, что «герб» выпадает менее двух раз при пяти бросаниях монеты:
P5 (k <2) = P5 (0) + P5 (1) =  ;
;
в) найдем вероятность того, что «герб» выпадает не менее двух раз. События «герб» выпадает менее двух раз и «герб» выпадает не менее двух раз противоположны:
Р5 (k ≥ 2) = 1 - P5 (k <2) = 1 – 3/16 = 13/16.
Ответ: Вероятность, что герб выпадает ровно два раза - 5/16, менее двух раз - 3/16, не менее двух раз - 13/16.
Задача 14. Вероятность хотя бы одного попадания при двух выстрелах равна 0,84. Найти вероятность четырех попаданий при пяти выстрелах.
Решение. По формуле появления хотя бы одного события имеем:
Р = 1 – q2 = 0.84, q2 = 0,16, q = 0,4, р = 1 – q = 0,6.
Искомая вероятность четырех попаданий при пяти выстрелах по формуле Бернулли равна:
 .
.
Ответ: Вероятность четырех попаданий при пяти выстрелах
равна 162
625.