РЕАКЦИЯ ЛИНЕЙНОЙ СИСТЕМЫНА ДЕЛЬТА-ФУНКЦИЮ ДИРАКА. СВЕРТКА
Содержание
1. Разложение сигналов по единичным импульсам. Единичные импульсы. Разложение сигнала. Импульсный отклик линейной системы.
2. Интеграл Дюамеля.
3. Свертка (конволюция) сигналов. Интеграл свертки.
Введение
Можно выделить два основных метода анализа переходных процессов, возникающих при прохождении сигналов через линейные инвариантные во времени системы (ЛИВС):
1. Спектральный метод (преобразование Фурье или Лапласа), использующий частотную форму представления сигналов.
2. Суперпозиционный метод, основанный на динамическом представлении сигнала как суперпозиции элементарных импульсов некоторой «стандартной» формы.
Динамическая форма представления сигналов соответствует естественному и привычному для нас математическому описанию в виде функций независимых переменных (аргументов) в реальном (текущем) масштабе времени. Динамические модели сигналов позволяют определять текущие значения сигналов в любых системах по заданным математическим функциям описания физических процессов в реальных физических системах или системных операций в программных системах. Достоинством динамических моделей является их универсальность. Основные математические инструменты реализации - дифференциальные уравнения и интеграл Дюамеля, для цифровых сигналов - разностные уравнения и операция свертки.
Основной задачей динамической модели является математическое описание реакции системы (выходного сигнала системы) на определенное входное воздействие (входной сигнал). Моделирование и анализ линейных стационарных систем обработки сигналов произвольной формы в динамическом представлении базируется на разложении сигналов по единичным импульсам простейшей формы.
Разложение сигналов по единичным импульсам
Единичные импульсы. В качестве математической модели единичного импульса при анализе аналоговых сигналов используют дельта-функцию.
Дельта-функция или функция Дирака. По определению, дельта-функция описывается следующим математическим выражением:
d(t-t) = 0 при t ¹ t, 
d(t-t) dt = 1.
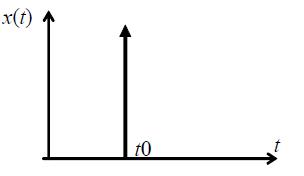
Рис 1.сигнал в виде дельта-функции
Функция d(t-t) не является дифференцируемой, и имеет размерность, обратную размерности ее аргумента, что непосредственно следует из безразмерности результата интегрирования. Значение дельта-функции равно нулю везде за исключением точки t, где она представляет собой бесконечно короткий импульс с бесконечно большой амплитудой, при этом площадь импульса равна 1.
Дельта-функция является полезной математической абстракцией. На практике такие функции не могут быть реализованы с абсолютной точностью, так как невозможно реализовать значение, равное бесконечности, в точке t = t на аналоговой временной шкале, определенной по времени также с бесконечной точностью. Но во всех случаях, когда площадь импульса равна 1, длительность импульса достаточно мала, а за время его действия на входе какой-либо системы сигнал на ее выходе практически не изменяется (реакция системы на импульс во много раз больше длительности самого импульса), входной сигнал можно считать единичной импульсной функцией со свойствами дельта - функции.
Математическое выражения d(t-t) называют также импульсом Дирака. Однако, применяя такую терминологию, не следует забывать, что это не просто единичные импульсы в координатных точках t, а импульсные функции, определяющие как значения импульсов в определенных координатных точках, так и нулевые значения по всем остальным координатам, в пределе от -¥ до ¥.
Разложение сигнала по единичным импульсам. Импульсы Дирака используются для разложения, соответственно, произвольных аналоговых сигналов s(t) в непрерывную последовательность неперекрывающихся (ортогональных) импульсов:
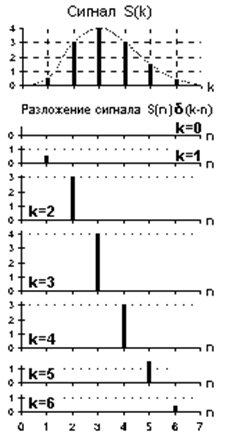Рис. 2
|
s(t) = s(t)d(t-t) dt. (2)
Для аналоговых сигналов разложение (2) в физическом представлении эквивалентно сканированию значений сигнала s(t) в моменты времени t = t бесконечно узкой щелью, бегущей вдоль оси t. Другими словами, единичные импульсные функции d(t-t), -¥<t< ¥, образуют в бесконечномерных пространствах системы координатных базисов {d(t-t)}, т.к. они не перекрываются и, соответственно, взаимно ортогональны. По этим координатным системам и производится разложение сигнала s(t).
Так, например, простейшая система базисных векторов в N-мерном пространстве задается единичной матрицей порядка N, т. е. диагональной матрицей размера N x N с единичными диагональными элементами. Каждая строка этой матрицы соответствует единичному импульсу, смещенному на k позиций:
Любые две строки матрицы ортогональны
,
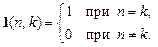а норма базисной функции равна 1:
.
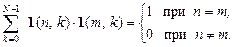Выражение (2) представляет собой совокупность проекций сигналов на координатные базисы систем единичных импульсов и является векторным описанием сигналов в динамической форме.
Импульсный отклик линейной системы. Если на вход линейной системы в момент времени t = 0 подать единичный импульс Дирака, то на выходе мы получим реакцию системы на единичный входной сигнал. Эта реакция называется функцией импульсного отклика системы или импульсной характеристикой. Она однозначно определяется оператором преобразования h(..):
y(t) = T[d(t-0)] = h(t). (3)
Импульсный отклик аналоговой системы на входную дельта-функцию также в определенной степени представляет собой математическую абстракцию идеального преобразования. С практической точки зрения под импульсным откликом можно понимать отображение реакции системы на импульсный входной сигнал произвольной формы с единичной площадью, если длительность этого сигнала пренебрежимо мала по сравнению с временной (координатной) разрешающей способностью системы. Функцию импульсного отклика называют также весовой функцией системы.
Очевидно, что в линейных и инвариантных к сдвигу системах форма импульсного отклика не зависит от времени прихода входного сигнала и определяет только его положение на временной оси. Так, если входной импульс задержан (относительно 0) на время to, то соответствующий выходной сигнал будет определяться выражением:
y(t) = T[d(t-to)] = h(t-to).
В любой системе, работающей в реальном масштабе времени, сигнала на выходе системы не может быть, если нет сигнала на ее входе. Отсюда следует односторонность импульсного отклика физических систем:
h(t-t) = 0 при t<t.
Условно процесс для коротких входных импульсных сигналов может быть представлен в следующем виде. Для любой точки расчета ti выходного сигнала инвертированная по координатному направлению функция импульсного отклика h(t) помещается в эту точку ti и просматривается по своей координате t с одновременным синхронным просмотром входного сигнала s(t) назад от точки расчета по координатам ti-t. Значения всех встреченных при просмотре импульсов s(ti-t) перемножаются со значениями h(t) и суммируются. Тем самым, для каждой текущей точки расчета ti в аналоговой системе выполняется операция:
y(ti) =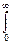 
h(t)×s(ti-t) dt. (5)
Результат выражений (5) и будет представлять собой запаздывающую реакцию системы на все импульсы, поступившие на вход системы до текущей точки расчета выходного сигнала.
Таким образом, для линейных и стационарных систем легко определить их реакцию на любой входной сигнал, если известен импульсный отклик систем на единичный входной сигнал.
Интеграл дюамеля
Произвольный аналоговый сигнал s(t) можно представить в дискретной форме с шагом Dt в виде ступенчатой функций с высотой каждой ступеньки, равной приращению функции s(t) между соседними точками (рис. 3):
s(t) ≈ s(0)s(t)+(s1-s0)s(t-Dt)+(s2-s1)s(t-2Dt)+…= s(0)s(t) +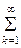 
(sk-sk-1)s(t-kDt).
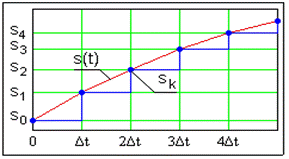Рис. 3
|
где s(t) – функция включения. В пределе, для бесконечно малого значения шага дискретизации:
Dt → t, (sk-sk-1) → ds = (ds/dt)dt, kDt → t,
получаем формулу динамического представления сигнала посредством функций включения:
s(t)= s(0)s(t) +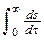 
s(t-t) dt.
Реакция системы на функцию включения s(t) называется её переходной характеристикой и обозначается через g(t). Для линейной системы с переходной характеристикой g(t) входное воздействие s(t-t) вызывает отклик g(t-t), поэтому
s(t) Þ s(0)s(t) + 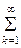(sk-sk-1)g(t-kDt).
Переходя к переделу при Dt → 0, получим выражение, которое называют интегралом Дюамеля:
y(t)= s(0)s(t) +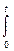 
s’(t)g(t-t) dt, (3.2.1)
Тождественная форма:
y(t)= s(0)s(t) + 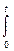s’(t-t)g(t) dt, (3.2.1’)
Интеграл Дюамеля целесообразно применять, когда известна или легко находится переходная характеристика системы.
Рис. 4
|
Пример расчета выходного сигнала системы на ступенчатый входной сигнал приведен на рис. 4 Ступенчатая форма сигнала принята для более наглядного представления процесса формирования выходного сигнала. В общем случае, форма входного воздействия может быть произвольной.