Задание 1
Соединение «звездой» в трёхфазной сети
I Графоаналитический метод
1 Определяем полные сопротивления каждой фазы по формулам:
,
,
2. Определяем фазное напряжение по формуле:
,
3. Рассчитаем токи в каждой фазе по формулам:
,
,
4. Определяем сдвиг фаз по формулам:
,
,
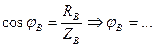При определении 
использовать таблицу тригометрических функций (Приложение 6: Евдокимов Ф.Е. «Теоретические основы электротехники»).
5. Для определения тока в нулевом проводе 
необходимо построить векторную диаграмму в масштабе в следующем порядке:
а) откладываем вектора фазных напряжений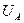 
, 
, 
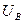в масштабе под углом 1200 относительно друг друга:
Рисунок 10
б) относительно векторов фазных напряжений откладываем вектора фазных токов в масштабе.
При этом необходимо помнить что:
- при активной нагрузке ток и напряжение совпадают по фазе;
- при индуктивной нагрузке ток отстаёт от напряжения на 900;
- при ёмкостной нагрузке ток опережает напряжение на 900;
- при активно-индуктивной нагрузке ток отстаёт от напряжения на какой-то угол 
;
- при активно-ёмкостной нагрузке ток опережает напряжение на какой-то угол 
;
в) складываем вектора фазных токов и находим ток в нулевом проводе.
II Символический метод
1. Записываем комплексы полных сопротивлений для каждой фазы по формулам:
,
,
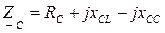
2. Определяем комплексы фазных напряжений по формулам:
,
,
,
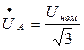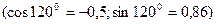
3.Рассчитаем комплексы фазных токов по формулам:
4.Определим ток в нулевом проводе по формуле:
5.Определим мощность в каждой фазе и потребляемую мощность по формулам:
где 
– сопряженный комплекс тока (меняется знак перед мнимой частью комплексного числа)
|
|
6. Изображаем фазные токи IA, IB, IC; ток в нулевом проводе I0 и фазные напряжения UA, UB, UC векторами на комплексной плоскости в масштабе:
на оси х – действительную часть;
на оси y – мнимую
Соединение «треугольником» в трехфазной сети
I Графоаналитический метод
1. Начертим схему при соединении треугольником.
2. Определим полные сопротивления каждой фазы:
(при соединении звездой)
(при соединении звездой)
(при соединении звездой)
3.Опеределяем фазное напряжение:
4.Рассчитаем токи в каждой фазе по формулам:
,
,
5.Определим сдвиги фаз между током и напряжением в каждой фазе по формулам:
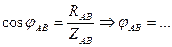
При определение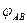 
, 
, 
использовать таблицу тригонометрических функций (Приложение 6: Евдокимов Ф.Е. «Теоретические основы электротехники»)
6.Строим векторную диаграмму присоединении в следующем порядке:
а) откладываем вектора фазных напряжений UAB, UBC, UCA в масштабе под углом 1200 относительно друг друга;
б) относительно векторов фазных напряжений откладываем вектора фазных токов в масштабе. При этом необходимо учитывать характер нагрузки в каждой фазе (как ведут себя ток и напряжение по отношению друг к другу);
в) определяем линейные токи по следующим уравнениям:
,
,
II Символический метод
1.Записываем комплексы полных сопротивлений для каждой фазы:
(при соединении звездой);
(при соединении звездой);
(при соединении звездой)
2.Определяем комплексы фазных напряжений по формулам:
,
,
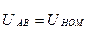(cos1200 = -0,5; sin1200 = 0,86)
|
|
3.Рассчитаем комплексы фазных токов по формулам:
,
,
,
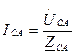4.Определим комплексы линейных токов по формулам:
,
,
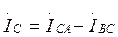
5.Определим мощность в каждой фазе и потребляемую мощность по формулам:
где 
– сопряженный комплекс тока (меняется знак перед мнимой частью комплексного числа).
6. Изображаем линейные токи IA, IB, IC; фазные токи IAB, IBC, ICA; фазные напряжения UAB, UBC, UCA векторами на комплексной плоскости в масштабе:
на оси х – действительную часть;
на оси у – мнимую