Дана нагрузка при соединении звездой
Рисунок 11
|
380 В
10 Ом
6 Ом
20 Ом
10 Ом
I Графоаналитический метод
1.Определим полные сопротивления каждой фазы:
Ом,
Ом,
Ом
2.Определим фазное напряжение:
3. Рассчитаем токи в каждой фазе:
A,
A,
A
4.Определим сдвиг фаз:
,
,
5.Строим векторную диаграмму
- выбираем масштаб:
М: по току: 1см – 4 А
По напряжению: 1см – 60 В
- откладываем вектора фазных напряжений в масштабе относительно друг друга под углом 1200: фазное напряжение равно 220 В, 220 делим на масштаб (60), получаем 3,7см (откладываем фазное напряжение по 3,7см каждое)
Рисунок 12
- откладываем вектора фазных токов в масштабе соответственно нагрузке:
В фазе А включена активно-индуктивная нагрузка Þфазный ток IА отстаёт от напряжения UА на угол сдвига фаз 
А, 18,8 делим на масштаб (4), получаем 4,7см (откладываем IA=4,7 см).
В фазе В включена активная нагрузка Þ фазный ток IB совпадает с напряжением UB по фазе: IB=11 А, 11 делим на масштаб (4), получаем 2,8 см (откладываем IB=2,8 см).
В фазе С включена емкостная нагрузка Þфазный ток IC опережает напряжение UC на угол сдвига фаз 
: 
А, 22 делим на масштаб (4), получаем 5,5 см (откладываем IC=5,5 см)
- складываем вектора фазных токов и находим ток в нулевом проводе:
измеряем получившийся вектор 
, 
умножаем на масштаб (4), получаем 30 А:
II Символический метод
1.Записываем комплексы полных сопротивлений для каждой фазы:
Ом
Ом
Ом
2.Определим комплексы фазных напряжений:
В
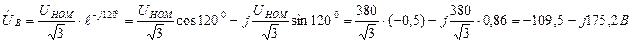
3.Рассчитаем комплексы фазных токов:
Находим модуль тока 
Находим модуль тока 
Находим модуль тока 
4.Определим ток в нулевом проводе:
5.Определим мощность в каждой фазе и потребляемую мощность:
|
|
, 
, 
, 
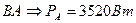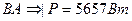
6. Изображаем вектора фазных токов и напряжений и ток в нулевом проводе векторами на комплексной плоскости
- выбираем масштаб: по току: 1см – 5А
по напряжению: 1 см – 50В
- откладываем вектор фазного тока IA
A
- 16 делим на масштаб (5), получаем 3,2 см, отмечаем 3,2см на действительной оси (+1);
- -9,7 делим на масштаб (5), получаем 1,94см, отмечаем 1,94см на мнимой оси (j).
Находим точку пересечений этих двух векторов, соединяем её с началом координат, получаем вектор тока IA.
Аналогичным образом откладываем вектор: 
.
Рисунок 13
Произведём в первоначальной схеме переключения со «звезды» на «треугольник».
Получим схему
Рисунок 14
I Графоаналитический метод
1. Определяем полные сопротивления каждой фазы:
2. Определяем фазное напряжение:
3. Рассчитаем токи в каждой фазе:
A,
А,
А,
4. Определим сдвиги фаз:
,
,
5. Строим векторную диаграмму:
- выбираем масштаб:
М: по току: 1см – 7А
по напряжению: 1см – 70В
- откладываем вектора фазных напряжений в масштабе;
- относительно векторов напряжений откладываем вектора фазных токов соответственно нагрузке;
- пользуясь уравнениями, определяем линейные токи:
,
,
Рисунок 15
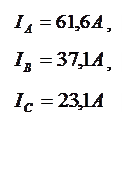
II Символический метод
1.Записываем комплексы полных сопротивлений для каждой фазы:
Ом
Ом
Ом
2.Определим комплексы фазных напряжений:
В
3.Рассчитаем комплексы фазных токов:
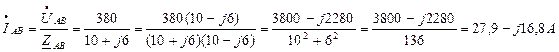
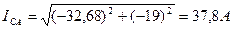
4.Определим комплексы линейных токов:
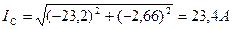
5.Определим мощность в каждой фазе и потребляемую мощность:
|
|
, 
, 
, 
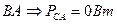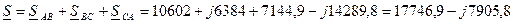
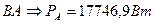
6. Изображаем линейные токи IA, IB, IC; фазные токи IAB, IBC, ICA ; фазные напряжения UAB, UBC, UCA векторами на комплексной плоскости:
Выбираем масштаб:
М: по току: 1 см – 7А
по напряжению: 1 см – 70В
Рисунок 16
Задание 2
Решение данного задания рассмотрим на примере:
Рисунок 17
Решение:
1 Запишем закон изменения напряжения:
2. Определим действующее значение напряжения каждой гармоники в цепи по формулам:
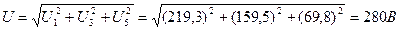
3. Найдем индуктивное, емкостное и реактивное сопротивление для первой гармоники по формулам:
т.к. реактивное сопротивление X1 первой гармоники получилась со знаком «минус» 
в первой гармонике включено емкостное сопротивление
(если X1 получится со знаком «плюс» 
в первой гармонике включено индуктивное сопротивление).
4. Определим полное сопротивление для первой гармоники по формуле:
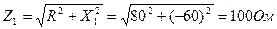
5. Определим максимальное значение тока для первой гармоники по формуле:
6. Определим действующее значение тока для первой гармоники по формуле:
7. Найдем сдвиг фаз между током и напряжением для первой гармоники по формуле:
(значение 
определяем по таблице тригонометрических функций: приложение 6 Евдокимов Ф.Е. «Теоретические основы электротехники»).
8. Определяем емкостное, индуктивное и реактивное сопротивление для третьей гармоники по формулам:
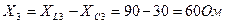
т.к. реактивное сопротивление X3 получилось со знаком «плюс» в третьей гармонике включено индуктивное сопротивление
(если X3 получится со знаком «минус» 
в третьей гармонике включено емкостное сопротивление).
|
|
9. Рассчитаем полное сопротивление третьей гармоники по формуле:
10. Определим максимальное значение тока третьей гармоники по формуле:
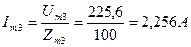
11. Найдем действующее значение тока для третьей гармоники по формуле:
12. Определим сдвиг фаз третьей гармоники по формуле:
13. Определим емкостное, индуктивное и реактивное сопротивление для пятой гармоники по формулам:
т.к. реактивное сопротивление X5 получилось со знаком «плюс» в пятой гармонике включено индуктивное сопротивление
(если X5 получится со знаком «минус» в пятой гармонике включено емкостное сопротивление).
14. Определим полное сопротивление пятой гармоники о формуле:
15. Определим максимальное значение тока пятой гармоники по формуле:
16. Найдем действующее значение тока пятой гармоники по формуле:
17. Определим сдвиг фаз для пятой гармоники по формуле:
18. Запишем закон изменения тока в данной цепи в следующей форме:
(Если реактивное сопротивление тока гармоники имеет емкостный характер, то 
берется со знаком «+»; если индуктивный характер, то 
берется со знаком «-»).
19. Определим действующее значение тока в цепи по формуле:
20. Найдём активную мощность, потребляемую цепью по формулам:
21. Определим коэффициент мощности (cos ) по формуле:
22. Найдём максимальные значения напряжения на ёмкости для каждой гармоники по формулам
23. Запишем закон изменения напряжения на емкости в следующей форме:
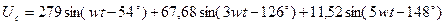
(если реактивное сопротивление тока гармоники имеет емкостный характер, то 
берется со знаком «+»; если индуктивный характер, то 
берется со знаком «-»).
24. Найдем максимальные значения напряжения на индуктивности по формулам:
25. Запишем закон изменения напряжения на индуктивности в следующей форме:
(если реактивное сопротивление тока гармоники имеет емкостный характер, то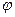 
берется со знаком «+»; если индуктивный характер, то 
берется со знаком «-»)
Задание 3
Решение данной задачи рассмотрим на примере:
Рисунок 18
Решение:
1. Определим активную составляющую тока в цепи по формуле:
2. Определим намагничивающую составляющую тока в цепи по формуле:
3. Найдём ток в неразветвлённой части цепи по формуле:
4. Рассчитаем эквивалентное сопротивление, вызывающее потери в стали по формуле:
5. Определим индуктивное сопротивление по формуле:
6. Начертим схему замещения получившуюся
Схема 1
7. Находим полное сопротивление катушки по формуле:
8. Определим напряжение, подведенное к входным зажимам катушки по формуле:
9. Определим активное и реактивное падение напряжения по формулам:
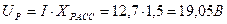
10. Определим угол потерь по формуле:
Значение угла потерь определяем по таблице тригонометрических функций: Приложение 6 Евдокимов Ф.Е. «Теоретические основы электротехники»)
11. Определим потери в стали и потери в меди по формулам:
12. Определим общую мощность потерь в катушке по формуле:
13. Определим коэффициент мощности по формуле:
14. Строим векторную диаграмму в масштабе в следующем порядке:
В произвольном направлении и произвольной длины откладываем вектор магнитного потока фм.. Параллельно ему вектор намагничивающегося тока im (в масштабе) и перпендикулярно вектор активного тока iа (в масштабе). Сумма двух векторов iа и im должна быть равна вектору тока i в обмотке катушки.
Под углом 900 к вектору магнитного потока откладываем вектор напряжения в катушке 
(в масштабе) и в противоположную сторону вектор ЭДС в катушке e=ui .
Параллельно вектору тока i проводим вектор активного падения напряжения ua (в масштабе).
Под углом 900 относительно вектора ua откладываем вектор реактивного падения напряжения UP (в масштабе).
Вектор напряжения U, подводимого к входным зажимам катушки получается путём сложения векторов U’, UA и UP .
Выбираем масштаб:
по току:1 СМ – 2А
по напряжению:1 СМ – 10 В
Рисунок 20
|
