Решение систем дифференциальных уравнений.
 Для решения систем дифференциальных уравнений существует несколько встроенных процедур. Рассмотрим применение процедуры ode45. Как один из возможных форматов вызова, можно предложить такой: [t,r]=ode45(@DiffEquationFunction,[Tstart,Tfinish], StartVector). Отметим, что процедура ode45 может решить систему уравнений следующего вида:
Для решения систем дифференциальных уравнений существует несколько встроенных процедур. Рассмотрим применение процедуры ode45. Как один из возможных форматов вызова, можно предложить такой: [t,r]=ode45(@DiffEquationFunction,[Tstart,Tfinish], StartVector). Отметим, что процедура ode45 может решить систему уравнений следующего вида:  , где
, где  - есть векторная функция
- есть векторная функция  .
.
Рассмотрим пример, иллюстрирующий создание исходной функции DiffEquationFunction для вызова ее процедурой ode45. Пусть некоторая точка массы  движется в гравитационном поле неподвижных точек с массами
движется в гравитационном поле неподвижных точек с массами  и
и  (см. рис.). Уравнение сил в гравитационном поле точек
(см. рис.). Уравнение сил в гравитационном поле точек  и
и  будет следующим:
будет следующим:  . Как видим, данное дифференциальное уравнение имеет второй порядок. Но его можно свести к системе дифференциальных уравнений первого порядка:
. Как видим, данное дифференциальное уравнение имеет второй порядок. Но его можно свести к системе дифференциальных уравнений первого порядка:  .
.
Будем считать, что данная задача является "плоской" и введем следующие обозначения:  ,
,  ,
,  и
и  . Исходя из таких обозначений, систему дифференциальных уравнений движения точки в гравитационном поле можно представить следующим образом:
. Исходя из таких обозначений, систему дифференциальных уравнений движения точки в гравитационном поле можно представить следующим образом:  .
.
Без ущерба для сути решения, значение гравитационной постоянной примем равной 1,  ,
,  ,
,  ,
,  .
.
В таком виде систему уравнений можно уже записать как файл-функцию, что мы и сделали, назвав ее threepoint(t,x).
function f=threepoint(t,x)
M1=50; M2=0; C1x=5; C1y=0; C2x=0; C2y=10;
f = [ x(3)
x(4)
-M1*(x(1)-C1x)/(sqrt((x(1)-C1x)^2+(x(2)-C1y)^2))^3-...
M2*(x(1)-C2x)/(sqrt((x(1)-C2x)^2+(x(2)-C2y)^2))^3
-M1*(x(2)-C1y)/(sqrt((x(1)-C1x)^2+(x(2)-C1y)^2))^3-...
M2*(x(2)-C2y)/(sqrt((x(1)-C2x)^2+(x(2)-C2y)^2))^3 ];
Решим систему дифференциальных уравнений, вызвав процедуру ode45 из файла-функции dynpoint.m.
function dynpoint()
[t,s]=ode45(@threepoint,[0,1000],[0,0,0,4.3]);
x=s(:,1);
y=s(:,2);
x1=5; y1=0; x2=0; y2=10;
plot(x,y,'b-',x1,y1,'r+',x2,y2,'r*');
При таких начальных параметрах ( ) наша точка движется в поле одного объекта.
) наша точка движется в поле одного объекта.
 То, что мы получили вполне можно назвать приемлемым результатом. Нашей целью являлась корректная подготовка системы дифференциальных уравнений для ее решения процедурой ode45. С другой стороны, применяя иные встроенные процедуры можно получить отличающиеся в корне
То, что мы получили вполне можно назвать приемлемым результатом. Нашей целью являлась корректная подготовка системы дифференциальных уравнений для ее решения процедурой ode45. С другой стороны, применяя иные встроенные процедуры можно получить отличающиеся в корне 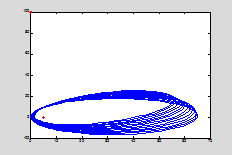 результаты.
результаты.
Попробуем немного поэкспериментировать и введем значение  . Это должно внести возмущения в орбиту движущейся точки.
. Это должно внести возмущения в орбиту движущейся точки.
Крестиком и звездочкой на графике отмечены соответственно  и
и  . Помимо процедуры ode45 существует еще ряд встроенных процедур решения систем дифференциальных уравнений. Их описание можно найти в книгах, указанных в списке литературы. Поскольку, решение систем дифференциальных уравнений является очень важным моментом, то мы не ограничимся одним примером.
. Помимо процедуры ode45 существует еще ряд встроенных процедур решения систем дифференциальных уравнений. Их описание можно найти в книгах, указанных в списке литературы. Поскольку, решение систем дифференциальных уравнений является очень важным моментом, то мы не ограничимся одним примером.
 Рассмотрим следующую задачу, опять же из физики. Рассмотрим траекторию движения пули под действием силы тяжести. При отсутствии сопротивления воздуха, как известно из курса средней школы, это будет парабола. Мы же рассмотрим случай, когда сила сопротивления воздуха пропорциональна квадрату скорости и противоположна направлению движения. Как говорит школьный курс физики, уравнение баланса сил будет следующим:
Рассмотрим следующую задачу, опять же из физики. Рассмотрим траекторию движения пули под действием силы тяжести. При отсутствии сопротивления воздуха, как известно из курса средней школы, это будет парабола. Мы же рассмотрим случай, когда сила сопротивления воздуха пропорциональна квадрату скорости и противоположна направлению движения. Как говорит школьный курс физики, уравнение баланса сил будет следующим:  . Учитывая то, что ускорение – производная скорости по времени, распишем это уравнение в векторном виде:
. Учитывая то, что ускорение – производная скорости по времени, распишем это уравнение в векторном виде:  . Где
. Где  - плотность воздуха,
- плотность воздуха,  - масса пули,
- масса пули,  - площадь поперечного сечения. Распишем это уравнение покоординатно:
- площадь поперечного сечения. Распишем это уравнение покоординатно:  . В таком виде система дифференциальных уравнений готова для того, чтобы попытаться решить ее при помощи процедуры ode45. Пусть масса пули – 10 грамм, поперечник – 1 см2, плотность воздуха – 1 кг/м3. С такими данными мы составим файл-функцию airpoint.m.
. В таком виде система дифференциальных уравнений готова для того, чтобы попытаться решить ее при помощи процедуры ode45. Пусть масса пули – 10 грамм, поперечник – 1 см2, плотность воздуха – 1 кг/м3. С такими данными мы составим файл-функцию airpoint.m.
function u=airpoint(t,v)
g=10; ro=1; s=0.0001; m=0.01; k=ro*s/(2*m);
u = [-k*sqrt(v(1)^2+v(2)^2)*v(1)
-g-k*sqrt(v(1)^2+v(2)^2)*v(2)];
В такой системе уравнений аргументом являются скорость и время. Если мы хотим найти траекторию движения, то мы должны принять во внимание:  . Полученные массивы точек
. Полученные массивы точек  ,
,  ,
,  можно в дальнейшем обработать. Произвести интерполяцию, аппроксимацию и т.д. Но мы интегрирование заменим суммированием:
можно в дальнейшем обработать. Произвести интерполяцию, аппроксимацию и т.д. Но мы интегрирование заменим суммированием:  . В этом случае начальный момент времени равен 0, пуля находится в начале координат. Создадим файл-функцию dynairpoint, в которой вызовем процедуру ode45. В начальный момент времени скорость пули по горизонтали 800, по вертикали – 100.
. В этом случае начальный момент времени равен 0, пуля находится в начале координат. Создадим файл-функцию dynairpoint, в которой вызовем процедуру ode45. В начальный момент времени скорость пули по горизонтали 800, по вертикали – 100.
function dynairpoint()
[t,v]=ode113(@airpoint,[0,5.6],[800,100]);
vx=v(:,1); vy=v(:,2);
m=length(t);
x0=0; y0=0;
% Как улучшить это место до двойной черты?
x(1)=x0; y(1)=y0;
for i=2:m
x(i)=x(i-1)+vx(i-1)*(t(i)-t(i-1));
y(i)=y(i-1)+vy(i-1)*(t(i)-t(i-1));
end;
% ===================================================
[t1,v]=ode113(@airpoint,[0,5.6],[800,100]);
vx1=v(:,1); vy1=v(:,2);
m1=length(t1);
x01=0; y01=0;
% Как улучшить это место до двойной черты?
x1(1)=x01; y1(1)= y01;
for i=2:m1
x1(i)=x1(i-1)+vx1(i-1)*(t1(i)-t1(i-1));
y1(i)=y1(i-1)+vy1(i-1)*(t1(i)-t1(i-1));
end;
% ===================================================
figure
plot(x,y,'r',x1,y1)
grid on
Следует отметить, что диапазон времени [0;5.6] был эмпирическим путем подобран так, что траектория движения отображена от момента вылета до падения. Уровень "земли" соответствует значению ординаты 0. Момент прикосновения к "земле" можно и подсчитать. Оставим это в качестве упражнения. В m-файле dynairpoint.m вызвана не только процедура ode45, но и ode113. Вы можете сравнить результаты.
 Мы решали систему дифференциальных уравнений
Мы решали систему дифференциальных уравнений  . Но можно решить и такую систему уравнений:
. Но можно решить и такую систему уравнений:  . Произведем небольшие изменения и напишем файл-функцию airpoint1.m.
. Произведем небольшие изменения и напишем файл-функцию airpoint1.m.
function u=airpoint1(t,x)
g=10; ro=1; s=0.0001; m=0.01; k=ro*s/2/m;
u = [ x(3)
x(4)
-k*sqrt(x(3)^2+x(4)^2)*x(3)
-g-k*sqrt(x(3)^2+x(4)^2)*x(4)];
Для решения системы четырех дифференциальных уравнений, которая записана файл-функцией airpoint1.m создадим файл-функцию dynairpoint1.m.
function dynairpoin1t()
[t,s]=ode45(@airpoint1,[0,5.6],[0,0,800,100]);
x=s(:,1); y=s(:,2);
[t,s]=ode113(@airpoint1,[0,5.6],[0,0,800,100]);
x1=s(:,1); y1=s(:,2);
figure
plot(x,y,'r-',x1,y1,'b-')
grid on
 В этом случае практически нет различий между решениями ode45 и ode113.
В этом случае практически нет различий между решениями ode45 и ode113.
Упражнения
Решить следующие задачи
1.  Составить и решить уравнение движения бруска на пружине. Массу бруска, коэффициент трения о поверхность и жесткость пружины, считать заданными.
Составить и решить уравнение движения бруска на пружине. Массу бруска, коэффициент трения о поверхность и жесткость пружины, считать заданными.
2. Решить систему уравнений:  .
.
3. Решить систему уравнений:  .
.
4. Решить уравнение:  .
.
5. Решить систему уравнений:  .
.
6. Решить уравнение: 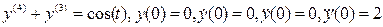 .
.
7. Решить уравнение:  .
.
8. Решить уравнение:  .
.
9. Решить уравнение:  .
.
10. Решить уравнение:  .
.
11. Решить систему уравнений: 
