Методические указания к выполнению лабораторной работы № 3
Тема: Реализация математических моделей линейного программирования для поиска оптимальных решений средствами MS Excel
Цель: изучить методы линейного программирования и способы их реализации в MS Excel
Задание:
1) рассмотреть принцип построения и постановку задачи линейного программирования;
Найти оптимальное решение модели линейного программирования в MS Excel при заданных значениях входных параметров.
Ход работы
Принцип построения и постановка задачи линейного программирования.
1.1. Построение математических моделей линейного программирования.
Математические модели линейного программирования строят на основе известной содержательной постановки задачи.
Составление математической модели начинают с выбора переменных задачи. При этом следует иметь в виду, что в большинстве случаев от удачного выбора этих переменных зависит простота модели а, следовательно, сложность ее решения.
После выбора переменных, исходя из содержательной формулировки задачи, последовательно составляют линейные ограничения, которым эти переменные должны удовлетворять. При этом нужно следить, чтобы в модель были введены все ограничительные условия и в то же время не было ни одного лишнего или записанного в более жесткой форме, чем нужно по условиям задачи.
Следующим шагом является составление целевой функции, которая в математической форме отображает заданный в условиях задачи критерий оптимизации и которая должна быть линейной.
Заметим, что в некоторых моделях удобнее целевую функцию строить сразу после выбора переменных задачи, то есть порядок построения модели не является жестким и может изменяться.
После построения модель, если это возможно, упрощают.
1.2. Постановка задачи линейного программирования.
При составлении суточного рациона откорма скота можно использовать свежее сено (не больше 50 кг) и силос (не больше 85 кг). Рацион должен иметь определенную питательность (число кормовых единиц не менее 30) и содержать питательные вещества: белок (не менее 1 кг), кальций (не менее 100 г) и фосфор (не менее 80 г).
В следующей таблице приведены данные о концентрации необходимых элементов в 1 кг каждого корма и себестоимости (коп./кг) этих кормов.
| Продукты\комп. | Концентрация потребительских элементов в кормах | Себестоимость кормов, коп./кг | |||
| Количество кормовых единиц, кг | Белок, г/кг | Кальций, г/кг | Фосфор, г/кг | ||
| Сено свежее | 0,5 | 1,25 | |||
| Силос | 0,5 | 2,5 |
Необходимо составить оптимальный суточный рацион кормления скота, исходя из условия минимума себестоимости
В таких задачах прежде всего надо определиться, есть ли целевое уравнение. В этой есть - уравнение, которое определяет суточный рацион кормления скота, цель - его минимальная стоимость. То есть фактически нужно уравнение стоимости.
Неизвестными в этом уравнении будут веса составляющих рациона, иксы.
Известны константы при иксах, и известны некоторые ограничения, из которых тоже нужно составить уравнения - уравнения ограничений.
Начнем с них, как с более легких.
Допустим, вес сена свежего Х1 (в таблице MS Excel будет В1 - по адресу). Тогда ограничение для сена - Х1<=50
Аналогично, силос Х2 (В2). Ограничение - Х2<=85
Дальше, известно, что на 1 кг сена и на 1 кг силоса по 0,5 кг кормовых единиц, а в рационе их должно быть не менее 30. То есть больше или ровно. Тогда Х1*0.5+Х2*0.5>=30 (В1*0.5+В2*0.5>=30)
Питательных элементов в сене и силосе:
белок Х1*0.04+Х2*0.01>=1 или В1*0.04+В2*0.01>=1
кальций Х1*0.00125+Х2*0.0025>=0.1 или В1*0.00125+В2*0.0025>=0.1
фосфор Х1*0.002+Х2*0.001>=0.08 или В1*0.002+В2*0.001>=0.08
Теперь уравнение стоимости: Х1*0.03+Х2*0.07→min или В1*0.03+В2*0.07→min
2. Решение задачи проводится с использованием табличного процессорf MS Excel.
Для нахождения иксов необходимо внести все составленные уравнения на лист MS Excel, принимая при этом, что В1-В2 - иксы, то есть пока что пустые ячейки, значение каких MS Excel и будет искать перебором с учетом целевого уравнения и ограничений, в которые эти иксы входят.
Решение модели в MS Excel при заданных значениях входных параметров.
2.1. Введите все уравнения на лист. Уравнение вводим без "меньше или ровно" и "больше или ровно", пределы вводятся позже, в окне поиска решения, в разделе ограничений. На рисунке 1 изображено, как выглядит лист с введенными формулами (подсчитанными и в режиме отображения формул).
 |
2.2. Вызовите пункт меню "Сервис" - подпункт "Поиск решения". Желательно вызывать из ячейки В4 (курсор в ней при загрузке окна поиска), тогда ссылка на целевое уравнение в окне поиска сразу уже будет установлена (см. рис. 2).
Рисунок 1 - Ввод неизвестных, целевого уравнения и уравнений ограничений
 |
Рисунок 2 - Вызов окна "Поиск решения"
2.3. Ввод ограничений в окне "Поиск решения": тех, которые расположены на листе, а также условий не отрицательности.
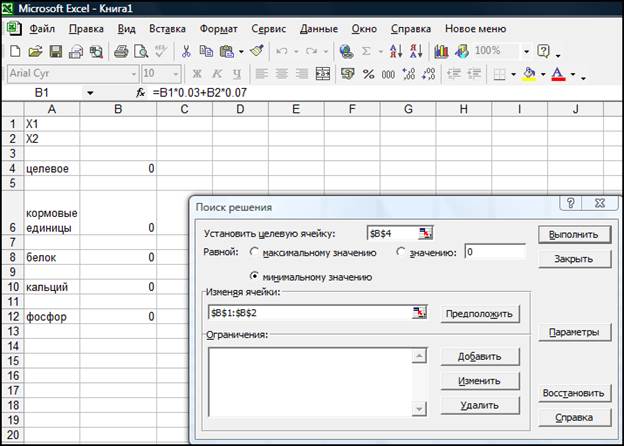
Переключим селектор на "Минимальному значению". Также укажем с помощью кнопки возвращения на лист, какие ячейки нужно изменять табличному процессору MS Excel при поиске решения (перебирать все возможные при ограничениях значения с учетом цели). Это наши иксы В1 и В2 (см. рис. 3).
Добавляйте первое ограничение. Нажмите на кнопку "Добавить", в диалоговом окне, которое появилось, введите ссылку на уравнение кормовых единиц, знак >= выберите из поля со списком, и также введите константу - 0 (см. рис. 4).
 |
Нажмите на кнопку "Добавить".
Рисунок 3 - Вид диалогового окна "Поиск решения" с введенными адресами целевого уравнения и иксов
Снова появится такое же окно для ввода следующего ограничения.
Введите и нажмите "Добавить".
Таким же образом вводим еще 2 ограничения.
Также нужные ограничения просто на сено и силос, без уравнений, сами иксы, которые, во-первых, меньше или уровни соответственно 50 и 85, а также больше или уровни 0 (не отрицательные).
Добавляйте их. В последнем ограничении нажмите "ОК", а не "Добавить".
2.4. Нахождение решения.
Следовательно, в окне "Поиск решения" нажмите на кнопку "Выполнить" (см. рис. 5).
 |
Рисунок 4 - Добавление ограничений в окне "Поиск решения"
Рисунок 5 - Окно "Поиск решения" подготовлено для запуска поиска на выполнение
 |
В результате получено искомое решение - иксы В1 и В2 найдены и заполнены, уравнения в соответствии с ними заполнены посчитанными результатами, можно сохранить найденный результат (см. рис. 6).
 |
Рисунок 6 - Результаты поиска решения
В полученной модели можно изменять коэффициенты и параметры и получать новые варианты суточного рациона кормления.