Определенный интеграл.
Пусть функция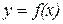 
определена и непрерывна (а значит, ограничена) на [ a,b ].
Разобьем отрезок [ a,b ] на n произвольных частей точками
.
Длину каждого i -го отрезка разбиения назовем
, 
.
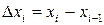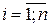Внутри каждого отрезка разбиения выберем произвольно по точке 
.
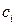Составим сумму
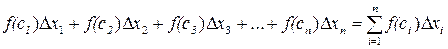. (1)
Выражение вида (1) называется интегральной суммой функции f(x) по отрезку [ a,b ]. Если функция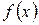 
непрерывна на отрезке 
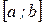, то существует предел интегральной суммы при условии, что длина наибольшего из частичных отрезков стремится к нулю, и он не зависит от способа разбиения отрезка 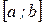на частичные отрезки и от выбора точек 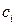в каждом из них.
Опр. Предел интегральной суммы функции f(x) по отрезку [ a,b ] при стремлении длины наибольшего из частичных отрезков к нулю, называется определенным интегралом от функции f(x) по отрезку [ a,b ] и обозначается
.
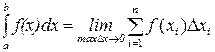Числа а и в называют нижним и верхним пределами интегрирования. Функция называется интегрируемой на отрезке [ a,b ]. Любая непрерывная на отрезке функция интегрируема на этом отрезке.
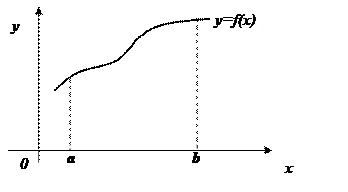
Геометрический смысл определенного интеграла.
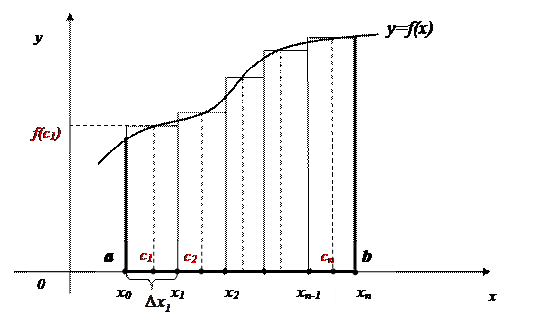
Из рисунка видно, что интегральная сумма равна площади ступенчатой фигуры, образованной из прямоугольников шириной 
, высотой 
. При неограниченном измельчении длин отрезков разбиения площадь этой фигуры стремится к площади криволинейной трапеции. Следовательно, определенный интеграл в геометрическом смысле равен площади криволинейной трапеции, заключенной между графиком неотрицательной функции и осью О х на отрезке [ a,b ].
Свойства определенного интеграла.
1. 
;
2. 
;
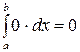3. 
;
4. 
;
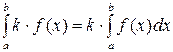5. Пусть функция y=f(x) интегрируема на отрезках [ a,c ] [ b,c ], a<c<b. Тогда она интегрируема и на отрезке [ a,b ], причем
;
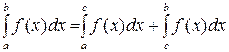6. Если функции f(x) и g(x) интегрируемы по отрезку [ a,b ], то и их сумма также интегрируема по отрезку [ a,b ], причем
.
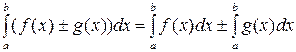7. Если на отрезке [ a,b ] выполняется неравенство 
, то
.
8. Если промежуток интегрирования симметричен, то
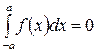, если 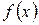- нечетная функция,
и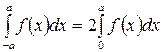 
, если 
- четная функция.
§2. Интеграл с переменным верхним пределом.
Вычисление определенного интеграла.
Пусть функция y=f(x) определена и непрерывна на отрезке [ a,b ]. Тогда она интегрируема как на отрезке [ a,b ], так и на любом меньшем отрезке [ а,х ], где 
[ a,b ]. Значит, величина
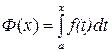
является функцией от х. Она называется интегралом с переменным верхним пределом и является первообразной для функции f(x). Другими словами, функция Ф(х) в каждой своей точке имеет производную, равную f(x):
.
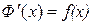Теперь перейдем к вопросу вычисления определенного интеграла.
Теорема. Пусть функция y=f(x) определена и непрерывна на отрезке [ a,b ] и F(х) является первообразной для функции f(x). Тогда
.
(Эта основная формула интегрального исчисления называется формулой Ньютона-Лейбница. Она позволяет сводить вычисление определенного интеграла к нахождению первообразной.)
Док-во. Пусть функция y=f(x) имеет некоторую первообразную F(x). Тогда F(x)=Ф(x)+C, где 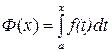- другая первообразная f(x). Имеем:
.▲
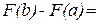
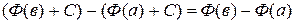
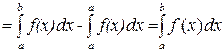Пример.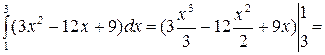 
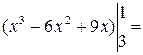
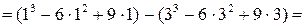1-6+9-27+54-27=4.
Замена переменной в определенном интеграле.
Теорема. Пусть функция y=f(x) непрерывна на отрезке [ a,b ], а функция x=φ(t) определена на отрезке [ α,β ] и имеет непрерывную производную внутри этого отрезка, причем φ(α)=a, φ(β)=b и φ([α,β])=[a,b]. Тогда
.
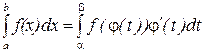Док-во. Пусть F(x) – первообразная для функции f(x), тогда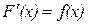 
и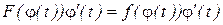 
. Тогда
.▲
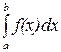Пример. Найти
.
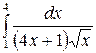Применим подстановку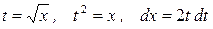 
. Найдем новые пределы интегрирования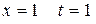: при 
; при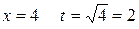 
.
.