Обозначения:
N – множество всех натуральных чисел;
Z – множество всех целых чисел;
Q – множество всех рациональных чисел;
R – множество всех действительных чисел;
R[x] – множество всех многочленов с действительными коэффициентами, аналогично определяются множества Z[x] и Q[x]. Короче эти множества будут называться «кольцами» (см.[10]).
В кольцах имеются, очевидно, три операции: сложение, вычитание, умножение. Многочлен f(x)=a0xn + a1xn-1 +…+ an-1x + an имеет степень n=deg(f), если a0≠0; многочлен, равный нулю, по определению не имеет степени (иногда говорят, что она равна «минус бесконечности»). В Q и R имеется ещё операция деления на ненулевые элементы. С учётом этих замечаний можно отметить, что степень произведения двух многочленов равна сумме степеней сомножителей, степень суммы (разности) не превосходит степеней слагаемых.
Элемент f данного кольца называется обратимым, если существует другой элемент g этого же кольца такой, что f·g=1. Например, для кольца R[x] обратимыми являются многочлены степени 0 (то есть константы, не равные нулю) и только они.
Ненулевой элемент кольца называется неприводимым, если он не представляется в виде произведения необратимых элементов. Для кольца Z неприводимые элементы чаще называются простыми числами.
Многочлен из R[x] или Q[x], не равный нулю, является неприводимым в данном кольце, если он не разлагается в произведение многочленов меньших степеней. Например, многочлен x2 -- 2 неприводим в кольце Q[x] и приводим в кольце R[x], так как x2 – 2=(x --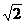 
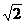)(x + ). Для кольца Z[x] ситуация чуть сложнее.
Аналогично свойствам делимости для целых чисел, для колец R[x] и Q[x] имеется алгоритм деления многочлена на многочлен с остатком «столбиком». Он даёт для любой пары многочленов f и g ≠0 единственную другую пару q и r, такую, что f = g·q + r; при этом deg(r) < deg(g) или r=0. Многочлен f называется делимым, g – делителем, q – (неполным) частным, r – остатком. В случае r=0 говорят, что f делится на g нацело (или без остатка).
Имеются свойства делимости, аналогичные свойствам делимости для кольца Z, при этом роль простых чисел переходит к неприводимым многочленам. Например, справедливо свойство: если произведение f·g делится на неприводимый многочлен h, то один из сомножителей делится на h.
Наибольшим общим делителем двух многочленов f и g называется такой общий делитель d, который делится на любой общий делитель f и g; обозначение: НОД(f, g)=d. Для любой пары ненулевых многочленов НОД существует и определяется однозначно с точностью до обратимого множителя, то есть до константы. Для любых двух ненулевых многочленов f и g существуют два других многочлена u и v, такие, что f·u + g·v = d = НОД(f, g).
Два многочлена f и g называются взаимно простыми, если НОД(f, g)=1. Имеется следующее важное свойство: если НОД(f, g)=1 и многочлен p делится на f и на g, то p делится и на произведение f·g.
Основная теорема арифметики для кольца Z утверждает, что всякое необратимое ненулевое целое число представляется в виде произведения степеней различных простых чисел, и это произведение однозначно с точностью до перестановок сомножителей и до распределения обратимых сомножителей ±1.
Аналогичная теорема для колец R[x] и Q[x] утверждает, что всякий необратимый ненулевой многочлен однозначно разлагается в произведение неприводимых многочленов, с точностью до порядка сомножителей и умножения на обратимые элементы.
Для кольца Z[x] имеется следующее замечание. Для многочлена f(x)=a0xn + a1xn-1 +…+ an-1x + an рассмотрим НОД(a0, a1, …., an-1, an)=c («содержание многочлена f(x)») и вынесем общий множитель: f(x)=c·f1. Теперь у многочлена f1 набор коэффициентов в совокупности взаимно прост. Другими словами, содержание многочлена f1 равно 1. Для таких многочленов справедливо следующее утверждение: если многочлен с содержанием 1 рассмотреть как многочлен из Q[x], то он будет разлагаться на неприводимые в Q[x] так, что все коэффициенты сомножителей можно взять целыми, и все сомножители при этом также будут иметь содержание 1 (см.[10]).
Одним из основных вопросов алгебры многочленов является проблема описания всех неприводимых многочленов. Для кольца R[x] так называемая «основная теорема алгебры многочленов» даёт полную классификацию неприводимых многочленов: это многочлены первого порядка и многочлены второго порядка с отрицательными дискриминантами. Другими словами, всякий многочлен с действительными коэффициентами однозначно разлагается на произведение линейных и квадратичных сомножителей, у которых нет действительных корней. Какого-то алгоритма для нахождения этих сомножителей нет.
Корни многочленов из Z[x] называются алгебраическими числами. Остальные числа называются трансцендентными. Например,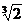 
-- алгебраическое число степени 3, 
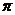-- трансцендентное число. С каждым алгебраическим числом связан неприводимый в Z[x] и в Q[x] многочлен.
Для кольца Q[x] легко можно привести примеры неприводимых многочленов всех положительных степеней. Полное описание неприводимых многочленов затруднительно, однако имеется алгоритм разложения многочлена из Q[x] или из Z[x] на неприводимые. При этом используется метод неопределённых коэффициентов.
Ещё несколько замечаний. Пусть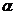 
-- корень многочлена f(x), то есть f(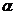)=0. Тогда
f(x)=(x- 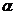)·h(x), то есть f(x)·делится без остатка на x- 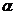. Это теорема Безу.
Если f(x)=a0xn + a1xn-1 +…+ an-1x + an – многочлен с целыми коэффициентами и p/q – рациональный корень многочлена, то p – делитель an, q – делитель a0. Это замечание даёт возможность определения всех рациональных корней многочлена, если они имеются.
Всякий многочлен f(x) имеет не более, чем n=deg(f) корней. В частности, если многочлен степени не выше n равен нулю в n+1 точке, то это – нулевой многочлен.
Для многочленов любой степени справедлива теорема Виета. В частности, для многочленов третьей степени она формулируется так: если числа x1, x2, x3 являются корнями многочлена ax3 +bx2 +cx + d, то x1 + x2 + x3 =--b/a, x1x2 + x2x3 + x1x3 = c/a, x1x2x3 = -- d/a.
Задачи.
Если в задаче не указано, что требуется сделать, подразумевается, что надо доказать утверждения, сформулированные в задаче, и/или ответить на соответствующие вопросы.
1. Разложение на множители в Z[x]:
x5 +x +1, x8 + x + 1, x8 + x7 + 1, x8 + 3x4 + 4 -- на два множителя, x8 + x4 + 1— на три множителя, x9 + x4 – x -- 1 – на пять множителей, – [1, 4]
2. (x+1)2n – x2n – 2x -- 1 делится на x(x+1)(2x+1);
3. При каких a и b многочлен xn – axn-1 + bx -- 1 делится на (x--1)2?
4. Существует ли многочлен p(x) с целыми коэффициентами такой, что a) -- p(0)=19, p(1)=85, p(2)=1985? b) -- p(1)=19, p(19)=85?
5. f(x) при делении на x--1 даёт остаток 3, при делении на x—2 – остаток 5. Какой остаток даст этот многочлен при делении на (x--1)(x--2)?
6. f(x) при делении на x--1 даёт остаток 2, при делении на x—2 – остаток 1. Какой остаток даст этот многочлен при делении на (x--1)(x--2)?
7.
8. f(x)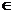 
Z[x] и |f(3)| = |f(7)| =1. Тогда этот многочлен не имеет целых корней.
9. Пусть многочлен f(x) 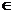Z[x] и f(a) -- f(b) =1 для некоторых целых a и b. Доказать, что тогда
|a – b| = 1.
10. f(x) 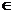Z[x] и f(0) и f(1) нечётны. Тогда этот многочлен не имеет целых корней.
11. Пусть f(x) 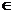Z[x], степени 7. Если его значения при пяти различных целых значениях x по модулю равны 1, то многочлен не разлагается в произведение многочленов ненулевой степени с целыми коэффициентами.
12. Пусть f(x) 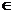Z[x] и при четырёх целых значениях x f(x) = 7; тогда f(x)≠14 ни при каких целых x.
13. Многочлен x5–2 неприводим в Q[x], то есть не разлагается в произведение многочленов меньших степеней с рациональными коэффициентами.
14. Многочлен x250 + x249 + … +x2 + x + 1 не разлагается в произведение многочленов с целыми коэффициентами.
15. 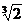не удовлетворяет никакому квадратному многочлену с целыми коэффициентами.
16. Построить многочлен с целыми коэффициентами, корнем которого было бы число + .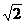
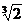17. Сумма, произведение, частное алгебраических чисел – также является алгебраическим числом; (определения приведены ранее).
18. При каких a многочлены x4 + ax2 + 1 и x3 + ax + 1 имеют общий корень?
19. Доказать, что многочлен x95 + x94 + … +x2 + x + 1 делится на многочлен x31 + x30 + … +x2 + x + 1 – [4].
20. Доказать, что многочлен x9999 + x8888 + … +x2222 + x1111 + 1 делится на многочлен x9 + x8 + … +x2 + x + 1 – [8].
21. Решить уравнение (x--1)(x--3)(x+5)(x+7)=297.
22. Решить уравнение (x--4)(x--5)(x -- 6)(x -- 7)=1680.
23. Решить уравнение (x+2)4 + x4 =82 – [4].
24. Найти все положительные решения уравнения x1985 + 19861986 = x1986 + 19861985. – [11].
25. Найти остаток от деления многочлена x243 + x81 +x27 + x9 +x3 + x на x—1, на x2 – 1.
26. Найти сумму коэффициентов многочлена (1—3x+3x2)743 (1+3x--3x2)744.
27. Найти коэффициент при x50 в многочлене а) -- (1+x)1000 + x(1+x)999 + x2(1+x)998 + … + x1000, в многочлене б) -- (1+x) + 2(1+x)2 + 3(1+x)3 + … + 1000(1 + x)1000.
28. Доказать, что в многочлене (x100-- x99 + … +x2 -- x + 1)(x100 + x99 + … +x2 + x + 1) после приведения его к стандартному виду все коэффициенты при нечётных степенях будут равны 0.
29. Если многочлен является чётной функцией, то все коэффициенты при нечётных степенях x равны 0, если нечётной – все коэффициенты при чётных степенях равны 0.
30. В каком многочлене коэффициент при x20 больше: в (1 + x2 – x3)1000 или в (1 -- x2 + x3)1000?
31. При любом x справедливо неравенство:
(x100 + x98 + … +x4 + x2 + 1)(1 + x102) – 102x 101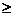 
0.
32. При делении многочлена x1951 – 1 на x4 + x3 + 2x2 + x +1 получаются частное и остаток. Найти в частном коэффициент при x14.
33. Найти количество нечётных коэффициентов многочлена (1 + x + x2)1992.
34. Найти все многочлены p(x), для которых справедливо тождество: x·p(x--1)=(x--26)·p(x).
35. Пусть квадратный трёхчлен f(x) не имеет корней. Тогда и уравнение f(f(x)) = x не имеет корней.
36. При каких а уравнения 1 + ax + x2 =0 и a + x + x2 = 0 имеют общий корень?
37. Найти целое число a такое, что (x -- a)(x -- 10) + 1 разлагается в произведение (x + b)(x + c) двух множителей с целыми b и c.
38. Найти такие ненулевые различные целые числа a, b, c, что многочлен x(x -- a)(x – b)(x -- c) + 1 разлагается в произведение многочленов с целыми коэффициентами.
39. Доказать, что при любых отличных друг от друга целых числах a1, a2, … an многочлен
(x -- a1)2(x – a2)2·… (x – an)2+1 не разлагается в произведение многочленов с целыми коэффициентами.
40. Найти все решения уравнения x3 + (x+1)3 + (x+2)3 = (x+3)3 в целых числах.
41. Найти все решения уравнения x3 + (x+1)3 + (x+2)3 + (x+3)3= (x+4)3 в целых числах.
42. Найти все решения уравнения x3 + (x+1)3 + (x+2)3 + (x+3)3= (x+9)3 в рациональных числах.
43. Пусть f(x), g(x), h(x) – три квадратных трёхчлена с положительными старшими коэффициентами. Известно, что каждый из них имеет хотя бы один общий корень с суммой двух других. Доказать, что тогда f(x), g(x), h(x) имеют общий корень.
44. Многочлен f(x) 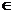Z[x] при x=0 и при x=1 принимает нечётные значения. Тогда многочлен не имеет целых корней.
45. Если многочлен степени n принимает целые значения при x=0, 1, 2, … n, то этот многочлен принимает целые значения при всех целых x. Такие многочлены называются целозначными.
46. Привести пример целозначного многочлена с дробными коэффициентами.
47. Если многочлен f(x) 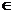Q[x] степени n принимает целые значения при x=0, 1, 4, 9, … n2, то он принимает целые значения и при любых квадратах целых чисел, но не обязан быть целозначным. – [2].
48. Не существует такого многочлена f(x),что все значения f(0), f(1), f(2), … являются простыми числами.
49. Даны три квадратных трёхчлена: f1(x) = x2 + p1x + q1, f2(x) = x2 + p2x + q2, f3(x) = x2 + p3x + q3. Доказать, что уравнение |f1(x)| + |f1(x)| = |f1(x)| имеет не более восьми корней. – [7]
50. Известно, что a + b +c =5, ab + ac + bc =5. Чему может быть равно выражение a2 + b2 +c2? – [9]
51. Пусть многочлен f(x, y) с действительными коэффициентами равен нулю на всех точках стандартной окружности x2 + y2 = 1. Тогда существует такой многочлен g(x, y), что f(x, y) = (x2 + y2 -- 1) g(x, y).
52. Многочлены p(x) и q(x) таковы, что p(x3) + q(x3) делится на x2 + x + 1. Тогда p(x) и q(x) делятся на x –1.
53. Уравнение x6 – 6x5 + 15x4 + ax3 + bx2 + cx + d = 0 имеет шесть корней. Определить коэффициенты a, b, c, d. – [8]
54. Привести пример многочлена третьей степени с целыми коэффициентами, имеющего три различных иррациональных корня.
Литература
1. Н.Б. Васильев, В.Л. Гутенмахер, Ж.М. Раббот, А.Л. Тоом Заочные математические олимпиады М., Наука, 1986
2. Д.Щ. Шклярский, Н.Н. Ченцов, И.М. Яглом Избранные задачи и теоремы элементарной математики – арифметика и алгебра М., Наука, 1976
3. И. С. Петраков Математические олимпиады школьников М., Просвещение, 1982
4. И.Л. Бабинская Задачи математических олимпиад М., Наука, 1975
5. Г.И. Зубелевич Сборник задач московских математических олимпиад М., Просвещение, 1967
6. Г. Штейнгауз Сто задач М., Физ -мат- лит 1959
7. С.Л. Берлов, К.П. Кохась, Д.В. Фомин Задачи математических олимпиад СПб, 1994
8. Задачи отборочных математических олимпиад М., 1992
9. И.О. Бугаенко Турниры им. Ломоносова М., 1993
10. Б. Л. Ван дер Варден Алгебра М., Наука, 1976
11. Фомин Д.В. Задачи ленинградских математических олимпиад Ленинград, 1990