РАЗБИЕНИЯ МНОЖЕСТВ НА ЧАСТИ

Пусть задано множество S = { a ₁,..., a_n }. Требуется распределить элементы S по k именованным множествам S ₁,..., S _k так чтобы в S ₁ попало n ₁ элементов, в S ₂ - n ₂ элементов,..., в S _k - n _k элементов множества S. При этом всякий элемент множества S попадает лишь в одно из множеств S ₁,..., S _k.

Поэтому справедливы соотношения:

S = S_i и n = | S_i |.

Такое распределение элементов S среди множеств S ₁,..., S_k называется разбиением S на части, имеющие заданные мощности. При этом множества, на которые разбивается S, являются именованными, то есть различаются не только по составу, но и по именам. Поэтому в задаче разбиения S на части важно не только выделение систем подмножеств с заданными мощностями, на которые распадается исходное множество, но и то какие множества образуют какие части.

Рассмотрим несколько примеров задач, приводящих к разбиениям множеств на части.

1. Имеется 15 разных картин, которые требуется разместить в трех залах музея так, чтобы в первом зале было выставлено 6 картин, во втором - 5 картин, в третьем - 4 картины.

Всякое распределение картин по залам, с выполнением сформулированных условий, является разбиением множества из 15 картин на три части, мощности которых равны соответственно 6, 5, 4.

2. Требуется распределить 20 заданий поровну между пятью служащими.

Любое распределение заданий представляет собой разбиение множества всех заданий на 5 подмножеств, каждое из которых содержит четыре элемента.

Выведем формулу для нахождения числа различных разбиений конечного множества на части.

Пусть задано множество S = { a ₁,..., a _n }, которое требуется разбить на k подмножеств S ₁,..., S_k, содержащих соответственно по n ₁,..., n _k элементов.

Возьмем произвольную перестановку a _{i 1},..., a _in элементов S. Для этой перестановки определим разбиение S на части, полагая, что первые n ₁ элементов в ней образуют множество S ₁, следующие за ними n ₂ элементов перестановки образуют S₂ и т.д. Последние n_k элементов перестановки образуют множество S_k. Приведённое правило определяет отображение множества перестановок элементов S во множество разбиений S на части.

Определим свойства этого отображения.

Пусть множества S ₁,..., S_k образуют разбиение S на части с заданными количествами элементов в них. Тогда всякое размещение без повторений всех элементов S, получаемое выписыванием без повторений сначала всех элементов S ₁, затем всех элементов S ₂ и т.д., пока не будут выписаны без повторений все элементы множества S_k, образует перестановку элементов S. Такая перестановка отображается в исходное разбиение S ₁,..., S_k. Поэтому отображение перестановок множества S в разбиения S является сюрьективным.

Число перестановок, порождающих одно и то же разбиение множества S на части равно количеству последовательностей, составленных из перестановок элементов множеств S ₁,..., S_k, то есть определяется выражением: n ₁!... n _k!.

Поскольку всего существует n! перестановок элементов A, и каждому разбиению S соответствует n ₁!... n _k! таких перестановок то число различных разбиений S на части S ₁,..., S_k равно

.

Применение последней формулы к приведенному ранее примеру задачи на распределение картин по трем залам музея позволяет утверждать, что существует ровно 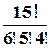вариантов такого распределения.

Упражнения

1. Покажите, используя только комбинаторные доводы (т.е. не прибегая к арифметическим преобразованиям), что число разбиений множества мощности n, на именованные подмножества, имеющие мощности n ₁,..., n_k, равно:

... .

2. Сколько существует разбиений множества S = { a ₁,..., a _n } на части S ₁,..., S_k, имеющие произвольные, в том числе равные нулю, мощности.

3. Сколько имеется способов разбиения n -элементного множества на неименованные части, содержащие n ₁,..., n _k элементов.

Введенные в рассмотрение комбинаторные конструкции размещений, перестановок, сочетаний и разбиений позволяют решать несложные комбинаторные задачи на представление структуры комбинаторных объектов, составляющих заданные множества, а также определять число элементов в этих множествах.

Процесс решения таких задач состоит в том, чтобы представить элементы множеств в виде конструкций, составленных с помощью размещений, сочетаний или разбиений. При построении таких конструкций может потребоваться использование правил сложения и умножения. Для этого строится подходящее разбиение исходного множества на более однородные классы элементов. При необходимости некоторые классы могут быть дополнительно разбиты на подклассы. Процесс разбиения на подклассы продолжается до получения классов, элементы которых могут быть подсчитаны с помощью уже известных комбинаторных конструкций и соотношений для них. Для множеств, элементы которых значительно различаются между собой по структуре, возможна ситуация, когда разбиение на классы приводит к системе одноэлементных или близких к ним множеств.

В качестве примера рассмотрим следующую задачу.

Сколькими способами можно распределить 10 различных предметов среди трех человек, которых обозначим как a, b и c, так чтобы каждому досталось не менее двух предметов.

Понятно, что формула числа разбиений на части для решения этой задачи непосредственно не применима, поскольку мощности множеств предметов, назначаемых a, b и c, на которые разбиваются 10 предметов, не имеют фиксированные мощности и могут изменяться.

Кажется правдоподобным, что решение рассматриваемой задачи можно получить через рассмотрение таких распределений предметов, при котором сначала a, b и c получают по два предмета, а после этого между ними произвольным образом распределяются оставшиеся 4 предмета. Число вариантов выполнения первого действия равно . Количество способов выполнения второго действия, для каждого способа выполнения первого действия представляется четырёхэлементным размещением с повторениями из элементов множества { a, b, c }. В этом размещении на первом, втором, третьем, четвертом месте указан человек, который получает соответственно первый, второй, третий и четвёртый предмет из, числа предметов нераспределенных после первого действия. Следовательно, второе действие можно выполнить = 4 ³ разными способами. Тогда предполагаемый ответ представляет собой произведение чисел и 4 ³.

Однако нетрудно убедиться в том, что если один человек получает 4 предмета, а два других человека - по 3 предмета, то одни и те же предметы могут назначаться первому человеку несколькими разными способами при выполнении приведенной выше последовательности из первого и второго действия.

Поэтому разные способы выполнения указанного распределения предметов приводят к одному и тому же распределению предметов между a, b и c. Как следствие, число таких распределений не равно числу последовательностей из двух действий, определяемых по правилу умножения как произведение числа вариантов выполнения первого шага на число вариантов выполнения второго шага.

Будем решать рассматриваемую задачу через разложение множества всех распределений предметов среди трёх человек на непересекающиеся случаи, каждый из которых определяется своим набором значений числа предметов, достающихся a, b и c.

Для этого построим все различные разбиения числа 10 на три слагаемых, каждое из которых не меньше, чем 2. Число 10 не велико. Поэтому все варианты можно перебрать, выписывая тройки чисел, суммы которых равны 10, в порядке убывания значений элементов в них. Тогда множество всех наборов из трех чисел, суммы которых равны 10, для которых не уточняются количества предметов каждого конкретного человека, имеет вид:

{(6, 2, 2), (5, 3, 2), (4, 4, 2), (4, 3, 3)}.

Рассмотрим последовательно все 4 случая.

1. Для набора (6, 2, 2) имеется ровно способов назначения чисел набора в качестве числа предметов, получаемых a, b и c. (Это следует из того, что достаточно выбрать одного из 3 лиц, который получит 6 предметов.)

После этого для каждого способа такого назначения чисел 6, 2 и 2 между a, b и c существует ровно способов разбиения множества предметов на 3 именованных подмножества, содержащих соответственно 6, 2 и 2 элементов.

По правилу умножения число вариантов распределения предметов в рассматриваемом случае равно: .

2. Для набора (5, 3, 2) существует способов назначения чисел этого набора в качестве количеств предметов, получаемых a, b и c.

Для каждого способа такого назначения существует способов разделения множества предметов между тремя лицами.

Поэтому число вариантов разбиения множества предметов во втором случае равно .

3. Для набора (4, 4, 2) окончательное число вариантов равно:

.

4. Для набора (4, 3, 3) окончательное число вариантов равно:

.

На основании правила сложения, суммируя число вариантов в каждом из перечисленных случаев, получим, что искомое число распределений предметов равно:

+ + + .