Существуют три правила, называемые основными комбинаторными правилами, на основе которых могут быть выведены другие специальные комбинаторные соотношения. Они связаны с подсчетом числа комбинаторных объектов, допускающих структурное представление в виде последовательностей или множеств, обладающих простыми свойствами.
1. Правило птичьих гнезд
Если имеются n + 1 птицы, которых необходимо разместить в n гнездах, то при любом способе размещения хотя бы в одном гнезде окажется не менее двух птиц.
Для обоснования справедливости приведенного правила воспользуемся методом рассуждений от противного. Предположим, что данное правило неверно. Пусть после распределения птиц в каждом гнезде оказалось не более чем по одной птице. Перенумеруем гнёзда, в которые попало по птице натуральными числами 1,..., k. Поскольку в гнёзда попало всего k птиц и k £ n, то в гнёздах оказались размещены не все птицы. Из получаемого противоречия следует, что предположение о противном неверно, а, значит, верно правило птичьих гнёзд.
2. Правило умножения.
Пусть необходимо строить все возможные n -элементные последовательности a 1,..., a n, для которых выполнены условия:
a) первый элемент таких последовательностей может быть выбран m 1 способами;
b) если i < n, то для каждого способа выбора значений первых i элементов последовательности значение i+ 1-го элемента таких последовательностей может быть выбрано mi+ 1 способами.
Тогда число различных последовательностей a 1,..., a n равно:
m 1 m 2 ... m n.
Обосновать справедливость правила умножения можно, например, математической индукцией по значению n.
Базис индукции
Для n = 1 правило умножения является справедливым, так как существует ровно m 1одноэлементных последовательностей, первый элемент которых можно выбрать m 1 разными способами.
Индуктивное предположение
Пусть для n = k количество различных последовательностей, удовлетворяющих условиям правила умножения, равно m 1 m 2... mk.
Индуктивный переход
Пусть n = k + 1. По индуктивному предположению существует ровно m 1 m 2... mk различных последовательностей длины k, удовлетворяющих условиям правила умножения, каждая из которых при добавлении еще одного элемента преобразуется в mk+ 1 различных последовательностей длины k + 1, также удовлетворяющих условиям этого правила. Поэтому общее число последовательностей длины k + 1 в mk +1 раз больше числа различных последовательностей, имеющих длину k. То есть всего таких последовательностей ровно m 1 m 2... mk mk +1.
3. Правило сложения
Пусть заданы непересекающиеся конечные множества A 1 ,..., Ak. Тогда мощность объединения этих множеств может быть определена по формуле:
| 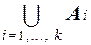 | =
| =  .
.
Для обоснования справедливости правила сложения заметим, что в значении левой части записи правила каждый элемент объединения непересекающихся множеств A 1 ,..., Ak учтен ровно один раз. Значение в правой части правила учитывает все элементы каждого из множеств A 1 ,..., Ak. Поскольку последние множества непересекающиеся, то всякий элемент их объединения учитывается в правом значении также ровно один раз. Это означает справедливость правила сложения.
Правило умножения - основное для определения количества комбинаторных объектов. К нему сводятся различные вспомогательные комбинаторные соотношения и задачи, преобразуемые в семейства задач, решаемых с помощью этого правила.
Рассмотрим примеры задач, в которых применимо или неприменимо правило умножения.
Пример 1. Определить число различных двоичных наборов длины n, содержащих нечетное число единиц.
Решение
Очевидно, что если n > 1, то первая цифра таких наборов может быть выбрана двумя разными способами. Для всякого i < n - 1 и выбранного начала набора длины i значение следующей цифры набора может быть выбрано двумя способами. Если уже выбраны значения первых n – 1 цифр набора, то значение последней цифры может быть выполнено единственным способом так, чтобы дополнить сумму предшествующих цифр до нечетного значения. Поэтому условия правила умножения выполнены со значениями m 1,..., m n-1, m n, равными 2,..., 2, 1. Следовательно, число двоичных наборов, содержащих нечетное число единиц, равно 2 n-1.
Пример 2. Сколько различных последовательностей десятичных цифр длины 12 можно составить так, чтобы каждая последующая цифра последовательности была не меньше предыдущей.
Решение
Понятно, что первая цифра в таких последовательностях может быть выбрана любой, а число выборов значения каждой последующей цифры в последовательности зависит от предшествующей ей цифры набора. Например, двухэлементная последовательность 2, 3 может быть продолжена 8 способами, а другую двухэлементную последовательность 2, 5 можно продолжить лишь 6 разными способами. Следовательно, для данной задачи условия правила умножения не выполнены. Поэтому для её решения, нельзя использовать правило умножения.
Правило сложения обычно применяется в случаях, когда множество комбинаторных объектов неоднородно, не может быть представлено конструкциями одной и той же структуры, для которой существует простая формула определения числа разных конструкций.
В таких случаях множество всех объектов разбивается на конечное число непересекающихся и более простых классов, в каждом их которых задача подсчета количества объектов может быть решена. Тогда число элементов исходного множества равно сумме мощностей всех непересекающихся классов, на которые было разбито исходное множество.
Рассмотрим пример задачи, решаемой с помощью правила сложения.
Пусть требуется определить число различных слов в английском алфавите, имеющих длину 7 и начинающихся либо с символов WH, либо с символа F. Напомним, что английский алфавит состоит из 26 символов.
Очевидно, что заданное множество слов распадается на две части:
1) множество A 1 - слова, начинающиеся с WH;
2) множество A 2 - слова, начинающиеся с F.
С помощью правила умножения можно показать, что A 1 содержит 265 различных слов, а A 2 - 266 слов. Поэтому общее количество слов в рассматриваемом множестве равно
265 + 266 = 265 · 27.
РАЗМЕЩЕНИЯ И СОЧЕТАНИЯ
Пусть D - конечное множество, содержащее n элементов.
ОПРЕДЕЛЕНИЕ
Размещениями из n элементов по m элементов множества D называются m -элементные последовательности, каждый член которых является элементом D.
Здесь предполагается, что m ³ 0. При этом, если m = 0, то соответствующее размещение не содержит ни одного элемента и является пустым.
Если множество D неизвестно или не уточняется, то говорят о размещениях из n по m.
Например, слово FALKON может рассматриваться как размещение из 26 элементов символов английского алфавита по 6.
Размещение называется размещением без повторений, если все входящие в него элементы являются разными.
Заметим, что для размещений с повторениями должно выполняться условие m 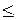 n, так как в противном случае по правилу птичьих гнезд в размещении, длина которого больше числа элементов множества, из которого выбираются элементы размещения, будет повторяться хотя бы один символ.
n, так как в противном случае по правилу птичьих гнезд в размещении, длина которого больше числа элементов множества, из которого выбираются элементы размещения, будет повторяться хотя бы один символ.
Размещение, в котором могут встречаться одинаковые элементы, называется размещением с повторениями. Из приведенных определений следует, что всякое размещение без повторений одновременно является и размещением с повторениями.
Размещения используются для представления таких комбинаторных объектов, каждому элементу которых должно быть сопоставлено свойство, отличающее его любого из остальных элементов в составе объекта.
Определим число различных размещений из n по m без повторений. В таких размещениях первый элемент может быть выбран n способами, при всяком способе выбора первого элемента выбор второго элемента может быть осуществлен n - 1 разными способами и т.д. При всяком способе выбора значений первых m - 1 элементов последний m -й элемент может быть выбран n - m + 1 способом.
По правилу умножения число таких размещений не зависит от множества A и равно значению произведения:
n × (n - 1) ×... × (n - m + 1).
Для обозначения число размещений без повторений из n по m применяется специальное выражение 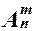 . Поэтому:
. Поэтому: 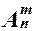 =
= 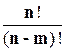 .
.
В размещениях из n по m с повторениями каждый элемент такого размещения может быть выбран n способами. Поэтому по правилу умножения число размещений с повторениями из n по m равно  .
.
Число размещений с повторениями обозначается как 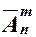 . Следовательно, справедливо соотношение:
. Следовательно, справедливо соотношение: 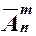 =
=  .
.
Частным случаем размещений без повторений являются размещения всех элементов множества или перестановки элементов множества. Как следует из приведенных формул число Pn перестановок элементов произвольного n элементного множества равно n!
ОПРЕДЕЛЕНИЕ
Сочетанием из n элементов по m элементов n-элементного множества D называется всякая совокупность, состоящая из m элементов D.
Если множество D неизвестно или не уточняется, то говорят о размещениях из n по m.
Так же, как и для размещений, предполагается, что m ³ 0. Если m = 0, то такое сочетание не содержит элементов, т.е. является пустым множеством.
Как следует из приведенного определения в сочетаниях, в отличие от размещений, важен только состав входящих в них элементов, которые в составе сочетания не различаются между собой.
Сочетания могут быть с повторениями и без них.
В сочетании без повторений все элементы совокупности являются разными. Для существования таких сочетаний необходимо выполнение дополнительного условия n ³ m. Всякое такое сочетание может рассматриваться как подмножество того множества, из которого выбираются элементы сочетания. Поэтому множества всех сочетаний без повторений некоторого конечного множества и множество подмножеств этого множества равны.
Из приведенных определений следует, что в сочетании с повторениями могут содержаться одинаковые элементы. Поэтому сочетания без повторений одновременно являются и сочетаниями с повторениями.