Тема 1. Множества и операции над ними
Понятие множества и элемента множества
В математике часто рассматриваются те или иные группы объектов как единое целое: натуральные числа, треугольники, квадраты и т.д. Все эти различные совокупности называют множествами.
В обыденной речи слово «множество» используется для обозначения большого количества предметов. В математике можно рассматривать множество, состоящее из одного объекта, и множество, не содержащее ни одного объекта.
Множества принято обозначать прописными буквами латинского алфавита: A, B, C, …, Z.
Множество, не содержащее ни одного объекта, называют пустым множеством и обозначают 
.
Объекты, из которых образовано множество, называют элементами.
Элементы обозначают строчными буквами латинского алфавита: а,б,в
Множества бывают конечные и бесконечные. Конечными являются множества дней недели, месяцев в году, дней в году, бесконечными – множество точек на прямой, множество натуральных чисел и т.д.
Для ряда числовых множеств в математике приняты стандартные обозначения:
Числовые множества:
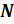– множество натуральных чисел;
– множество целых неотрицательных чисел (
= 
+ нуль);
– множество целых чисел (
= + целые отрицательные числа);
– множество рациональных чисел (
= + дробные числа);
– множество действительных чисел (
= + иррациональные числа).
Способы задания множеств
Множество определяется своими элементами.
Говорят, что множество задано, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит.
В математике часто приходится выяснять, принадлежит объект какому-либо множеству или не принадлежит.
Предложение «Объект 
принадлежит множеству А» можно записать, используя символы 
.
Предложение «Объект не принадлежит множеству А» можно записать, используя символы 
.
а) Пусть A – множество однозначных чисел.
Утверждение «Число 3 – однозначное» можно записать как
. Запись 
означает, что «Число 12 не является однозначным числом», или «Число 12 не принадлежит множеству 
», или «Множество не содержит числа 12».
Множество можно задать следующими способами:
1. Перечислением всех его элементов.
2. Указанием характеристического свойства.
Характеристическое свойство множества – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
б).Запись А={х / х>2 } означает, что множество А состоит из всех таких чисел, которые больше 2, или говорят, что множество А задано описанием характеристического свойства.
1.3 Отношения между множествами и их изображение с помощью кругов Эйлера:
1. Пересечением множеств A и B называют множество, содержащее те и только те элементы, которые принадлежат множеству A и множеству B.
Пересечение множества А и В обозначают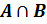 
.
| A |
| В AÇB |
В случае, когда множества А и В не имеют общих элементов, говорят, что их пересечение пусто, и пишут 
.
Множество B называют подмножеством множества A,
если каждый элемент множества B является также элементом множества А.
Записывают: 
.
Пустое множество считают подмножеством любого множества.
Любое множество является подмножеством самого себя.
С).Дано множество, состоящее из трёх элементов а,б,с. Найти все его подмножества.
2.Множества A и B называют равными, если 
и .
| A=B |
Записывают: A=B.
Равные множества состоят из одних и тех же элементов, и порядок записи элементов множества не существен.