Вращение прямой линии вокруг проецирующей прямой

Вращение точки вокруг проецирующей прямой

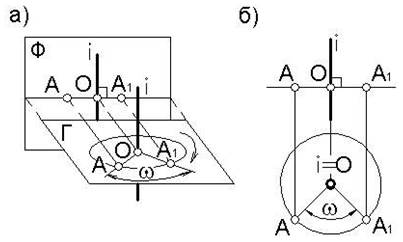Рассмотрим вращение точки А вокруг горизонтально проецирующей прямой i (рисунок 78). Плоскость, в которой точка описывает окружность, будет горизонтальной плоскостью уровня, поскольку перпендикулярна к горизонтально проецирующей прямой i. Окружность, которую описывает точка А при вращении, проецируется на виде сверху (на горизонтальной проекции) без искажения, а на виде спереди (на фронтальной проекции) – в виде прямой линии перпендикулярной линиям связи.

Рисунок 78

Выполним для примера поворот точки А вокруг оси i на некоторый угол ω по направлению движения часовой стрелки. Для этого на виде сверху (на горизонтальной проекции) проведем окружность с центром в точке О и радиусом АО. В нужном направлении откладываем угол ω =АОА1, получая при этом горизонтальную проекцию нового положения точки А – А1. Фронтальная проекция нового положения точки А определяется на проекции плоскости, в которой происходит вращение точки А.

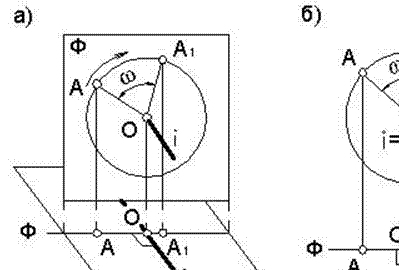
Если точка вращается вокруг фронтально проецирующей прямой i, то плоскость окружности вращения будет фронтальной плоскостью уровня (рисунок 79). На виде спереди (фронтальной проекции) эта окружность проецируется без искажения, а на виде сверху (горизонтальной проекции) – в виде отрезка прямой, перпендикулярной линиям связи.

Таким образом, при вращении точки вокруг проецирующей прямой одна проекция точки (та, где прямая “вырождается” в точку) перемещается по окружности, а другая – по прямой перпендикулярной линиям связи.

 

Вращение прямой линии вокруг проецирующей прямой

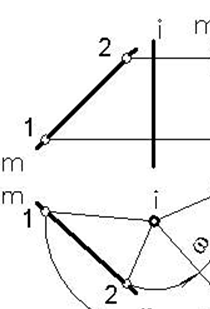Так как прямая определяется двумя точками, то вращение прямой сводится к вращению этих двух точек.

Рассмотрим пример поворота прямой общего положения т на угол ω против движения часовой стрелки (рисунок 80).

Выбрав на прямой две произвольные точки 1 и 2, повернем каждую из них в заданном направлении на заданный угол ω. Новые положения точек 11 и 21 определят новое положение прямой т после поворота – т 1.

Здесь равны треугольники Δ1-2- I = Δ11-21- i, по двум равным сторонам 1- I = 11- i и 2- I = 21- i и равным углам ω между ними. Принимая во внимание, что отрезки 1-2 и 11-21 равны (как стороны равных треугольников) можно сделать вывод: расстояние между проекциями точек прямой линии при ее повороте на некоторый угол вокруг проецирующей прямой остается неизменным на той проекции, где траектория вращения проецируется без искажения – в виде окружности.

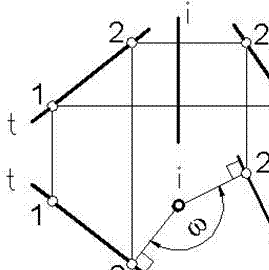Это свойство позволяет несколько упростить построение новых проекций прямой при повороте вокруг проецирующих прямых. На рисунке 81 выполнен поворот прямой t вокруг горизонтально проецирующей прямой i с применением упрощенных построений. Как и ранее, прямая задана двумя точками 1 и 2. Но если точка 1 выбрана произвольно, то точка 2 определяется на перпендикуляре, опущенном из точки i (в которую проецируется прямая i) на прямую t.

Рисунок 81

Ход построений следующий: точка 2 повернута на заданный угол ω вокруг прямой i. Затем через новое положение точки 21 на виде сверху (на горизонтальной проекции) перпендикулярно отрезку i -21 проводим новое положение прямой t. Поскольку отрезок 1-2 при вращении не меняет своей длины, то откладывая от точки 21 его длину до поворота, получаем новое положение горизонтальной проекции прямой t. Вид спереди (фронтальная проекция) нового положения прямой t после поворота находится после определения точек 1 и 2 на траекториях их вращения, «вырожденных» в прямые.