Вращением вокруг проецирующих прямых можно решить все четыре основные задачи, решаемые способом дополнительного проецирования. Однако эти решения получаются более громоздкими, поэтому для примера рассмотрим только две из них – первую и третью задачи.
Пример 1 (первая задача). Превратить прямую общего положения т в прямую уровня (рисунок 83).
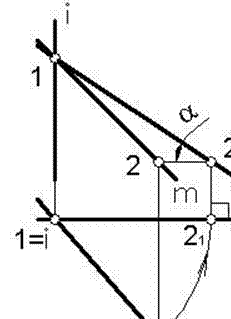 Повернем прямую т до положения фронтали. За ось вращения примем горизонтально проецирующую прямую i, проходящую через произвольную точку 1 прямой т. при повороте прямой т эта точка будет неподвижна и для поворота прямой останется повернуть лишь вторую ее точку - 2. Так как горизонтальная проекция прямой т в своем новом положении должна быть перпендикулярна линиям связи (см. 4.3), то этим определяется угол поворота точки 2. Построив новые положения проекций точки 2 (21), тем самым определим прямую т в положении фронтали. На виде спереди (фронтальной проекции) отрезок 1-21 прямой т 1 проецируется в натуральную величину, а угол α – истинный угол наклона прямой т к горизонтальной плоскости проекций.
Повернем прямую т до положения фронтали. За ось вращения примем горизонтально проецирующую прямую i, проходящую через произвольную точку 1 прямой т. при повороте прямой т эта точка будет неподвижна и для поворота прямой останется повернуть лишь вторую ее точку - 2. Так как горизонтальная проекция прямой т в своем новом положении должна быть перпендикулярна линиям связи (см. 4.3), то этим определяется угол поворота точки 2. Построив новые положения проекций точки 2 (21), тем самым определим прямую т в положении фронтали. На виде спереди (фронтальной проекции) отрезок 1-21 прямой т 1 проецируется в натуральную величину, а угол α – истинный угол наклона прямой т к горизонтальной плоскости проекций.
 Для поворота прямой до положения горизонтали нужно за ось вращения принять фронтально проецирующую прямую, проведенную через произвольную точку заданной прямой.
Для поворота прямой до положения горизонтали нужно за ось вращения принять фронтально проецирующую прямую, проведенную через произвольную точку заданной прямой.
Пример 2 (третья задача). Превратить плоскость общего положения Д (ΔАВС) в проецирующую плоскость (рисунок 84).
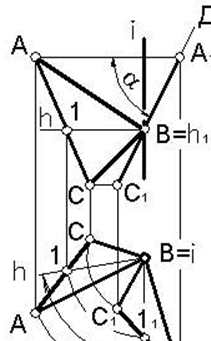
Повернем плоскость Д, например, до положения фронтально проецирующей плоскости. Для этого ее нужно повернуть вокруг горизонтально проецирующей прямой i так, чтобы горизонтали плоскости Д стали фронтально проецирующими прямыми. Поскольку при этом на виде сверху (на горизонтальной проекции) некоторая горизонталь h займет положение h 1, параллельное линиям связи, отсюда определится и угол поворота (как угол между «старым» и «новым» положениями горизонтали). Так как ось вращения проходит через одну из вершин треугольника АВС, то на этот угол остается повернуть лишь две оставшиеся вершины – А и С. Новые положения этих вершин А1 и С1 совместно с неподвижной вершиной В определят новое фронтально проецирующее положение плоскости Д. Фронтальные проекции точек плоскости Д расположатся на одной прямой, в которую “выродится” плоскость на виде спереди. Угол α между проекцией плоскости Д и прямой перпендикулярной линиям связи – есть натура угла наклона плоскости Д к горизонтальной плоскости проекций.
Для поворота плоскости Д до положения горизонтально проецирующей плоскости, нужно за ось вращения принять фронтально проецирующую прямую, проведенную через какую-нибудь точку плоскости.
Рассмотрим еще два примера применения способа вращения вокруг проецирующих прямых.
|
|
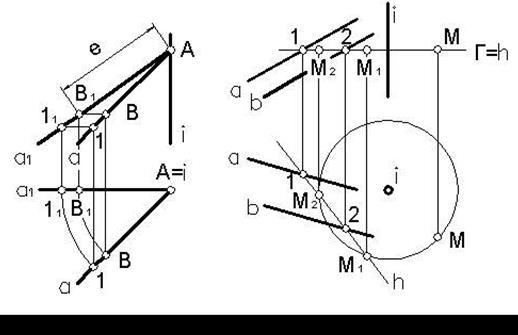 |
Пример 3. На прямой общего положения α от ее точки А отложить отрезок АВ заданной длины е (рисунок 85).
Возьмем на прямой α произвольную точку 1 (не совпадающую с точкой А). Повернем прямую α вокруг горизонтально проецирующей прямой i, проходящей через точку А, до положения фронтали. Так как на виде спереди (фронтальной проекции) в этом случае имеем натуру отрезка А-1, то, отложив на натуре отрезка А-1 отрезок АВ заданной длины е и, произведя обратный поворот, найдем на прямой α проекции искомой точки В. Нужно иметь в виду, что отрезок длиной е можно отложить на прямой α от точки А и в другую сторону.
Пример 4. Повернуть точку М вокруг горизонтально проецирующей прямой i до совмещения ее с плоскостью Б(α // b) (рисунок 86).
При вращении вокруг прямой i точка М будет описывать окружность в горизонтальной плоскости Г. Поэтому точка М окажется в плоскости Б тогда, когда она будет находиться на линии пересечения плоскостей Б и Г, т.е. на горизонтали h плоскости Б. Проведя на виде сверху (горизонтальной проекции) окружность радиуса i М, получим в пересечении ее с горизонтальной проекцией горизонтали h два новых положения точки М – М1 и М2.
В нашем случае горизонталь h пересекает окружность (траекторию вращения точки М) дважды, т.е. задача имеет два решения. Если бы горизонталь h касалась окружности – задача имела бы одно решение, а если бы проходила вне ее – это означало бы отсутствие решения.