Правила вычисления пределов
; 
; 
; 
; 
Основные пределы
Первый замечательный предел: 
Второй замечательный предел: 
или 
Вычисление пределов при 
Можно пользоваться асимптотическими формулами:
; 
; 
; 
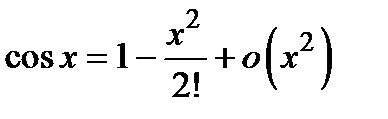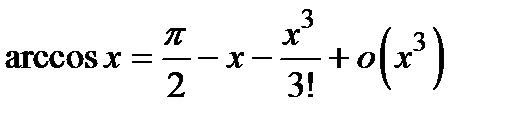
Алгоритм решения.
1. Подставить в выражение предельное значение аргумента.
2. Определить есть или нет неопределенность. Если нет, дать ответ.
3. Если неопределенность есть, то по ее виду выбрать одно из правил устранения этой неопределенности.
4. Преобразовать выражение согласно выбранному правилу, и к новой форме предела применить данный алгоритм, начиная с п.1.
Правило 1. Неопределенность типа 
: 
В числителе и знаменателе вынести 
в максимальной степени, если это возможно и сократить на него. Заметим, что 
, а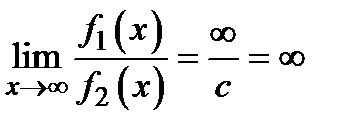 
, где c - любое число.
Правило 2. Неопределенность типа 
: 
Числитель и знаменатель разделить одновременно на 
, если это возможно.
Заметим, что 
, а 
, где c - любое число, отличное от нуля.
Правило 3. При вычислении пределов от иррациональных выражений, не попадающих в предыдущие правила, следует избавиться от корней, входящих в неопределенность. Возможны следующие способы:
1) замена переменной 
, позволяющая извлечь корни, входящие в неопределенность;
2). дополнение до формулы, позволяющей возвести корень в соответствующую ему степень;
здесь используются формулы 
; 
Правило 4. При наличии неопределенности в пределе от выражения, содержащего тригонометрические функции, следует выделить в этом выражении первый замечательный предел: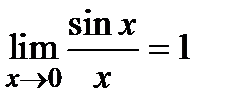 
Можно использовать следствия этого предела:
; 
: 
; 
Правило 5. Вычисление предела сложно показательной функции.
Если предел содержит неопределенность типа 
, то он сводится ко второму замечательному пределу: 
или 
Правило 6. Предел сложной функции 
.
В частности: 
, если 
Необходимо помнить свойства логарифмов:
; 
; 
; 
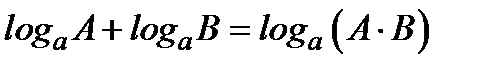Правило Лопиталя. Пусть функци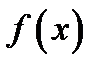и 
и 
дифференцируемы в некоторой окрестности точки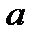 
, и пусть 
или 
. Тогда 
Коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание. Отметим, что формула справедлива только в том случае, если предел, стоящий справа, существует. Если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.
Замечание. К этим же двум случаям 
и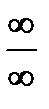 
сводятся случаи неопределенносте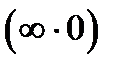й: 
и 
.
Замечание. Для раскрытия неопределенностей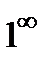 
, 
, 
нужно прологарифмировать данную функцию и найти предел ее логарифма.
Полезные формулы пределов:
; 
; 
; 
; 
; 
; 
; 
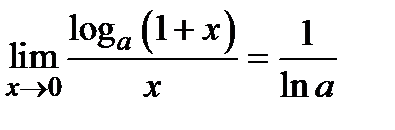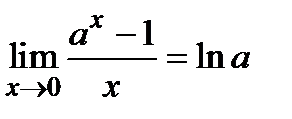
Пример. Дана функция 
. Найти предел при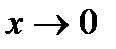 
;
Неопределенность типа 
Прологарифмируем функцию: 
;
вычислим предел логарифма:
неопределенность типа 
.
Раскрываем по Лопитилю:
Получили, что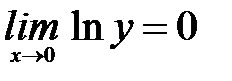 
.
Поскольку 
, то 
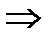
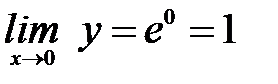
б) производную первого порядка.
Производная сложной функции: 
Производная степенно-показательной функции вычисляется путем логарифмирования:
Пример. Дана функция . Найти производную первого порядка
Логарифмируем функцию: ;
Дифференцируем левую и правую части равенства;
