Множества и операции над ними
Основные понятия о множества.
1.1. Основные определения.
Одним из основных понятий математики является понятие множества, и, как каждое основное понятие, не поддаётся точному определению (например, понятия “точка”, “прямая” являются одними из основных понятий геометрии).
МНОЖЕСТВОМ называется собрание, совокупность объектов, объединенных по какому-нибудь общему признаку, свойству.
Примеры:
1. Множество студентов данной учебной группы.
2. Множество планет солнечной системы.
3. Множество букв русского алфавита.
4. Множество натуральных чисел.
Математический смысл слова “множество” отличается от того, как оно используется в обычной речи. Так, в обычной речи понятие “множество” связывают с большим числом предметов, в математике же этого не требуется. Здесь могут рассматриваться множества, содержащие один объект, много объектов, несколько объектов или не содержащие ни одного объекта.
Объекты, из которых состоит множество, называются его ЭЛЕМЕНТАМИ.
Остановимся на символике, обычно использующейся при обращении с множествами.
Множества обозначаются прописными (заглавными) буквами латинского алфавита (без индексов или с индексами). Например: B, C,…,X,Y,…,A1,B1,…
Элементы множества обозначаются строчными (малыми) буквами латинского алфавита. Например: b,c,…,x,y,…,a1,b1,…
В математике особую роль играют множества, элементами которых являются числа. Такие множества называются ЧИСЛОВЫМИ. Некоторые числовые множества имеют специальные обозначения, вводимые для удобства пользования. Один из вариантов этих обозначений, которыми мы будем пользоваться в дальнейшем, выглядит следующим образом:
|
|
N – множество всех натуральных чисел;
Zc (или Z+ или C+) – множество всех целых неотрицательных чисел;
Z (или C) – множество всех целых чисел;
Q – множество всех рациональных чисел;
R – множество всех действительных чисел;
R+ - множество всех действительных положительных чисел.
По числу элементов, входящих в множество, множества делятся на три класса:
1 – конечные, 2 – бесконечные, 3 – пустые.
1. Если элементы множества можно сосчитать, то множество является КОНЕЧНЫМ.
Пример 1.
Множество гласных букв в слове “математика” состоит из трёх элементов – это буквы “а”, “е”, “и”, причем, гласная считается только один раз, т.е. элементы множества при перечислении не повторяются.
2. Если элементы множества сосчитать невозможно, то множество БЕСКОНЕЧНОЕ.
Пример 2.
Множество натуральных чисел бесконечно.
Пример 3.
Множество точек отрезка [0;1] бесконечно.
3. Множество, не содержащее ни одного элемента, называется ПУСТЫМ. Символически оно обозначается знаком Æ.
Пример 4.
Множество действительных корней уравнения x2 +1=0.
Пример 5.
Множество людей, проживающих на Солнце.
В математике часто приходится определять принадлежность данного элемента конкретному множеству.
Пример 6.
Мы говорим, что число 5 натуральное, т.е. утверждаем, что число 5 принадлежит множеству натуральных чисел. Символически принадлежность множеству записывается с помощью знака Î. В данном случае символическая запись будет такой: 5 Î N. Читается: “5 принадлежит множеству натуральных чисел”.
Число 5,2 не принадлежит множеству натуральных чисел, т.к. не является натуральным числом. Символически отношение “не принадлежит” записывается с помощью знака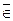 
(реже Ï). Таким образом, здесь имеем: 5,2 Ï N
|
|
Читается: “5,2 не принадлежит множеству натуральных чисел”.
Способы задания множеств.
Множество считается заданным, если мы владеем способом, позволяющим для любого данного элемента определить, принадлежит он данному множеству или не принадлежит.
Множество можно задать, непосредственно перечислив все его элементы, причём, порядок следования элементов может быть произвольным. В этом случае названия всех элементов множества записываются в строчку, отделяются точкой с запятой и заключаются в фигурные скобки.
Пример 7.
Множество всех гласных букв русского алфавита:
A={а; я; у; ю; э; е;о; ё; и; ы}.
Пример 8.
Множество цифр десятичной системы счисления:
B={1; 2; 3; 4; 5; 6; 7; 8; 9; 0}.
Очевидно, что такой способ задания множеств удобно применять для конечных множеств с небольшим количеством элементов.
Конечные и бесконечные множества могут быть заданы другим способом: указанием ХАРАКТЕРИСТИЧЕСКОГО СВОЙСТВА, т.е. такого свойства, которым обладает любой элемент данного множества и не обладает ни один элемент, не принадлежащий ему.
Пусть P обозначает некоторое свойство, которым обладают все элементы множества А и не обладают элементы никакого другого множества. Тогда множество всех элементов, обладающих свойством Р, обозначим так:
А={х│х обладает свойством Р}={ х│Р(х)}={х: Р(х)}.
Свойство Р, задающее множество А, есть характеристическое свойство множества А.
|
|
Пример 9.
Множество чётных натуральных чисел. Зададим его с помощью характеристического свойства:
В={х │х – чётное натуральное число}={х │ х=2k, k Є N}.
Пример 10.
Множество всех действительных чисел на отрезке от 1 до 3 включительно запишется следующим образом:
R1-3={y│1≤ y≤ 3, y Є R}.
Следует заметить, что в ряде случаев одно и то же множество может быть задано как первым, так и вторым способом.
Пример 11.
Множество натуральных чисел, меньших, чем 10.
Первый способ: N<10={1; 2; 3; 4; 5; 6; 7; 8; 9}.
Второй способ: N<10={z│z<10, z Є N}.
Случается, что одно и то же множество может быть задано с помощью различных характеристических свойств.
Пример 12.
Множество квадратов.
Первый способ: A={x│x – ромб с прямыми углами}.
Второй способ: A={ x│x – прямоугольник с равными сторонами}.