Содержание задачи.
Рассматривая понтон как цилиндр, находящийся в безграничной идеальной жидкости (рис.4), однородный поток который набегает на него перпендикулярно оси симметрии со скоростью V0, построить картину линий тока течения для поперечного сечения цилиндра, пренебрегая конечностью его размаха.

Рис. 4
Найти также распределение гидродинамического давления по цилиндру и построить эпюру скоростей в точках оси Оу. Плотность жидкости принять равной плотности воды. При построении линий тока течения промежутки между соседними линиями тока следует выбирать из условия:
 , где
, где  – разность значений функции тока
– разность значений функции тока 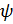 на соседних линиях тока.
на соседних линиях тока.
Ориентировочные размеры картины линий тока: ± 2D относительно оси Oy и ± 1,5D относительно Oх.
2. Исходные данные и принятые приложения.
Длина понтона, L, м 44
Диаметр понтона, D, м 8
Скорость набегающего потока жидкости, V0, м/с 12
Ускорение свободного падения, g, м/сек2 9,81
Положение понтона в воде см.рис.4
Плотность воды, р, m/м3 1,025
В данной задаче рассматривается обтекание кругового цилиндра в безграничной идеальной жидкости, где из массовых тел действует лишь сила тяжести.
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
| Лист |
| КР.ГМХ.260302.22 |
Определение потенциала скоростей и функций тока
Потенциал скорости потока, который набегает на цилиндр, будет равен сумме потенциалов скорости равномерного потока и плоского диполя:
φ = φ1+ φ2
ψ = ψ1+ ψ2
φ – потенциал скорости
ψ – функция тока
Выразим потенциал скорости и функцию тока:
φ = (V  r +
r +  )*cos θ
)*cos θ
ψ = (V  r -
r -  )*sin θ
)*sin θ
V  - скорость потока на бесконечном удалении от цилиндра (учитывая условия задачи, V
- скорость потока на бесконечном удалении от цилиндра (учитывая условия задачи, V  V0)
V0)
M – момент диполя:
М =  · V
· V  · r02
· r02
r0 – радиус цилиндра ( = 4)
= 4)
θ – угол между радиус-вектором, соединяющим рассматриваемую точку и начало системы координат, и осью OX.
Подставляем выражение момент диполя в выражения для нахождения φ и ψ:
φ = 

| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
| Лист |
| КР.ГМХ.260302.22 |
Скорость потока можно представить в виде суммы радиальной (vr) и окружной (vθ) скоростей:

Величины vr и vθ определяем по формулам:
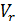 =
=  =
= 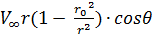
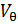 =
=  *
*  = -
= - 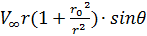
Построение системы линий тока
Уравнение семейства линии тока:
ψ = С
С – константа, характеризующая местоположение каждой точки линии тока в пространстве;
Таким образом преобразованная формула для определения функции тока будет иметь вид:
С = 
Учитывая начальные условия задачи, линия тока необходимо выстраивать с определенным промежутком между соседними линиями тока, а именно:
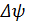 =
=  ·v0
·v0
 разность значений функций тока ψ на соседних линиях тока.
разность значений функций тока ψ на соседних линиях тока.
Таким образом, начальное значение:
С= 0
Изменяем с шагом:
 = 24 (м2/c)
= 24 (м2/c)
Для построения линий тока используем выражение С =  , которое разрешим относительно переменной r (переменную
, которое разрешим относительно переменной r (переменную  будем задавать с шагом в 10 градусов):
будем задавать с шагом в 10 градусов):
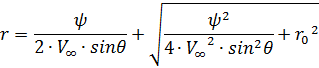
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
| Лист |
| КР.ГМХ.260302.22 |
Результаты расчетов (табл.1)
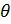
| |||||||||||
Значения
функции
тока
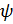 , м2/с , м2/с
| |||||||||||

| 12,78 | 7,87 | 6,47 | 5,85 | 5,5 | 5,31 | 5,2 | 5,13 | 5,12 | ||

| 23,74 | 12,92 | 9,65 | 8,17 | 7,38 | 6,92 | 6,66 | 6,51 | 6,47 | ||

| 35,05 | 18,41 | 13,21 | 10,8 | 9,5 | 8,75 | 8,3 | 8,06 | |||

| 46,47 | 24,05 | 16,94 | 13,62 | 11,79 | 10,72 | 10,09 | 9,76 | 9,65 | ||

| 57,94 | 29,76 | 20,77 | 16,51 | 14,17 | 12,8 | 11,97 | 11,53 | 11,46 | ||

| 69,43 | 35,54 | 24,65 | 19,48 | 16,63 | 14,92 | 13,37 | 13,22 |
По найденным данным построим картину линий тока (см. рис.4.1).

| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
| Лист |
| КР.ГМХ.260302.22 |
В точках на оси OY угол θ = ±90. Таким образом:
sin θ = ±1
cos θ = 0
Следовательно, выражение скорости в точках оси OY будет иметь следующий вид:
vr = 0

Расчеты (табл.2)
| r,м | |||||||||
| V,м/c | 21,6 | 19,92 | 18,84 | 17,3 | 16,8 | 16,32 |
По найденным данным построим эпюру скоростей (см. рис 4.2).