Теоретический материал для самостоятельного изучения
Двугранный угол — это часть пространства, заключённая между двумя полуплоскостями, имеющими одну общую границу.

Если в пространстве пересекаются две плоскости, получаются четыре двугранных угла (аналогично как при пересечении двух прямых получаются четыре угла). Рассмотрим один из них.

Полуплоскости α и β, образующие двугранный угол, называются его гранями.
Общая прямая a этих граней называется ребром двугранного угла.
Выберем на ребре a двугранного угла произвольную точку C и проведём две пересекающиеся прямые AC⊥a и BC⊥a, а через эти прямые — плоскость γ перпендикулярно ребру a.

Линии пересечения AC и BC полуплоскостей α и β с плоскостью γ образуют некоторый угол ∡ACB. Этот угол называется линейным углом двугранного угла. Величина линейного угла не зависит от выбора точки C на ребре a.
Величина двугранного угла 0°< ∡ACB <180°.
Если плоскости параллельны, то угол между ними равен 0° по определению.
Если при пересечении плоскостей один из двугранных углов составляет 90°, то три остальных угла — тоже 90°. Эти плоскости называют перпендикулярными.
Следующие теоремы, которые здесь приведём без доказательств, могут пригодиться при решении задач.
1. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
2. Плоскость, перпендикулярная прямой, по которой пересекаются две плоскости, перпендикулярна каждой из этих плоскостей.
3. Если две плоскости перпендикулярны, и в одной из них прямая проведена перпендикулярно линии пересечения плоскостей, то эта прямая перпендикулярна второй плоскости.
Многогранные углы
Объясним понятие многогранных углов.
Представим несколько лучей в пространстве с общим началом. Их можно представить тоже как часть линий пересечения плоскостей — трёх, четырёх или больше — и назвать рёбрами многогранного угла.
 Трёхгранный угол
Трёхгранный угол
 Четырёхгранный угол
Четырёхгранный угол
 Пятигранный угол
Пятигранный угол
Каждые два луча образуют угол, который называют плоским углом многогранного угла.
Каждый плоский угол трёхгранного угла меньше суммы двух других плоских углов.
Сумма плоских углов многогранного угла меньше 360°.
Признак перпендикулярности 2-х плоскостей.
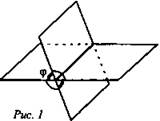
При пересечении двух плоскостей образуются четыре двугранных угла. Углом между пересекающимися плоскостями называется линейный угол φ этого двугранного угла, который 0° < φ ≤ 90° (рис. 1).
Если φ = 90°, то плоскости называются перпендикулярными (взаимно перпендикулярными) (рис. 2).
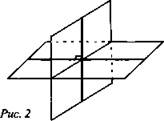
Ясно, что в этих случаях каждый из четырех двугранных углов, образованных пересекающимися плоскостями, прямой (рис. 2). Рассмотрим признак перпендикулярности двух плоскостей.
Теорема: Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Дано: α, β, АВ лежит в плоскости α, АВ ⊥ β, АВ ∩ α = А (рис. 3).
Доказать: α ⊥ β.
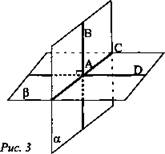
Доказательство: α ∩ β = АС, АВ ⊥ АС, так как АВ ⊥ β по условию. Проведем в плоскости βAD ⊥ AC. ∠BAD - линейный угол двугранного угла. Но ∠BAD =90°, так как ВА ⊥ β. Значит, α⊥ β. Запишите теорему и её доказательство в тетради и сделайте чертёж.
При решении задач используются утверждения:
1. Плоскость, перпендикулярная к ребру двугранного угла, перпендикулярна к его граням (следствие).
2. Перпендикуляр, проведенный из любой точки одной из двух взаимно перпендикулярных плоскостей к линии их пересечения, есть перпендикуляр к другой плоскости (№ 178).