Параллелепипедом называется призма, основанием которой служит параллелограмм.
Параллелограммы, из которых составлен параллелепипед, называются его гранями, их стороны — ребрами, а вершины параллелограммов — вершинами параллелепипеда. У параллелепипеда все грани — параллелограммы.
Параллелепипеды могут быть прямые и наклонные.
Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани — боковыми гранями параллелепипеда. Ребра параллелепипеда, не принадлежащие основаниям, называют боковыми ребрами.
Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих ребер —противоположными.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда.
Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани — прямоугольники.
Длины не параллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями). У прямоугольного параллелепипеда три линейных размера.
Свойства параллелепипеда:
- Противоположные грани параллелепипеда равны и параллельны.
- Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
- Боковые грани прямого параллелепипеда — прямоугольники.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. d 2 = a 2 + b 2 + c 2.
Решение задач из учебника:
№172
Дано: ΔАВС, ∠С = 90°, АС лежит в плоскости α, угол между плоскостями α и ABCравен 60°, АС = 5 см, АВ = 13 см (рис. 4).Найти: расстояние от точки В до плоскости α.
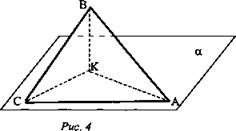
Решение: Построим ВК ⊥ α. Тогда КС - проекция ВС на эту плоскость. ВС ⊥ АС по условию, значит, по теореме о трех перпендикулярах, КС ⊥ АС. Отсюда следует, что ∠ВСК - линейный угол двугранного угла между плоскостью α и плоскостью треугольника, ∠ВСК = 60°. Из ΔВСА по теореме Пифагора: 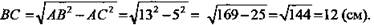
Из ΔВКС: 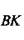
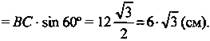
Ответ: 6√3 см.
№184.
Общая сторона АВ треугольников АВС и АВD равна 10 см. Плоскости этих треугольников взаимно перпендикулярны. Найти СD, если треугольники: а) равносторонние; б) прямоугольные равнобедренные с гипотенузой АВ.
Дано: АВ = 10 см, ΔАВС, ΔАВD. 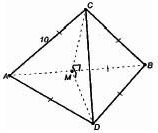
а) Построим СМ⊥АВ и отрезок МD.
В равностороннем ΔАВС: СМ – высота, а значит, и медиана, АМ = МВ = 5 см.
В ΔАВD: МD – медиана и высота, то есть МD⊥АВ.
∠СМD – линейный угол внутреннего угла САВD, ∠СМD= 90°.
СМ = 10sin60° = 5, MD = 5 (cм).
СD = (по теореме Пифагора для ΔСМD).
б) Построим СМ⊥АВ. 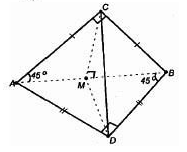
В равностороннем ΔАСВ: СМ – высота, а значит, и медиана.
Проводим отрезок DM, DM – медиана в равнобедренном ΔАВD, следовательно, и высота МD⊥АВ.
Очевидно, СМ = МА = 5 см, МD = 5 см, СD = 5 см (по теореме Пифагора для ΔСМD).
Ответ: а); б) 5 (cм).
Из дидактических материалов:
1) Два правильных треугольника АВС и BDC расположены так, что их плоскости взаимно перпендикулярны. Найдите тангенс двугранного угла, образованного плоскостями ADC и ABC.
Дано: ΔАВС и ΔDВС – правильные, (АВС) ⊥ (DВС). 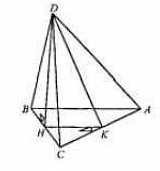
Найти: tg(∠(АВС) ⊥ (ADС)).
Решение:
DH⊥AC, HK⊥AC, следовательно, по ТТП, DK⊥AC.
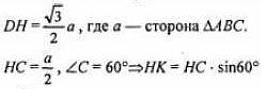
Где
Ответ: 2.
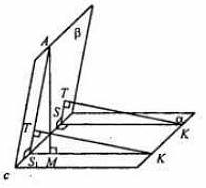
2)На гранях двугранного угла взяты 2 точки, удаленные от ребра двугранного угла на 6 и 10 см. Известно, что одна из этих точек удалена от второй грани на 7,5 см. Найти расстояние от другой точки до противоположной грани двугранного угла.
Дано: А и К лежат на разных гранях двугранного угла с ребром С. ρ(С, А) = 6, ρ(С, К) = 10, ρ(К, β) = 7,5.
Найти: ρ(А, α) =?
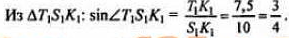
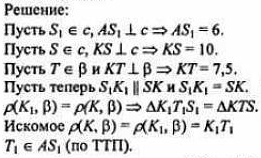
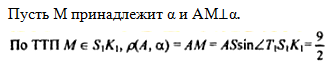
Ответ: 4,5.