Педагогическая ситуация по математике

Ответ.
В чем состоит данный метод решения систем?
В том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.
Для каких систем он применяется?
Для систем линейных алгебраических уравнений (линейная система, также употребляются аббревиатуры СЛАУ, СЛУ) – система уравнений, каждое уравнение в которой является линейным – алгебраическим уравнением первой степени.
Под каким названием он больше известен в курсе высшей математике?
Метод Гаусса. Назван в честь немецкого математика Карла Фридриха Гаусса.
С чем, на Ваш взгляд, могут быть связаны трудности школьника при его применении?
Возможные трудности:
1. При последовательном исключении переменных, если не правильно применить перемещение строк или же неправильно отнять строки или столбцы друг от друга;
2. Это не является обязательным, но при приведении к треугольному виду желательно организовывать 1 или -1 верхнем углу матрицы, чтобы не совершать операции с большими числами, иначе высока вероятность ошибиться;
3. При смене местами столбцов, необходимо помнить, что меняются вместе с ними и положение неизвестных (x, y, z). Желательно столбцы подписать x, y, z, чтобы не запутаться и правильно написать эквивалентную систему.
3. Решение системы методом последовательного исключения неизвестных:
1. Запишем расширенную матицу:
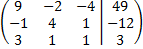
2. С помощью элементарных преобразований приведем матрицу к ступенчатому (треугольному) виду.
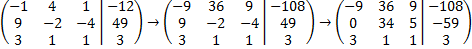 или
или 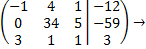
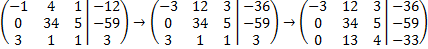 или
или 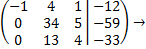
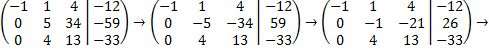
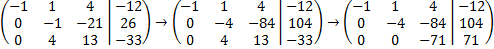
3. В результате элементарных преобразований получена эквивалентная исходной система уравнений:
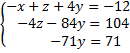
4. Найдем неизвестные. Ответ: x=3, y= –1, z= –5.
Составьте для школьника «памятнику» применения метода последовательного исключения неизвестных на примере решенной системы.
Памятка.
1. Обратить внимание на расположение неизвестных в системе уравнений: каждая неизвестная одного уравнения должная располагаться в один столбец с той же неизвестной в остальных уравнениях:
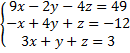
2. Выписать расширенную матрицу:
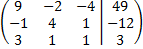
Для справки: если речь идет об обычной матрице системы, то в этом случае записываются только коэффициенты при неизвестных (свободные члены, которые находятся за вертикальной (разделительной) чертой, не записываются и сама черта в том числе!).
3. Подписать столбцы соответственно обозначениям их неизвестных (дальше обозначения писать не буду, запомните или запишите сами):
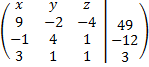
4. Привести матрицу к (верхнему или нижнему) треугольному виду. Для определенности приедем к верхнему треугольному виду, когда нули находятся ПОД главной диагональю:
4.1. Приведем матрицу к удобному виду – верхнем левом углу организуем 1 или -1 (это не обязательно, но желательно), поменяв местами верхние две строки:
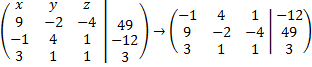
4.2. В первом столбце вместо двух нижних чисел (9 и 3) необходимо получить нули. Начинаем работать со второй строки – организуем ноль на позиции 9. Для этого умножим первую строку на 9 и прибавим ее ко второй строке:
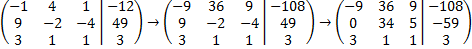 или
или 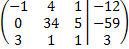
4.3. Теперь организуем ноль на позиции 3 в первом столбце. Для этого умножим первую строку на 3 и прибавим ее к третей строке:
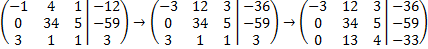 или
или 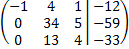
4.3. Организуем 1 или -1 на следующей «ступени», на позиции 34. Помним, что первый столбец это коэффициенты при x, второй – коэффициенты при y, третий – коэффициенты при z. Поменяем местами второй и третий столбцы. Умножим вторую строку на -1 и прибавим к ней третью.
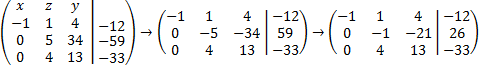
4.4. Заключительный этап элементарных преобразований. На нем нужно получить еще один 0 на позиции 4 (второй столбец, третья строка). Для этого умножим вторую строку на 4 и прибавим ее к третей строке:
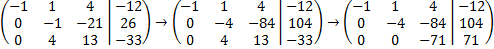
Конечная расширенная матрица и будет треугольным видом начальной.
5. Запишем эквивалентную исходной систему уравнений:
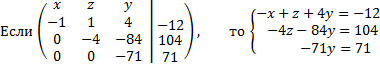
5.1. Найдем неизвестные:
Из уравнения третьего уравнения y= –1.
Подставим y во второе уравнение, находим, что z= –5.
Подставляя найденные значения z и y в первое уравнение, находим, что x=3.
Ответ: x=3, y= –1, z= –5.
| Выполним проверку. | |
| 1. По эквивалентной системе: | 2. По исходной системе: |
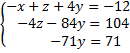 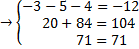 Верно.
Верно.
|
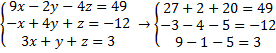 Верно.
Верно.
|
| Вывод: система методом Гаусса решена верно. |
Выделите возможные ошибки. Возможны те же ошибки, которые приведены во втором пункте вопроса.