Определение сил и моментов инерции

Силовой расчет рычажного механизма

Определение ускорений

Для расчетного положения строю план ускорений.

Ускорение точки A:

(3.1)

где a_A – ускорение точки А, м/с.

Принимаю ускорение точки А на чертеже равное 180 мм. Тогда:

(3.2)

где µ_а – масштабный коэффициент скоростей, ;

πa – длина вектора ускорения на чертеже, мм.

Определяю ускорение точки В.

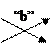
2 звено 3 звено			() ()	(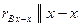3.3)
,

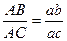
Аналогично ускорение точки D.

4 звено 5 звено		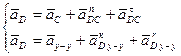	() ()	(3.4)
,

Определяю ускорения точек и тангенциальные составляющие ускорений звеньев расчетного положение рычажного механизма:

(3.5)

где а_т(зв) – ускорение точки (звена), м/с²;

– длина вектора ускорения точки (звена) на чертеже, мм.

Аналогично определяю остальные ускорения.

Таблица 3.1 Ускорения и их составляющие

Ускорение
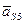
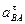
Значение на чертеже, мм
Значение ускорения, м/с2	1810.9	1074.9	497.5	1870.6		1890.5

Угловые ускорения определяются по формуле:

(3.6)

где ε_зв – угловое ускорение звена, с^-2.

Определение сил и моментов инерции

Силы инерции определяются по формуле:

(3.7)

где P_{и i} – сила инерции i-го звена, Н;

m _i – масса i-го звена, кг.

Сила инерции звена 2 будет равна:

Аналогично определяю силы инерции остальных звеньев.

Моменты инерции определяются по формуле:

(3.8)

где М_{и i} – сила инерции i-го звена, Н·м;

Момент инерции звена 2 будет равен:

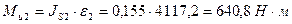
Аналогично определяю моменты инерции остальных звеньев.

 

 

Таблица 3.2 Силы и моменты инерции звеньев

Звено	2	3	4	5
Сила инерции Pи, Н	27612.5	18953,1	14013.8
Момент инерции Ми, Н·м	640,8	—	614,4	—

3.3 Определение реакций в кинематических парах и уравновешивающей силы методом планов сил

Рассмотрю группу Ассура 4-5.

Тангенциальную реакцию определяю из условия для звена 4:

(3.9)

Откуда получаю:

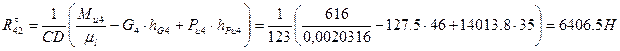
Нормальную реакцию 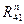определяю графически из условия :

(3.10)

Определю масштабный коэффициент плана сил группы 4-5:

(3.11)

где – масштабный коэффициент плана сил группы 4-5, ;

– сила, имеющее наибольшее из известных значений, Н;

– длина вектора силы , принятая на чертеже, мм.

Значение силы, если известна длина ее вектора, определяется по формуле:

(3.12)

где R – определяемое значение силы, Н;

– длина вектора силы P на чертеже, мм.

По формуле 3.12 определяю значения реакци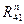й и :

 

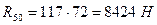
Таблица 3.3 Силы, реакции и их векторы для группы Асура 4-5

Сила
Значение силы R, Н	6406.5	149.1		255.1
Значение на чертеже , мм

Реакция будет равна . На чертеже реакция равна 230 мм.

 

Тогда по формуле 3.12 определяю:

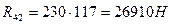
Рассмотрю группу Ассура 2-3.

Тангенциальную реакцию определяю из условия для звена 2:

(3.13)

Откуда получаю:

Нормальную реакцию определяю графически из условия :

(3.14)

Определю масштабный коэффициент плана сил группы 2-3:

(3.15)

где – масштабный коэффициент плана сил группы 2-3, ;

– сила, имеющее наибольшее из известных значений, Н;

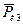– длина вектора силы , принятая на чертеже, мм.

По формуле 3.12 определяю значения реакций и :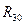

 

 

Таблица 3.3 Силы, реакции и их векторы для группы Асура 2-3

Сила
Значение силы R, Н		149.1	27612.5	99,1
Значение на чертеже , мм

Реакция будет равна . На чертеже реакция равна 140 мм.

Тогда по формуле 3.12 определяю:

Рассмотрю начальный механизм.

Уравновешивающую силу определяю из условия :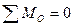

(3.16)

Откуда получаю:

Нормальную реакцию определяю графически из условия :

Определю масштабный коэффициент плана сил начального механизма:

Сила
Значение силы R, Н
Значение силы на чертеже , мм

Реакция будет равна: