Таблица 2.3
Вычисление среднего арифметического значения признака для вариационного ряда распределения курсовой цены акции, тыс.руб.

| 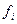
| Середина интервала (тыс.руб.), 
| 
|
| 20-51 | 35,5 | 603,5 | |
| 51-82 | 66,5 | 1263,5 | |
| 82-113 | 97,5 | ||
| 113-144 | 128,5 | 385,5 | |
| 144-175 | 159,5 | 797,5 | |
| Итого |
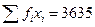



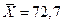 тыс.руб.– среднее значение курсовой цены акций, тыс.руб.
тыс.руб.– среднее значение курсовой цены акций, тыс.руб.
Таблица 2.4
Вычисление среднего арифметического значения признака для вариационного ряда распределения дивидендов, начисленных по результатам деятельности, тыс.руб.

| 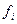
| Середина интервала (тыс.руб.), 
| 
|
| 17-18,333 | 17,6665 | 229,665 | |
| 18,333-19,666 | 18,9995 | 151,996 | |
| 19,666-20,999 | 20,3325 | 162,66 | |
| 20,999-22,332 | 21,6655 | 281,652 | |
| 22,332-23,665 | 22,9985 | 68,996 | |
| 23,665-25 | 24,3325 | 121,663 | |
| Итого | 1016,632 |




 тыс.руб.– среднее значение дивиденда, начисленного по результатам деятельности, тыс.руб.
тыс.руб.– среднее значение дивиденда, начисленного по результатам деятельности, тыс.руб.
Мода (М о ) – наиболее часто встречающееся значение признака в совокупности.
Если ряд равноинтервальный, то используется формула:

где
 – начало интервала, содержащего моду,
– начало интервала, содержащего моду,
 - величина интервала, содержащего моду,
- величина интервала, содержащего моду,
 - частота того интервала, в котором расположена мода,
- частота того интервала, в котором расположена мода,
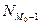 – частота интервала, предшествующего модальному,
– частота интервала, предшествующего модальному,
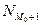 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
Таблица 2.5
Вычисление моды показателей курсовой цены акций, тыс.руб.

| 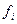
|
| 20-51 | |
| 51-82 | |
| 82-113 | |
| 113-144 | |
| 144-175 | |
| Итого |
Второй интервал содержит моду, значит:
 тыс.руб.
тыс.руб.
 тыс.руб.
тыс.руб.


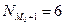
Подставим эти данные в формулу вычисления моды:
 тыс.руб.
тыс.руб.
Таблица 2.6
Вычисление моды для дивидендов, начисленных по результатам деятельности, тыс.руб.

| 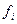
|
| 17-18,333 | |
| 18,333-19,666 | |
| 19,666-20,999 | |
| 20,999-22,332 | |
| 22,332-23,665 | |
| 23,665-25 | |
| Итого |
 тыс.руб.
тыс.руб.
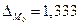 тыс.руб.
тыс.руб.
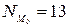
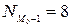
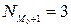
Подставим эти данные в формулу вычисления моды:
 тыс.руб.
тыс.руб.
Вывод: большинство предприятий имеют значения курсовой цены акции около 55,135 тыс.руб., значения дивидендов, начисленных по результатам деятельности, тыс.руб. у большинства предприятий около 21,444 тыс.руб.
Медиана (Ме ) – это такое значение признака, которое делит объем совокупности пополам в том смысле, что число элементов совокупности с индивидуальными значениями признака, меньшими медианы, равна числу элементов совокупности с индивидуальными значениями больше медианы.
Численное значение медианы определяется по ряду накопленных частот.

 ,
,
где
 – начало интервала, содержащего медиану,
– начало интервала, содержащего медиану,
 – величина интервала, содержащего медиану,
– величина интервала, содержащего медиану,
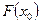 – накопленная частота на начало интервала, содержащего медиану,
– накопленная частота на начало интервала, содержащего медиану,
 – объем совокупности,
– объем совокупности,
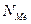 – частота того интервала, в котором расположена медиана.
– частота того интервала, в котором расположена медиана.
Таблица 2.7
Вычисление медианы для курсовой цены акции, тыс.руб.

| 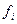
| Показатель накопленной частоты |
| 20-51 | ||
| 51-82 | ||
| 82-113 | ||
| 113-144 | ||
| 144-175 | ||
| Итого |
50/2=25. Значит, медиана находится во втором интервале.
 тыс.руб.
тыс.руб.
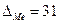 тыс.руб.
тыс.руб.

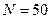

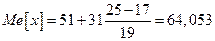 тыс.руб.
тыс.руб.
Таблица 2.8
Вычисление медианы для дивидендов, начисленных по результатам деятельности, тыс.руб.

| 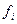
| Показатель накопленной частоты, |
| 17-18,333 | ||
| 18,333-19,666 | ||
| 19,666-20,999 | ||
| 20,999-22,332 | ||
| 22,3332-23,665 | ||
| 23,665-25 | ||
| Итого |
 тыс.руб.
тыс.руб.
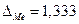 тыс.руб.
тыс.руб.

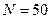


 тыс.руб.
тыс.руб.
Вывод: половина предприятий имеют значение курсовой цены акции меньше 64,053 тыс.руб., другая – больше 64,053 тыс.руб.
Половина предприятий имеют значение дивидендов, начисленных по результатам деятельности меньше 20,333 тыс.руб., другая – больше 20,333 тыс.руб.
Дисперсия ( ) – это среднее из квадратов отклонений от средней величины, для вариационного ряда она определяется по формуле:
) – это среднее из квадратов отклонений от средней величины, для вариационного ряда она определяется по формуле:
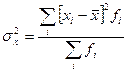
Если ряд интервальный, то в качестве варианты (xi), также как при расчете средней, берется середина интервала.
Среднее квадратическое отклонение ( ) – показатель, который представляет собой квадратный корень из дисперсии. Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения и выражается в тех же единицах, что и варианты признака.
) – показатель, который представляет собой квадратный корень из дисперсии. Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения и выражается в тех же единицах, что и варианты признака.
Таблица 2.9
Вычисление среднего квадратического отклонения для курсовой цены акции, тыс.руб.
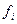
| Середина интервала (тыс.руб.), 
| 
| 
| 
|
| 35,5 | -37,2 | 1383,84 | 23525,28 | |
| 66,5 | -6,2 | 38,44 | 730,36 | |
| 97,5 | 24,8 | 615,04 | 3690,24 | |
| 128,5 | 55,8 | 3113,64 | 9340,92 | |
| 159,5 | 86,8 | 7534,24 | 37671,2 | |

 тыс.руб.
тыс.руб.
Таблица 2.10
Вычисление среднего квадратического отклонения дивидендов, начисленных по результатам деятельности, тыс.руб.
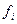
| Середина интервала (тыс.руб.), 
| 
| 
| 
|
| 17,6665 | -2,6665 | 7,110 | 92,43 | |
| 18,9995 | -1,3335 | 1,7782 | 14,23 | |
| 20,3325 | -0,0005 | 0,00000025 | 0,000002 | |
| 21,6655 | 1,3325 | 1,7755 | 23,082 | |
| 22,9985 | 2,6655 | 7,1049 | 21,315 | |
| 24,3325 | 3,9995 | 15,996 | 79,98 | |
| 231,07 |

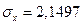 тыс.руб.
тыс.руб.
Вывод: по полученным данным среднего квадратического отклонения можно сделать вывод об однородности исследуемых совокупностей. Первая совокупность (курсовая цена акций, тыс.руб.) неоднородна. А вторая (дивиденды, начисленные по результатам деятельности, тыс.руб.) – однородна. Среднее квадратическое отклонение – мерило надежности средней: чем меньше среднее квадратическое отклонение, тем лучше среднее арифметическое отражает собой всю представленную совокупность.
Коэффициент вариации (V) – относительный показатель колеблемости признака в данной совокупности.
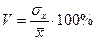
Он позволяет сравнивать вариации различных признаков, а также одноименных признаков в разных совокупностях. Его используют для характеристики однородности совокупности.
Для значений курсовой цены акций, тыс.руб.:


Для значений дебиторской задолженности на конец года, тыс.руб.:


Вывод: совокупность считается количественно однородной, если коэффициент вариации не превышает 33%. По нашим расчетам имеющиеся совокупности неодинаковы. Колеблемость признака в совокупности признак-фактора составляет 52,26% (совокупность неоднородна), признак-результата – 10,57% (совокупность однородна).
Задание № 3
Пользуясь табл. 2 и 3, сформировать таблицу исходных данных. Определить индивидуальные индексы:
• физического объема,
• цены;
• стоимости.
Определить общие индексы:
• физического объема,
• цены;
• стоимости.
Объяснить экономический смысл каждого из индексов, показать взаимосвязь между ними.
Определить абсолютное изменение стоимости произведенной продукции в текущем периоде по сравнению с базисным, в том числе за счет изменения цен и за счет изменения выпуска продукции.
Считая продукцию однородной, определить, как изменилась средняя цена единицы продукции и как при этом повлияло изменение цен и изменение структуры выпускаемой продукции. Объяснить полученные результаты.
Используя данные табл. 5, рассчитать, как в среднем изменилась себестоимость единицы и выпуск продукции.
Таблица 2
| Базисный период | Текущий период | |||
| Вид продукции | Выпуск продукции, тыс. шт. | Цена за единицу, тыс. руб./шт. | Выпуск продукции, тыс. шт. | Цена за единицу, тыс. руб./шт. |
| А | Г | |||
| I II III |
Решение:
Формируем таблицу исходных данных.
Таблица 3.1.
| Вид продукции | Базисный период | Текущий период | Индиви-дуальный индекс физиче-ского объема | Индиви-дуальный индекс цены | Индиви-дуальный индекс стоимости | Стоимость продукции в сопоставимых ценах, тыс.руб. | ||||
| Выпуск продукции, тыс.шт | Цена за единицу, тыс.руб./ шт | Стои мость продук ции, тыс.руб. | Выпуск продук ции, тыс.шт | Цена за единицу, тыс.руб./шт | Стоимость продук ции, тыс.руб. | |||||

| 
| 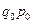
| 
| 
| 
| 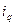
| 
| 
| 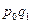
| |
| І | 0,9509 | 1,05 | 1,0052 | |||||||
| ІІ | 1,9048 | 1,154 | 2,1978 | |||||||
| ІІІ | 1,2 | 1,2 | ||||||||
| Итого: |
Индивидуальный индекс физического объема показывает как изменится объем выпуска продукции в текущем периоде по сравнению с базисным по каждому виду продукции и рассчитывается по формуле:
 .
.
В нашем случае объем выпуска продукции І вида уменьшился в текущем периоде по сравнению с базисным на 4,9%, по второму виду увеличился на 90,4%, по третьему виду объем выпуска продукции не изменился.
Индивидуальный индекс цены рассчитывается по формуле: 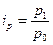 и показывает как изменились цены по каждому виду продукции. У нас по всем трем видам продукции произошло увеличение цен на 5,72%, 15,39 % и 20% соответственно.
и показывает как изменились цены по каждому виду продукции. У нас по всем трем видам продукции произошло увеличение цен на 5,72%, 15,39 % и 20% соответственно.
Индивидуальный индекс стоимости показывает изменение стоимости продукции по ее видам и рассчитывается по формуле: 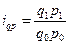 . Таким образом по всем видам продукции произошло увеличение на 0,52%, 119,78% и 20% соответственно.
. Таким образом по всем видам продукции произошло увеличение на 0,52%, 119,78% и 20% соответственно.
Общий индекс физического объема будет иметь вид:
 или 117,3%,
или 117,3%,
Т.е. выпуск продукции в текущем периоде по сравнению с базисным увеличился на 17,3%.
Общий индекс цены показывает как в целом на предприятии изменились цены на продукцию и рассчитывается по формуле:
 или 116,2%,
или 116,2%,
Т.е. цены на всю продукцию предприятия в текущем периоде по сравнению с базисным увеличились на 16,2%.
Общий индекс стоимости показывает как в среднем изменилась стоимость продукции в текущем периоде по сравнению с базисным и рассчитывается по формуле:
 или 136,3%,
или 136,3%,
Т.е. стоимость продукции в среднем по предприятию увеличилась на 36,3% в текущем периоде по сравнению с базисным.
Проверка: 
Абсолютное изменение стоимости произведенной продукции в текущем периоде по сравнению с базисным определяется по формуле:
 тыс.руб.
тыс.руб.
в том числе:
· За счет изменения цен на отдельные виды продукции
 тыс.руб.
тыс.руб.
· За счет изменения физического объема продукции
 тыс.руб.
тыс.руб.
Проверка: 2056 + 1817 =3927 тыс.руб.
Таким образом, увеличение стоимости продукции в текущем периоде по сравнению с базисным на 3927 тыс.руб. произошло в основном за счет увеличения цен на отдельные виды продукции (2056 тыс.руб.), а за счет изменения объема выпускаемой продукции ее стоимость увеличилась на 1871 тыс.руб.
Изменение средней цены единицы продукции определяем, считая эту продукцию однородной, следовательно:

Т.е. средняя цена единицы продукции увеличилась в текущем периоде по сравнению с базисным на 12,8%. В том числе а) за счет непосредственного изменения цен на отдельные виды продукции:
 , цена увеличилась на 16,2% за счет повышения цен и структурного сдвига.
, цена увеличилась на 16,2% за счет повышения цен и структурного сдвига.
За счет изменения структуры (объема) продукции:
 , средняя цена на продукцию предприятия уменьшилась на 3 % за счет изменения объема продукции.
, средняя цена на продукцию предприятия уменьшилась на 3 % за счет изменения объема продукции.
Проверка: 1,162*0,9707=1,128
Сформируем таблицу, используя таблицу 5 задания.
| Вид продукции | Изменения стоимости в текущем периоде по сравнению с базисным (%) | Изменение физического объема продукции в текущем периоде по сравнению с базисным | Затраты на продукцию | |
| Базисный период | Текущий период | |||
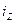
| 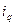
|  
|  
| |
| А | ||||
| В | ||||
| С | ||||
| Сумма |
Определим как изменилась себестоимость произведенной продукции в текущем периоде по сравнению с базисным.
 , т.е. себестоимость продукции уменьшилась в текущем периоде по сравнению с базисным на 3,96%.
, т.е. себестоимость продукции уменьшилась в текущем периоде по сравнению с базисным на 3,96%.
Определим как изменился выпуск продукции в текущем периоде по сравнению с базисным:
 , т.е. выпуск продукции увеличился в текущем периоде по сравнению с базисным на 14,85 %.
, т.е. выпуск продукции увеличился в текущем периоде по сравнению с базисным на 14,85 %.
Задание № 4
1. Используя результаты расчетов, выполненных в задании № 2 контрольной работы 1 по признаку 1, и полагая, что эти данные получены при помощи собственно случайного 10 %-го бесповторного отбора, определить:
а) пределы, за которые с доверительной вероятностью 0,954 не выйдет среднее значение признака, рассчитанное по генеральной совокупности;
б) как нужно изменить объем выборки, чтобы снизить предельную ошибку средней величины на 50 %.
2. Используя результаты расчетов, выполненных в задании № 2 контрольной работы 1 по признаку 2, и полагая, что эти данные получены при помощи повторного отбора, определить:
а) пределы, за которые в генеральной совокупности не выйдет значение доли предприятий, у которых индивидуальные значения признака превышают моду (уровень доверительной вероятности установите по своему усмотрению);
б) как изменить объем выборки, чтобы снизить предельную ошибку доли на 20 %.
Решение:
Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются средней ошибкой выборки, которая представляет собой среднее квадратическое отклонение возможных значений выборочных характеристик (оценок) от генеральных. Она определяется в зависимости от метода отбора.
При бесповторном отборе, при котором повторное попадание в выборку одних и тех же единиц исключено, средняя ошибка выборки определяется следующим образом:
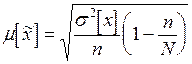 ,
,
Средняя ошибка выборки для признака 1:
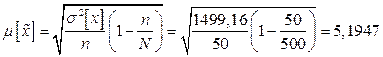
Величина выборки: n = 50 предприятий – 10%
Значит: N = 500 предприятий – 100%
Теория устанавливает соотношение между предельной и средней ошибкой выборки, гарантируемое с некоторой вероятностью:
 , где
, где
∆ - предельная ошибка выборки
µ - средняя ошибка выборки
t - коэффициент доверия.
При этом, коэффициент доверия определяется в зависимости от того, с какой достоверной вероятностью надо гарантировать результаты выборочного исследования. Для определения коэффициента доверия пользуются готовыми таблицами. Некоторые наиболее часто встречающиеся значения этого коэффициента приведены ниже:
| Доверительная вероятность | Коэффициент доверия |
| 0,683 | |
| 0,954 | |
| 0,990 | 2,5 |
| 0,997 |
Предельная ошибка выборки для признак-фактора
∆ = 5,1947* 2 = 10,3894
Таким образом, границы доверительного интервала признак фактора могут быть представлены как:
 то есть
то есть  ;
;
Границы доверительного интервала признак-фактора могут быть определены:
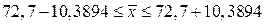 ;
;
или 62,3106 < x < 83,0894
Чтобы снизить предельную ошибку средней величины на 50% (в 2 раза) необходимо, чтобы предельная ошибка выборки (∆) уменьшилась в два раза, поэтому необходимая численность выборки составит:
 .
.
 предприятий
предприятий
Следовательно, для того, чтобы снизить предельную ошибку средней величины на 50%, необходимая численность выборки должна составлять 500 предприятий.
Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются средней ошибкой выборки, которая представляет собой среднее квадратическое отклонение возможных значений выборочных характеристик (оценок) от генеральных. Она определяется в зависимости от метода обора.
Доля альтернативного признака в выборочной совокупности определяется по формуле:
р = m / n,где
m – число элементов совокупности, которые больше моды
n – объем выборочной совокупности
р = 31 / 50 = 0,62
При повторном отборе, когда каждая отобранная и обследованная единица возвращается в генеральную совокупность, где ей опять предоставляется возможность попасть в выборку, средняя ошибка выборки определяется следующим образом:

Теория устанавливает соотношения между предельной и средней ошибкой выборки, гарантируемая с некоторой вероятностью. Выберем доверительную вероятность 0,954. Значит, коэффициент доверия равен 2.
∆ = µ * t, где
∆ - предельная ошибка выборки
µ - средняя ошибка выборки
t - коэффициент доверия.
∆ =0,066 *2= 0,132
Определим пределы, за которые не выйдет значение доли регионов, у которых объем промышленной продукции выше моды:
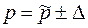 то есть
то есть 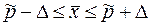
 .
.
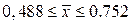 .
.
При повторном отборе необходимая численность выборки:
 (1)
(1)
Считая w маломеняющейся при изменении выборки, имеем:
 (2)
(2)
Разделив (1) на (2) имеем:
n = 50/0,64=79 предприятий..
При повторном отборе необходимая численность выборки должна составлять 79 предприятий.