Экономическая интерпретация параметров модели

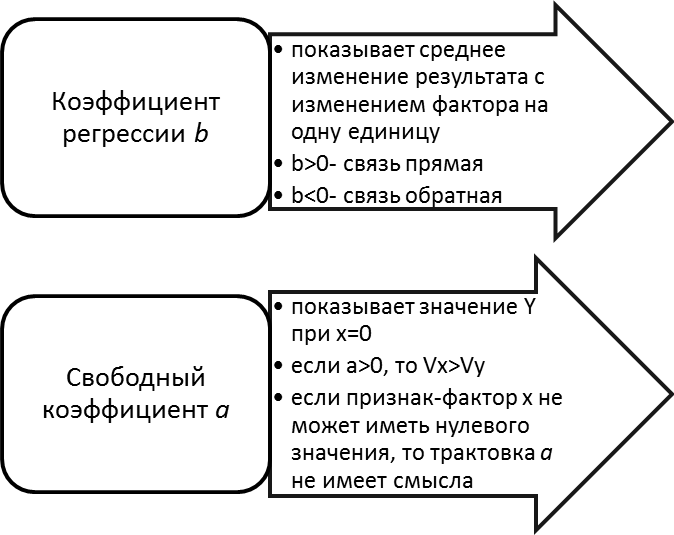
Рис. 4.1. Интерпретация параметров модели

Коэффициенты корреляции и детерминации в линейной модели парной регрессии. Если все точки лежат на построенной прямой, то регрессия Y на Х «идеально» объясняет поведение зависимой переменной. Обычно поведение Y лишь частично объясняется влиянием переменной Х.

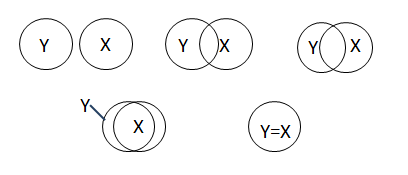
Рис. 4.2. Диаграмма Венна

Линейный коэффициент парной корреляции:

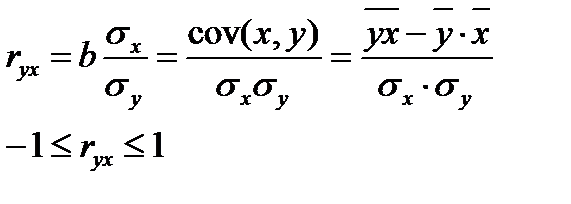
Если b>0, то r_yx>0; если b<0, то r_yx<0.

По абсолютной величине, чем ближе значение r_xy к единице, тем теснее связь, чем ближе значение r_xy к нулю, тем слабее связь между y и x.

Суммы квадратов отклонений:

- общая (TSS):

- регрессионная (ESS):

- остаточная (RSS):

Рис. 4.3. Геометрическая интерпретация

Выборочные оценки дисперсий:

- общая дисперсия:

- регрессионная дисперсия:

- остаточная дисперсия:

Коэффициент детерминации:

Коэффициент детерминации определяет долю разброса зависимой переменной Y, объясняемую регрессией Y на X.

Проверка качества модели линейной парной регрессии (верификация модели)

Рис. 4.4. Этапы проверки качества модели

1 этап:F-тест состоит в проверке гипотезы H₀ о статистической незначимости уравнения регрессии и показателя тесноты связи.

2 этап: T-тест состоит в проверке гипотезы Н₀ о статистической незначимости коэффициентов регрессии и корреляции.

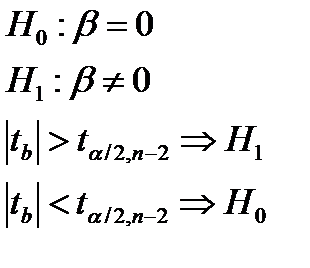
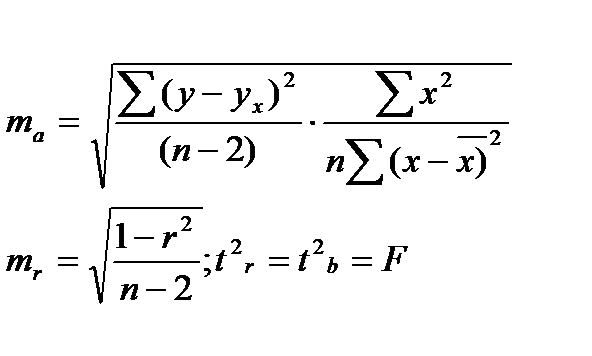
3 этап: проведение тестов на гетероскедастичность и автокорреляцию остатков.

Доверительные интервалы для коэффициентов теоретического уравнения регрессии:

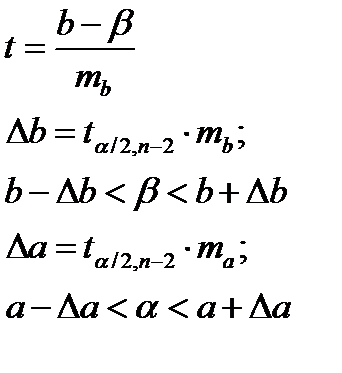
Интервалы прогноза по линейному уравнению регрессии. Предсказание среднего и индивидуального значения зависимой переменной:

где m_Yxp – стандартная ошибка точечного прогноза;

S² – остаточная дисперсия на одну степень свободы;

t – случайная величина, имеющая распределение Стьюдента с заданной вероятностью.

Вопросы и задания для самоконтроля

1. Каков экономический смысл коэффициента регрессии?

2. Какой смысл может иметь свободный коэффициент уравнения регрессии?

3. Какова связь между линейным коэффициентом корреляции и коэффициентом регрессии в линейной модели парной регрессии?

4. Каков статистический смысл коэффициента детерминации?

5. Как записывается баланс для сумм квадратов отклонений результативного признака?

6. Что происходит, когда общая СКО равна остаточной? В каком случае общая СКО равна факторной?

7. Что такое число степеней свободы? Чему равны числа степеней свободы для различных СКО в парной регрессии?

8. Как используется F-статистика в регрессионном анализе?

9. Как F-статистика связана с коэффициентом детерминации в парной регрессии?

10. Как рассчитать критерий Стьюдента для коэффициента регрессии в линейной модели парной регрессии?

11. В чем суть предсказания индивидуальных значений зависимой переменной?

Задача 1. Пусть имеется следующая модель парной регрессии, построенная по 20 наблюдениям: 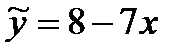. При этом 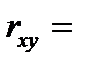- 0,5.

Задание: построить доверительный интервал для коэффициента регрессии в этой модели с вероятностями 0,9 и 0,95.

Задача 2. Анализируется зависимость между доходами горожан (X), имеющими индивидуальные домовладения, и рыночной стоимостью их домов (Y). По случайной выборке из 120 горожан данной категории получены результаты:

27343; 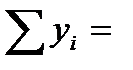115870; 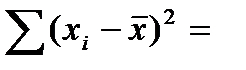75200;

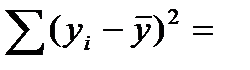1620340; 250431.

Задание: найти оценку коэффициента регрессии 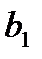и построить 95% доверительный интервал для коэффициента регрессии.

Лекция 6