Расчет скорости передачи данных

11.3.1 Скорость передачи данных по цифровому (дискретному) каналу имеет два определения: техническая скорость и скорость передачи информации.

Технической скоростью передачи или скоростью манипуляции называется число символов – элементарных сигналов, которые передаются за единицу времени – секунду. Она зависит от выбранных технических характеристик канала: быстродействия аппаратуры, вида и параметров направляющей среды.

Единицей измерения технической скорости служит «бод». Один бод соответствует скорости передачи одного символа – элементарного сигнала, за одну секунду , При передаче один элементарный сигнал представляет один определенный символ из множества возможных символов, которое получило название «алфавит символов». Например, при передаче по цифровому каналу элементарного сигнала – прямоугольного импульса , длительностью , который представляет символ – «лог.1», или при передаче символа «лог.0» прямоугольным импульсом 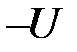длительности , техническая скорость передачи будет равна 1000 бод. Заметим, что роль символа «лог.0» может играть и отсутствие сигнала () на интервале .

С учетом возможных различий в длительностях передаваемых символов алфавита техническая скорость передачи определяется выражением 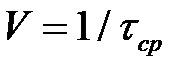, где – средняя статистическая длительность передаваемого символа. Например, при разной длительности элементов кодов букв (точек и тире) в азбуке Морзе, техническая скорость передачи данных (закодированных речевых сообщений) определяется величиной 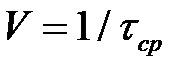. При случайном сочетании символов различной длительности, как в случае передачи речи символами азбуки Морзе, – определяется статистически, как математическое ожидание – среднее значение длительности символов, содержащихся в репрезентативных выборках.

Скоростью передачи информации называется среднее количество информации, которое передается по каналу в единицу времени. Она зависит от многих факторов:

– от технической скорости передачи (бод);

– от количества () возможных передаваемых символов – объема алфавита символов X, например, в двоичном канале цифровой передачи данных при объеме алфавита символов X;

– от вероятностей и статистической взаимосвязи, поступающих на вход канала символов алфавита X;

– от статистических свойств помех действующих в канале, которые приводят к тому, что переданный символ будет воспринят на выходе канала как 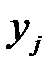, принадлежащий алфавиту выходных символов .

11.3.2 Получение информации человеком всегда связано с устранением некоторой степени априорной (до сеанса связи) неопределенности относительно случайного состояния наблюдаемого объекта (источника информации).

Получение информации – это результат устранения априорной неопределенности вследствие приема конкретного первичного сигнала, который является отражением конкретного состояния этого объекта из множества возможных, случайных для наблюдателя состояний.

Непременным условием количественной оценки информации является знание или практически оправданные предположения о статистических характеристиках возможных состояний источника, а, следовательно, и об ансамбле первичных сигналов источника информации. Без такого знания или оправданных предположений, ни о каком количестве получаемой информации (в статистическом понимании) речи идти не может.

Если источник априори с одинаковой вероятностью может находиться в одном из возможных состояний и каждому 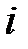– му его состоянию соответствует определенный первичный сигнал 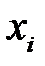, то количественную оценку неопределенности конкретного 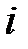– го состояния можно было бы дать, определив величину этой вероятности как . Однако при 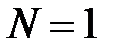состояние источника известно, выбора нет, но оценка вероятности существует, она равна . Следовательно, определнное количество информация будет получено, если будет принят сигнал о состоянии такого источника.

Однако в такой ситуации неопределенность отсутствует, т.е. априори известно в каком состоянии находится источник, и принятый сигнал никакой информации не несёт. Его получение не снимает никакой неопределенности, следовательно, количество информации должно быть равным нулю.

Кроме того вероятность, как мера, которая должна позволить количественно оценить неопределенность состояний источников информации, не аддитивна т.е. увеличение общего количества информации не может быть получено путем простого суммирования ее частных оценок. Например, если объединить два источника с равновероятными состояниями и , то число возможных состояний такого объединенного источника будет равно . Вероятность конкретного состояния этого источника , что противоречит интуитивному представлению об увеличении неопределенности.

11.3.3 Эти противоречия удалось преодолеть американскому ученому Р. Хартли (1928г.), который предложил в качестве меры неопределенности состояний источника с равновозможными состояниями логарифм вероятности его конкретного состояния 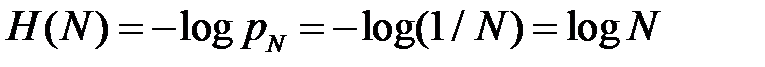. Знак «‒» принят для удобства, с тем, чтобы была положительной величиной, поскольку вероятность всегда меньше единицы () и ее логарифм – число отрицательное.

Основание логарифма не имеет принципиального значения и определяет только масштаб измерения величины неопределенности, т.е. единицу измерения. Например, , где . Логарифмические единицы, наиболее употребляемые в технике, получили следующие названия:

‒ бит – ;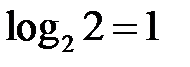

– дит – ;

– нет – .

В большинстве случаев возможные состояния источников информации не равновероятны, и в таких случаях пользоваться мерой Хартли невозможно.

Это препятствие преодолел американский ученый К. Шеннон (1946г.), который предложил усреднить количество неопределенности состояний источника с учетом вероятности каждого -го состояния 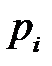. По аналогии с понятием энтропии (меры неопределенности) состояния замкнутой системы в физике, назвал предложенную меру энтропией дискретного источника информации.

Формула Шеннона имеет вид , где – положительное число, 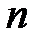– число возможных состояний источника.

В дальнейшем, принимая во внимание широкое распространение цифрового представления простейших сигналов, которые имеют только два возможных состояния 1 или 0, основание логарифма в формуле Шеннона выбрано равным 2, величина , а величина энтропии источника сообщения вычисляется по формуле

[бит].

В случае, когда 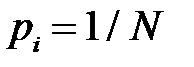получим оценку Хартли [бит].

Для практического применения энтропийных оценок количества информации полезно рассмотреть свойства энтропии:

1. Энтропия – величина вещественная и неотрицательная.

2. Частная оценка энтропии – го состояния источника пр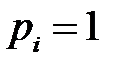и или 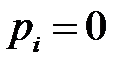равна нулю, поскольку и. , где .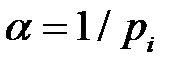

3. Энтропия максимальна, когда все состояния источника равновероятны.

4. Если вероятность хотя бы одного состояния источника 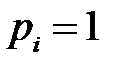, то .

5. Энтропия источника с двумя любыми возможными состояниями и 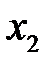принимает значения в интервале от нуля до нуля, достигая максимума – единицы (1 бит), при 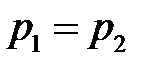, что характерно для битовых потоков на входе цифровых каналов связи при .

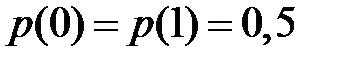6. Энтропия объединения нескольких статистически независимых источников информации равна сумме энтропий исходных источников. Например,

,

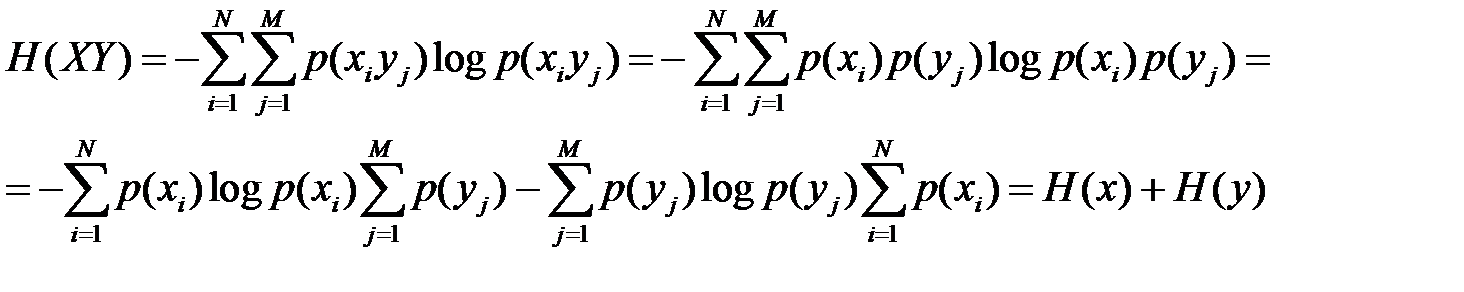поскольку выполняются условия, состоящие в том, что и .

7. Энтропия по Шеннону дает возможность количественно оценить только среднюю неопределенность любого одного состояния источника из ансамбля возможных случайных состояний. При этом содержательная сторона состояний источника полностью игнорируется. Например, энтропийная оценка неопределенности действия лекарства Л1, от которого 90% пациентов выздоравливают, а у 10% улучшается состояние не отличается от энтропийной оценки действия лекарства Л2, от которого 10% пациентов умерли, а у 90% состояние ухудшилось, поскольку и в тех и в других случаях средняя, в статистическом смысле, неопределенность результата одноразового применения лекарства одинакова

.

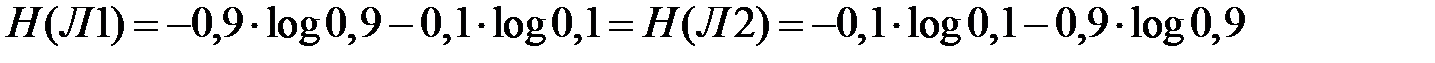8. Энтропийная оценка неопределенности согласуется не только с экспериментальными данными при исследовании технических систем, но и с результатами, полученными при изучении психологических реакций человека, в частности, реакций выбора действий в различных ситуациях и др.

11.3.4 Если канал передачи данных является идеальным, то любой сигнал на входе канала, представляющий то или иное состояние источника из алфавита X, будет принят на выходе канала без ошибки. Следовательно, при получении такого сигнала на выходе будет снята априорная неопределенность о соответствующем состоянии источника сообщений, т.е. получено некоторое количество информации, переносимой принятым сигналом.

В целом алфавит X объемом k переданных сигналов будет соответствовать алфавиту Y такого же объема k принятых сигналов. Если алфавит X имеет объем k=2 и содержит сигналы соответствующий «лог 0» и – соответствующий «лог 1», то канал передачи является двоичным цифровым.

В таком канале среднее количество информации, приходящееся на один сигнал (символ), которая вводится в канал на стороне источника, равно среднему количеству принятой, т.е. выполняется равенство

 

.

 

В реальных каналах передачи данных из-за искажений сигналов и помех некоторое количество информации теряется, поскольку имеет место неравенство . Например, в двоичном цифровом канале переданный символ «лог.1» может быть воспринят, как «лог.0» и наоборот.

В таком случае, среднее количество информации , передаваемое одним символом, определяется соотношением

(1)

Если статистические связи между символами, которые передаются по каналу, отсутствуют, т.е. они статистически не зависимы, то энтропия принятых символов алфавита на выходе (сигналов на выходе канала) описывается выражением

(2)

Если описать состояние канала (3) на выходе с учетом состояния на входе и при условии, что в канале из-за искажений сигналов и действия помех возникли ошибки, т.е. наблюдается частичная «трансформация» символов, например, в двоичном канале «лог.0» на входе воспринимается как «лог.1» на выходе и наоборот, и этот процесс характеризуется переходными вероятностями , например, , то апостериорная энтропия (послеопытная неопределенность в отношении действительного состояния источника сообщения) будет характеризовать уменьшение количества полученной информации.

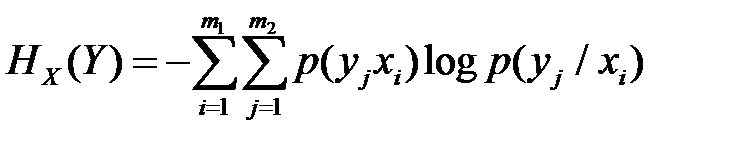(3)

Выразим через вероятности событий при передаче символов по каналу среднее количество информации , переносимое одним символом, подставив выражения (2) и (3) в (1)

 

. (4)

Если обеспечить техническую скорость передачи сигналов в канале максимально достижимой при его технических характеристиках и обеспечить максимальное значение среднего количества информации, передаваемой по каналу одним символом, то максимальная скорость передачи информации – пропускная способность дискретного канала с помехами, определится выражением

,

что возможно в том случае, когда вероятности поступления любых символов в канал одинаковы, а значит достигается максимум при любых возможных распределениях вероятностей входных сигналов. На практике к этому стремятся путем изменения статистических свойств последовательностей символов, поступающих на вход канала, посредством применения кодера канала. Однако, предельные возможности канала никогда не используются полностью. Степень его загрузки оценивается коэффициентом использования канала

,

где – производительность источника символов сообщений , равная энтропии символа, формируемого за единицу времени.

11.3.5 В случае двоичного симметричного канала имеем на выходе энтропию, приходящуюся на один символ сообщения, определяемую из выражения

= ).

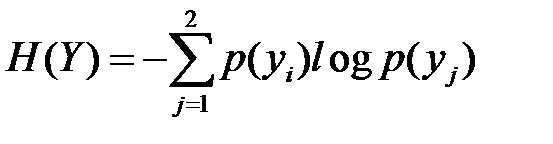При равенстве вероятностей появления символов достигается максимум

Информационная модель канала с искажениями и помехами представляет собой описание вероятностных свойств передачи символов со входа на выход. Если статистические характеристики канала изучены, то канал можно описывать матрицей условных вероятностей того, что принят символ 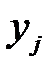при условии, что передавался символ 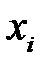. В реальных каналах эти вероятности зависят от многих факторов: характеристик сигналов – носителей символов; характеристик искажений и помех в канале; способов приема сигналов и принятия решений об обнаружении и распознавании символов.

Если матрица переходных вероятностей не изменяется во времени, то канал является стационарным без памяти, и, при одинаковом числе символов на входе и выходе равном k, его называют k -ичным. При k=2 канал – двоичный (Рис. 11.4).

Рисунок 11.4 – Схематическое представление символов на входе и выходе двоичного канала

и переходных вероятностей

 

Для стационарного дискретного двоичного (цифрового) канала без памяти матрица переходных вероятностей будет однозначно определяться четырьмя условными вероятностями

,

где и – вероятности передачи сигналов и правильного приема-обнаружения переданных символов; и – вероятности ошибочного приема-обнаружения или «трансформации» символов «лог.0» в «лог.1» и наоборот.

Запишем апостериорную энтропию (3) для двоичного канала в виде

При выполнении равенства вероятностей трансформации символов канал является двоичным симметричным, а в противном случае несимметричным. Существуют и другие модели каналов, однако именно двоичный симметричный исследовался наиболее интенсивно, и важнейшие результаты исследований были распространены на более широкие классы каналов.

Обозначим в симметричном стационарном цифровом канале условные вероятности ошибочного приема символов , и правильного приема – , поскольку .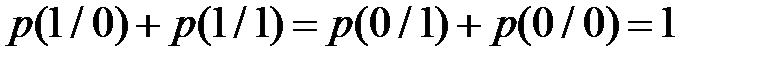

С учетом принятых обозначений условная энтропия равна

.

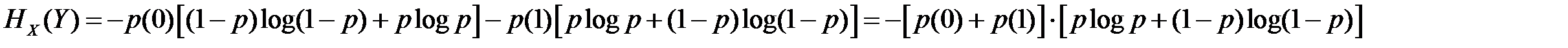Поскольку =1 условная энтропия не зависит от вероятностей символов на входе канала и .

.

Скорость передачи информации по каналу определяется как произведение технической скорости передачи на количество переданной информации

.

Пропускная способность канала 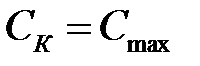наблюдается, когда 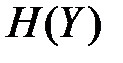принимает максимальное значение. В рассматриваемом случае согласно 5-му признаку энтропии при условии, что и описывается выражением

.

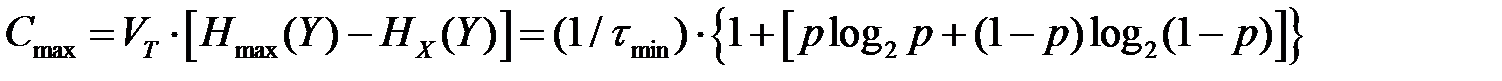При изменении условной вероятности ошибочного приема (вероятности трансформации символов 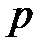) от 0 до 0,5 скорость передачи изменяется от 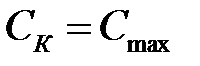до .

11.3.5 Расчет скорости передачи данных в реальном канале передачи рассмотрим на примере системы доступа, выполненной по технологии ADSL. Скорость передачи во многом определяются параметрами и характеристиками физического канала (линии передачи) от модема ADSL до мультиплексора доступа DSLAM. Рассмотрим связь между энергетическими параметрами таких линий и оценками качества их использования на примере расчета скорости передачи данных по выделенной линии ADSL.

В качестве показателя, по которому оценивается пропускная способность канала, часто принимается битовая скорость передачи данных. Если измеренная скорость передачи данных в линии близка к расчетному значению, то считается, что выбор параметров выделенной линии для предоставления доступа по технологии ADSL выполнен правильно. Если измеренная скорость передачи в линии по сравнению с расчетной не удовлетворяет выбранному критерию, есть возможность повторно выполнить расчеты, изменив исходные данные, и провести анализ причин, приводящих к потере скорости в данной линии.

В основе расчета потенциально возможного значения скорости передачи данных в линии лежит формула Шеннона, позволяющая рассчитать ее величину

,

где 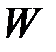– ширина используемой полосы частот [Гц], 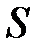– уровень сигнала, учитывающий затухание в линии [Вт], – уровень шума [Вт].

На основании теоремы Шеннона и с учетом требования стандарта G.992 получена формула для расчета скорости в линии ADSL в виде:

,

где – отношение сигнал/шум в i -м канале, число 20 – требуемый запас по помехозащищенности, указанный в стандарте G.992. При фиксированной мощности передатчика отношение SNR на стороне приема определяется затуханием сигнала и уровнем шума в линии.

11.3.2 График значений расчетного затухания в линии на витой паре категории 3, выполненной с использованием кабеля ТПП 0.5 длиной в 1 км, для различных частот сигнала приведен на рисунке 12.19. Для сравнения на этом графике указаны значения погонного затухания для линии со сходными параметрами, размещенные в справочнике Брискера.

Из рассмотрения рисунка 11.5 следует, что совпадение достаточно хорошее.

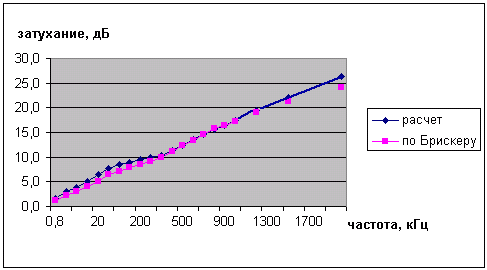
Рисунок 11.5 – График зависимости расчетного затухания кабеля ТПП 0,5 от частоты

11.3.3 Расчет уровня гауссового шума с равномерной спектральной плотностью в полосе частот пропускания кабеля выполнен с использованием международных стандартов масок спектральных плотностей белого шума ETSI/ANSI. На рисунке 11.6 приведены границы допусков ETSI/ANSI по затуханию для скорости 6 Мбит/с, которые соответствуют расчетной модели для кабеля ТПП 0,5 длиной 2,5 км. На оси частот графика зависимости затухания от частоты указаны пересчитанные значения частот парциальных каналов ADSL в соответствующие им номера каналов (бины).

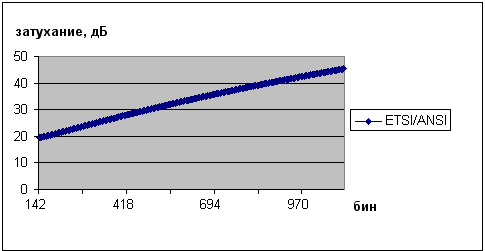
Рисунок 11.6 – Границы допусков ETSI/ANSI по затуханию для кабеля ТПП 0,5 длиной 2,5 км

Из рисунка 12.20 видно, что для обеспечения скорости передачи данных 6 Мбит/с для используемой модели затухания сигнала в линии ADSL с величиной запаса по помехозащищенности 20 требуемое отношение SNR может быть обеспечено при уровне спектральной плотности белого шума -110 дБм/Гц.

11.3.4 В настоящее время на рынке абонентских ADSL-модемов в основном предлагаются устройства, поддерживающие протокол ADSL2+ и скоростью передачи данных 24 Мбит/с. Модемы ADSL2+ совместимы и с более ранними стандартами, но следует учитывать, что технология ADSL2+ реализуется на кабелях с малым затуханием и длиной, как правило, до 2 км. На кабелях большей длины значения параметров протокола ADSL2+ модемами по умолчанию понижаются до значений сходных параметров протокола ADSL2, в котором каналы высокой частоты не используются.

На рисунке 11.7 приведена побиновая характеристика скорости передачи данных в канале ADSL2+ на кабеле ТПП 0,4 длиной 1 км (гистограмма 1), где заняты все каналы (бины), а также побиновая характеристика скорости передачи (гистограмма 2) при длине такого-же кабеля 2,5 км, где передача информации к абоненту занимает полосу частот только до 168 канала (бина).

 

Рисунок 11.7 – Побиновые характеристики скорости передачи в линиях разной длины в системе ADSL2+