Движения частиц идеального газа

Саратовский государственный технический университет

 

 

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ

C_P/C_V ВОЗДУХА.

 

Методические указания

к выполнению лабораторной работы по физике

для студентов всех специальностей

всех форм обучения.

 

Электронное издание локального распространения

 

Саратов 2006

 

Все права на размножение и распространение в любой форме остаются за разработчиком.

Нелегальное копирование и использование данного продукта запрещено.

 

 

Составитель – Евсеева Лидия Алексеевна.

 

 

Под редакцией Зюрюкина Юрия Анатольевича.

 

 

Рецензент – Вахлюева Валентина Ивановна

 

 

410054, Саратов, ул. Политехническая 77,

Научно-техническая библиотека СГТУ,

тел. 52-63-81, 52-56-01

http: // lib.sstu.ru

 

Регистрационный

Номер 060541Э

 

 

© Саратовский государственный

технический университет 2006 г.

Цель работы: определение отношения молярной теплоемкости при постоянном давлении к молярной теплоемкости при постоянном объеме C_P/C_V воздуха.

 

Теоретические представления о тепловых процессах в газах,

Модель идеального газа

Воздух при давлениях близких к атмосферному можно рассматривать как идеальный газ. Идеальным газом называют такой газ, в котором собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда, между молекулами отсутствуют силы взаимодействия, столкновения молекул между собой и со стенками сосуда абсолютно упругие.

Состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением , объемом и температурой .Между этими параметрами существует определенная связь, называемая уравнением состояния.

Для идеального газа уравнение имеет вид:

(1)

Это уравнение Клапейрона-Менделеева. В уравнении (1) m –масса газа, - молярная масса (масса одного моля вещества), - количество вещества, R=8,31Дж/(моль*К)– газовая постоянная.

Если один из основных параметров состояния сохраняется постоянным, то такой процесс называется изопроцессом.

1.Изотермическим процессом называется процесс изменения давления и объёма данной массы газа при постоянной температуре. Изотермический процесс описывается уравнением Бойля – Мариотта

pV = const при Т = const. (2)

2.Изобарическим процессом называется процесс изменения объема данной массы газа в зависимости от температуры при постоянном давлении. Изобарический процесс подчиняется закону Гей-Люссака.

V = V₀aT при p = const, (3)

где α = 1/273; Т – абсолютная температура.

3.Изохорическим процессом называется процесс изменения давления данной массы газа при постоянном объеме. Давление в этом случае зависит от температуры по закону Шарля

 

 

p = p₀aTпри V = const. (4)

Теплоёмкость газов

 

Теплоемкостьюлюбого тела или определенного количества вещества, называется величина, равная количеству тепла, которое необходимо сообщить телу, чтобы нагреть его на один кельвин (1 K= 1⁰ C). Теплоёмкость тела измеряется в Дж/К. Каждое вещество, в том числе каждый газ, можно охарактеризовать удельной и молярной теплоёмкостью.

Удельной теплоёмкостью газа называется физическая величина, равная количеству тепла, которое нужно сообщить единице массы газа, чтобы повысить его температуру на один кельвин. Единицей удельной теплоёмкости является Дж/(кг×К).

Молярной теплоёмкостью газа С называется величина, равная количеству тепла, необходимого для нагрева одного моля газа на один кельвин. Измеряется молярная теплоёмкость в Дж/(моль×К).

Моль – единица количества вещества. За 1 моль принято количество вещества, содержащее столько же атомов, молекул, ионов и т. д., сколько атомов содержится в 0,012 кг изотопа углерода C ¹². Это число частиц, содержащееся в моле любого вещества, называется числом Авогадро и равно 6,022 ×10²³ моль ^-1.

Масса вещества, взятого в количестве одного моля, называется молярной массой и обозначается μ. В округленных числах молярная масса водорода равна 0,002 кг/моль, кислорода – 0,032 кг/моль и т. д.

Используя понятие молярной массы, можно установить связь между молярной и удельной теплоёмкостью:

(5)

Теплоемкость в общем случае является характеристикой, как тела, так и условий нагревания. Она приобретает определенные числовые значения, если фиксировать условия нагревания.

Наибольший интерес представляет теплоёмкость тех случаев, когда теплота передаётся газу при постоянном объёме и при постоянном давлении. В соответствие с этим вводят удельную и молярную теплоёмкость при постоянном объёме , и при постоянном давлении , .

Покажем, что > _, то есть получим уравнение Майера . Смысл этого уравнения заключается в том, что при изобарическом нагревании газа на один градус к газу должно быть подведено больше тепла, чем для такого же изохорического нагревания.

Рассмотрим изохорическое и изобарическое нагревание одного моля газа. Для одного моля газа уравнение состояния имеет вид:

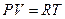(6)

При изохорическом нагревании газ не расширяется и, следовательно, не производится работы. Вся переданная газу теплота идет на увеличение внутренней энергии. Эту энергию обозначим через , она включает в себя кинетическую энергию теплового движения молекул идеального газа, а в реальном газе, кроме того, учитывается потенциальная энергия взаимодействия молекул друг с другом.

Из определения внутренней энергии следует, что она имеет вид вполне определенное значение в любом состоянии системы. Это означает, что внутренняя энергия является функцией состояния.

Величины , , , так же как и имеют вполне определенные значения в любом состоянии системы и характеризуют это состояние. Поэтому - являются полными дифференциалами.

Теплоемкость при постоянном объеме определяется как

 

(7)

Применим первое начало термодинамики в виде

 

(8)

к изохорическому процессу , тогда (8) имеет вид

(9)

Это означает, что при V=const – полный дифференциал. Тогда из (9) и (7) следует

(10)

При изобарическом нагревании газ расширяется и совершает работу

 

При P=const, (8) запишем в виде

 

(11)

Это означает, что - полный дифференциал и

(12)

Тогда из определения (12) и формулы (11) получаем

(13)

Так как уравнение состояния имеет вид (6),то

,

что при подстановке в (13) дает уравнение Майера

(14)

Число степеней свободы

движения частиц идеального газа

Для описания положения материальной точки в пространстве вводят понятие степеней свободы.

Числом степеней свободы движения механической системы называется число независимых координат, определяющих ее положение и конфигурацию в пространстве. Применяя это понятие к одноатомному идеальному газу нетрудно понять, что простая частица идеального газа имеет три степени свободы поступательного движения. Ее средняя кинетическая энергия равна 3кТ/2.

Многоатомные молекулы (сложные частицы) идеального газа, кроме поступательных, обладают еще вращательными и колебательными степенями свободы. В классической статистической физике доказывается теорема: если система находится в тепловом равновесии при температуре , то средняя кинетическая энергия равномерно распределяется между всеми степенями свободы и для каждой степени свободы молекул она равна кТ/2.

Таким образом, сложная частица обладает большим числом степеней свободы и, следовательно, большей энергией.

Рассмотрим простейший случай сложной частицы, состоящей из двух точечных частиц, между которыми возможны два типа связи. Первый тип – точечные частицы жестко связаны между собой и ведут себя наподобие жесткой гантели. В этом случае сложная частица имеет пять степеней свободы: три поступательные и две вращательные. Средняя кинетическая энергия такой частицы равна 5кТ/2.

Второй тип – связь между частицами не жесткая, и они могут совершать колебательные движения вдоль соединяющей их линии. В этом случае добавляется кинетическая энергия кТ/2 и потенциальная энергия кТ/2колебаний, то есть еще две степени свободы. Всего при этом на одну сложную частицу приходится энергия 7кТ/2. Аналогично можно рассмотреть энергию более сложных частиц. Если сложная частица имеет i степеней свободы, то ее энергия равна iкТ/2. В моле имеется частиц и, следовательно, внутренняя энергия моля идеального газа равна

(15)

где - число Авогадро, моль

Тогда по формуле (10) и (14) получаем

, (16)

Используя (16), можно найти выражение для показателя адиабаты

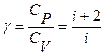(17)

Адиабатический процесс

В этом процессе газ остается теплоизолированным от внешней среды. Внутренняя энергия самого газа не остается постоянной, т. к. газ совершает работу при своем расширении (или при сжатии над ним совершается работа).

Общее уравнение адиабатического процесса получают из первого начала термодинамики, полагая в соответствии с условием теплоизолированности.

Тогда уравнение (8) имеет вид

(18)

Применим (18) к адиабатическому расширению газа. Подставляя (10) в (18) имеем

(19)

Разделив (19) на , найдем

(20)

где - показатель адиабаты, который в работе определяется для воздуха.

Интегрируя, а затем, потенцируя (20) получаем

 

(21)

Поскольку 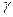> 1,то >0 и, следовательно, адиабатическое расширение сопровождается охлаждением, а сжатие – нагреванием.

Комбинируя выражение (21) с уравнением (6), получаем уравнение, связывающее давление с объемом

(22)

Уравнение (22) называют уравнением адиабаты.

Методика эксперимента

Экспериментальная установка состоит из большого стеклянного баллона 1, соединённого с манометром 2 и насосом.

рис.1

Кран 3 служит для прекращения выхода воздуха из баллона после накачивания. С помощью клапана с кнопкой 4 внутренний объём баллона может быть на короткое время соединён с атмосферой.

Для измерения давления в данной работе используют жидкостный манометр в виде - образной трубки, одно колено соединяется с сосудом, в котором нужно измерить давление, другое колено - открытое. Разность уровней жидкости в коленах называется разностью давления в сосуде и атмосферного давления вне его. Таким образом, давление в сосуде больше атмосферного давления на давление жидкости высотой в открытом колене манометра.

В манометре, используемом в установке, точность измерений ограничена использованием миллиметровой шкалы (ее основная инструментальная погрешность мм.), что обеспечивает незначительную абсолютную погрешность при измерении давления.

К систематическим погрешностям измерений следует отнести неточность шкалы, используемой в манометре.

В работе определение 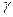производится классическим методом Клемана – Дезорма, основанным на исследовании некоторого объема воздуха, мысленно выделенного в баллоне.

Рассмотрим изменения, которые будет претерпевать в процессе опыта некоторый мысленно выделенный объём воздуха в баллоне. С помощью насоса накачаем в баллон некоторое добавочное количество воздуха. При накачивании воздух нагревается. Чтобы начать опыт, нужно подождать несколько минут, чтобы в результате теплообмена температура в баллоне сравнялась с температурой окружающей среды. При этом давление в баллоне несколько снизится.

Рассмотрение процесса начнём с того момента, когда температура и давление в баллоне установились.

1. Выделенная часть воздуха в баллоне в начале процесса будет характеризоваться параметрами (выше атмосферного), ,

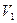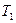
рис.2

 

(температура окружающей среды), что соответствует точке 1 на диаграмме pV (рис. 2).

2. Произведем адиабатическое расширение воздуха в баллоне. Для этого, нажав кнопку 4, соединим на короткое время внутренний объем баллона с атмосферой. Часть воздуха выйдет из баллона, а выделенный нами воздух расширится. Это расширение можно считать адиабатическим, так как оно происходит быстро и теплообмен с окружающей средой произойти не успевает.

На графике процесс расширения изображен отрезком адиабаты I-II. Давление в баллоне сравнивается с атмосферным, а температура понизится. Параметры выделенной части воздуха примут значение (атмосферное давление), , 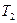(ниже температуры окружающей среды). Параметры воздуха в начале и в конце расширения связаны уравнением адиабаты (уравнение Пуассона):

(23)

3. После адиабатического расширения в течение 2-3 минут произойдет теплообмен между окружающей средой и воздухом в баллоне. Температура в баллоне поднимется до температуры окружающей среды, а давление повысится. Процесс изобразится отрезком изохоры II-III. Параметры газа примут значения P₃, V₂, T₁, (температура окружающей среды).

Сравнивая конечное состояние выделенной части воздуха III с исходным I, можно заметить, что они находятся при одной и той же температуре 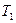. Такие состояния связаны уравнением изотермы (закон Бойля-Мариотта)

p₁ V₁ = p₃ V₂ (24)

 

Для определения показателя адиабаты возведем уравнение (24) в степень и разделим его почленно на уравнение (23).

или (25)

Выразим давление воздуха в баллоне через разность уровней жидкости в коленах манометра . Обозначим атмосферное давление буквой , а добавочное давление в состоянии I буквой и добавочное давление в состоянии III буквой . Тогда , и . В результате математических преобразований уравнения (25) получили:

(26)

 

Эта формула является рабочей формулой для определения показателя адиабаты g= C_p/C_v,