Основные понятия
Средняя величина – это обобщающая мера варьирующего признака, которая характеризует ее уровень в расчете на единицу совокупности. Условиями применения средних величин являются: наличие качественно однородной совокупности и достаточно большой её объем.
В статистической практике используют несколько видов средних: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратичная и т. д. Каждая из указанных средних может приобретать две формы: простую и взвешенную. Если средняя вычисляется по первичным (не сгруппированным) данным, применяется простая форма, если по вторичным (сгруппированным) – взвешенная.
Использование каждого вида средних зависит от двух обстоятельств, во-первых, от характера индивидуальных значений признака (прямые, обратные, квадратичные, относительные). Во-вторых, от характера алгебраической связи между индивидуальными значениями признака и общим объемом (сумма, произведение, степень, квадратичный корень). Эта связь является определяющим свойством совокупности и отражается в логической формуле усредняемого признака. На основании логической формулы выбирается вид средней.
Средняя арифметическая –используется для усреднения прямых значений признаков путем их суммирования. Ее логическая формула имеет вид
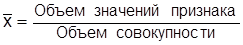 .
.
Если данные несгруппированные, используется средняя арифметическая простая
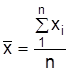 ,
,
где x i – отдельные значения признака,
n – объем совокупности.
Пример. Уставный фонд акционерной компании сформирован 6 учредителями; размер взноса каждого из них составляет, млн. грн.: 6; 10; 12; 9; 7; 4. Средний взнос одного учредителя
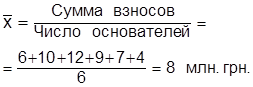
По формуле средней арифметической простой вычисляются также средние в хронологическом ряде, если интервалы времени, за которые даются значения признаков, одинаковые.
Пример. Квартальный оборот универсальных бирж в течение года составлял, млн. грн.: І кв. – 372; II кв. – 423; III кв. – 340; IV кв. – 455. Среднеквартальный оборот бирж составляет

Если в хронологическому ряду приведены моментные показатели, то для вычисления средней они заменяются полусуммами значений на начало и конец периода. Если моментов больше двух и интервалы между ними одинаковые, то средняя вычисляется по формуле средней хронологической
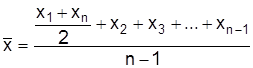 ,
,
где n –число моментов.
Пример. В коммерческом банке сумма кредиторской задолженности на начало каждого квартала составляла, млн. грн.: 01.01 – 20; 01.04 – 26; 01.07 – 32; 01.10 – 29; 01.01 следующего года – 22. Среднеквартальная сумма кредиторской задолженности
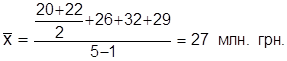
Если данные сгруппированы, то используют средневзвешенную арифметическую
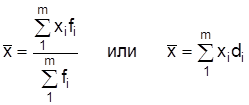 ,
,
где fi – частота;
di – частость i-й группы (удельный вес).
При этом 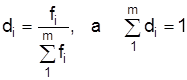 .
.
Так, по результатам сдачи экзамена студентами группы (табл. 4.1), средний балл оценок составляет 3,8.
Таблица 4.1
| Оценка знаний студентов, баллов | xi | Всего | ||||
| Количество оценок | fi | |||||
| Удельный вес оценок, % | di | 26,7 | 40,0 | 20,0 | 13,3 |
На основании частот
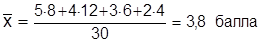 ,
,
на основании частостей
 .
.
Усреднению подлежат не только отдельные значения вариант, но и их групповые средние 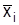 , тогда весом будет частота (частость) каждой группы:
, тогда весом будет частота (частость) каждой группы:
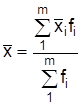 .
.
Вычисленная таким способом средняя из групповых средних называется общей.
Весом может быть также абсолютная величина, которая логично связана с усредняемым показателем. Выбор весов основывается на логической формуле показателя. Поскольку средняя величина вычисляется в расчете на единицу совокупности, то вес всегда будет находиться в знаменателе логической формулы. Например, при определении средней суммы расходов на одно рекламное сообщение весом будет количество рекламных сообщений. При вычислении средней суммы расходов на одного рекламодателя весом будет количество рекламодателей.
Средняя арифметическая имеет определенные математические свойства, которые раскрывают ее суть. Так, сумма отклонений отдельных вариант от средней равна нулю, а сумма квадратов таких отклонений приближается к минимуму. Эти два свойства положены в основу изучения вариации признаков.
Если отдельные значения вариант увеличить (уменьшить) на величину А или в kраз, то средняя изменится соответственно.
Например, если денежные взносы граждан в Сбербанк откорректировать на уровень инфляции, что составляет 1,2, то средний размер взноса увеличится соответственно в 1,2 раза. Средняя не изменится при пропорциональном изменении всех весов, но ее размер претерпевает изменения при определенных структурных сдвигах.
Например, при неизменной курсовой стоимости акций отдельных эмитентов средняя стоимость акций может повыситься за счет увеличения доли "дорогих" акций в общем количестве их продаж. Отмеченные свойства средней используют в случае усреднения признаков порядковой (ранговой) шкалы. Варианты признака можно оцифровать порядковыми рангами Ri = 1, 2,..., n или центрированными R0 = -2, -1, 0, 1, 2 (табл. 4.2). Очевидно, что 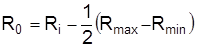 . Средний центрируемый бал отклоняется от среднего порядкового на величину
. Средний центрируемый бал отклоняется от среднего порядкового на величину  .
.
Средний центрируемый балл приобретает положительные или отрицательные значения и свидетельствует о позитивной или негативной оценке явления. Кроме того, его используют для сравнения оценок различных явлений, поскольку он не зависит от размерности шкалы. Поприведенными в табл. 4.2 данным об отношении населения к приватизации земли,
 ;
; 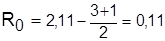 .
.
Следовательно, уровень поддержки приватизации земли позитивный, но пока что невысокий.
Таблица 4.2
| Отношение к приватизации | Частота ответов, % | Ранги | |
| Ri | R0 | ||
| Полностью поддерживаю | |||
| Частично поддерживаю | |||
| Не поддерживаю | - 1 | ||
| Всего | - | - |
Средняя гармоническая используется для усреднения обратных индивидуальных значений признаков путем их суммирования. Для несгруппированных данных это средняя гармоническая простая
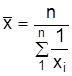 .
.
Если данные сгруппированы, то используют среднюю гармоническую взвешенную
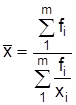 .
.
Очевидно, что среднюю гармоническую взвешенную целесообразно использовать, когда отсутствует информация о значении знаменателя логической формулы, т.е. отсутствуют веса.
Пример. Окупаемость расходов на развитие новаторских работ характеризуется данными табл. 4.3.
Таблица 4.3
| Новаторские работы | Доход от использования, млн. грн. | Окупаемость 1 млн. расходов на развитие новаторства, млн. грн. |
| Изобретения | 4,6 | |
| Рационализаторские предложения | 6,5 | |
| Всего | -- |
Логическая формула окупаемости расходов на развитие новаторства будет иметь вид
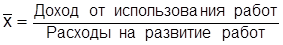 .
.
Поскольку в роли веса fi выступают расходы на развитие работ, которые в таблице отсутствуют, то применяется средняя гармоническая
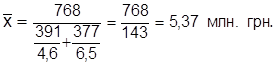
Рассчитывать среднюю можно и в том случае, когда отдельные значения вариантов не указаны, а известны только итоги (суммарные значения числителя и знаменателя) логической формулы.
Пример. Общий размер капитала пяти самых влиятельных коммерческих банков составлял 318,8 млн. грн., а общая сумма прибыли – 51,7 млн. грн. Средняя прибыльность капитала будет определяться по логической формуле
 .
.
Отсюда 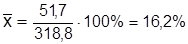 .
.
Средняя геометрическая определяется как произведение относительных величин динамики xi, которые являются кратными соотношению i-го значения показателя к предыдущему (i –1). Формула средней геометрической простой
 ,
,
где 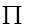 – символ произведения;
– символ произведения;
n – число усредняемых величин.
Пример. Количество зарегистрированных преступлений за четыре года выросло в 1,57 раза, в том числе за первый год – в 1,08, за второй – в 1,1, за третий – в 1,18, за четвертый – в 1,12 раза. Среднегодовой темп роста количества зарегистрированных преступлений составляет
 ,
,
т.е. число зарегистрированных преступлений росло ежегодно в среднем на 12%.
Если часовые интервалы неодинаковые, используют среднюю геометрическую взвешенную
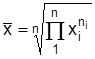 ,
,
где 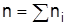 – часовой интервал.
– часовой интервал.
Средняя квадратичная рассматривается как характеристика вариации (тема 5).
Социально-экономические явления чрезвычайно сложные и многогранные. Любой показатель отражает только одну грань предмета познания. Комплексная характеристика последнего предусматривает использование системы показателей. Каждый показатель системы имеет самостоятельный смысл и в то же время является составляющей обобщающего свойства, которая дает основания для конструирования интегральных оценок явлений. Поскольку показатели системы, как правило, разноименные, то объединение их в интегральную оценку предусматривает стандартизацию – приведение к одному виду. При стандартизации индивидуальные значения показателей заменяются рангами, баллами, относительными величинами, стандартными отклонениями и тому подобное.
Так, рейтинговая оценка финансового состояния банков интегрирует пять параметров деятельности: качество капитала, качество активов, банковский менеджмент, прибыльность, ликвидность. Каждый параметр оценивается баллами – от 1 (сильный) до 5 (неудовлетворительный). Средний невзвешенный балл выступает как рейтинговая оценка финансового состояния банка. Если оценка качества капитала 3 балла, активов – 4, менеджмента – 3, прибыльности – 2 и ликвидности – 3, то средний балл составляет 15:5=3, т.е. финансовое состояние банка посредственное.
При стандартизации при помощи относительных величин базой сравнения может быть или эталонное значение (норма, стандарт) или среднее значение показателя по совокупности:
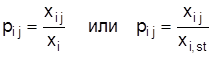 ,
,
где xi j – значение і-го показателя j-го элемента совокупности;
xi, st – эталонное значение этого показателя;
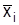 – среднее.
– среднее.
Среди показателей системы выделяются стимуляторы и дестимуляторы. Показатели-стимуляторы свидетельствуют о высоком уровне i-го показателя при pi j > 1; дестимуляторы – при pi j < 1. Чтобы привести их к однозначной характеристике, для дестимуляторов pi jвычисляется как обратная величина.
Средняя величина относительных m признаков, т.е. многомерная средняя, является интегральной оценкой j–го элемента совокупности:
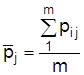 .
.
Если показатели системы считаются неравновесными, каждому из них присваивается определенный вес di, а расчет многомерной средней ведется по формуле арифметической взвешенной:
 .
.
При  уровень явления j-го элемента выше среднего в совокупности или нормативного; при
уровень явления j-го элемента выше среднего в совокупности или нормативного; при  , наоборот, ниже.
, наоборот, ниже.
В табл. 4.4 приведен расчет многомерной средней для оценки инвестиционной привлекательности j-го предприятия-эмитента. Показатели считаются равновесными, первые два – стимуляторы, третий и четвертый – дестимуляторы.
Многомерная средняя составляет 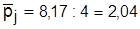 , т.е. финансовое состояние эмитента можно считать привлекательным для инвесторов.
, т.е. финансовое состояние эмитента можно считать привлекательным для инвесторов.
Таблица 4.4
| Показатель | Уровень показателя xi j | Норматив xi, st | Pi j |
| Рентабельность активов, % | 47,20 | 20,00 | 2,36 |
| Оборотность активов, | 0,80 | 0,67 | 1,19 |
| Коэффициент капитализации, % | 3,90 | <10,0 | 2,56 |
| Коэффициент задолженности | 0,34 | 0,70 | 2,06 |
| Всего | -- | -- | 8,17 |