Определение. Критической точкой (по второй производной) называется точка, в которой вторая производная равна нулю или не существует.
Теорема. Только критические точки могут являться точками перегиба. Не любая критическая точка является точкой перегиба.
Пример 47.1. Рассмотрим функцию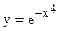 
. Легко проверить, что 
, 
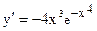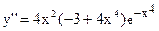. Вторая производная обращается в ноль при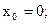 
; 
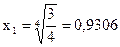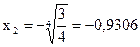. Соответствующие ординаты этих точек равны: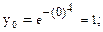 
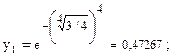
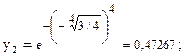Это критические точки (по второй производной). Знаки второй производной и график функции указаны на следующих рисунках:
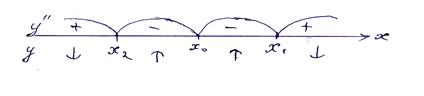Рис. 47.1.
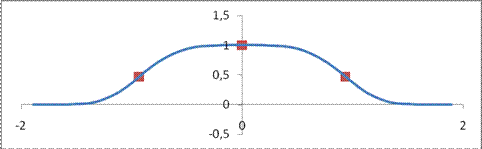
Рис. 47.2.
Хотя здесь три критические точки (по второй производной), но из рисунка видим, что точками перегиба являются только точки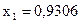 
и 
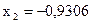. Точка 
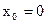не является точкой перегиба, но является точкой максимума.
Достаточные условия точки перегиба
Теорема. Если при переходе через точку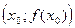 
вторая производная меняет знак, то эта точка является точкой перегиба.
Пример 48.1. Рассмотрим функцию 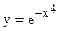из примера 47.1. Т.к. левее точки 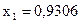вторая производна 
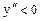, а правее 
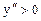(см. рис. 47.1), то точка 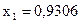является точкой перегиба. Аналогичные рассуждения можно провести для критических (по второй производной) точек 
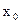и 
.
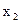Асимптоты
Определение. Прямая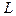 
называется асимптотой графика функции 
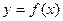, если расстояние от точки 
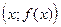, лежащей на графике, до прямой 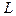стремится к нулю при удалении точки 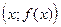в бесконечность.
Теорема. Прямая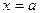 
является вертикальной асимптотой, если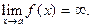 
Теорема. Прямая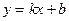 
является наклонной асимптотой, если существуют (конечные) пределы:
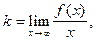
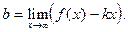
Пример 49.1. Из рис. 49.1 видно, что прямые у=0 (ось абсцисс) и х=0 (ось ординат) являются асимптотами функции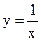 
.
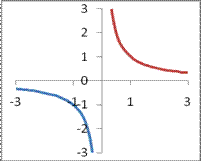
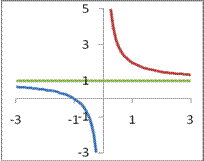
Пример 49.2. Если гиперболу 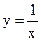поднять на одну единицу вверх, то получим (см. рис. 49.2) график функции 
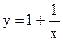. В этом случае асимптотами являются прямые х=0 и у=1.
Рис. 49.1. Рис. 49.2.
План построения графиков
Для построения графика рекомендуется определить:
1)область определения функции;
2)точки разрыва;
3)четность, нечетность функции;
4)периодичность функции:
5)точки пересечения с осями координат;
6)вертикальные асимптоты;
7)наклонные асимптоты;
8)определение экстремумов функции, интервалов возрастания и убывания функции;
9)определение точек перегиба и интервалов выпуклости.
Пример 50.1. Построим график функции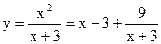 
(рис.50.3).
1)Функция определена для всех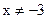 
.
2)При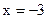 
функция терпит разрыв второго рода.
3)Функция не является четной и не является нечетной, т.к.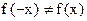 
и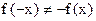 
.
4)Функция не является периодической.
5)Единственная точка пересечения с осями координат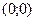 
.
6) Вертикальная асиптотоа 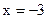, т.к. при 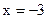функция равна бесконечности.
7)Найдем наклонную асимптоту: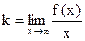 
= 
=
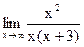=два раза правило Лопиталя=1,
= 
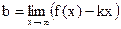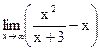=самостоятельно=-3.
Наклонная асимптота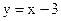 
.
8) 
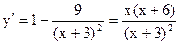. Критические точки: 
, 
, 
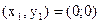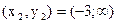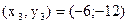. Знаки первой производной указаны на рис.50.1. Функция возрастает при 
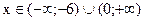. Убывает при 
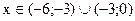(cм. рис. 50.3).
9) 
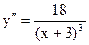. Одна критическая точка 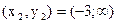. Знаки второй производной указаны на рис.50.2. Функция выпукла вверх при 
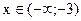. Выпукла вниз при 
.
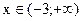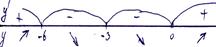
Рис. 50.1. Рис. 50.2.
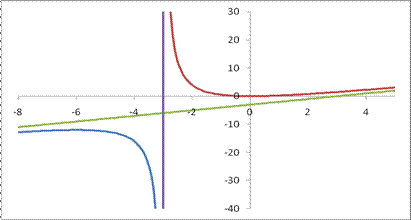
Рис. 50.3.
Пример 50.2. Построим график функции y=x-lnx.
1) Функция определена при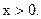 
2)Одна точка разрыва (второго рода) при х=0. На множестве (0;+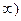 
функция непрерывна.
3)Не является ни четной, ни нечетной (т.к. неопределена при отрицательных х).
4)Функция не является периодической.
5) Т.к.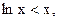 
то график не пересекается с осью 0Х. Т.к. при х=0 функция неопределена, то график не пересекается с осью ОУ.
6)Т.к.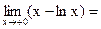 
0-(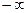
)=+ 
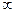, то х=0 – вертикальная асимптота (см. рис. 50.5).
7)Найдем наклонную асимптоту:
k=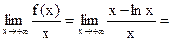 
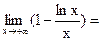
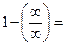
=правило Лопиталя=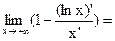 
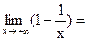1-0=1,
= 
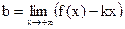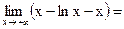
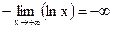, т.к. не существует (конечного) 
, то наклонной асимптоты нет.
8)Найдем производную: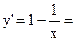 
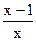. Определим критические точки: 
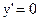при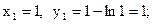 
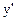не существует при 
.
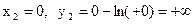Знаки первой производной на рис. 50.4. График функции на рис. 50.5.
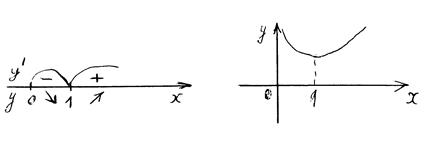
Рис. 50.4. Рис. 50.5.
9) Вторая производная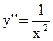 
>0 при x>0. Поэтому функция выпукла вниз. График, построенный на рис. 50.5 править (учитывая вторую производную) не нужно.
Кстати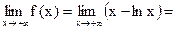 
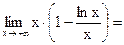
=Правило Лопиталя=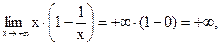 
что и отражено на рис. 50.5.
Пример 50.3. Построим график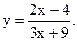 
1)Функция определена при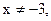 
2)При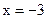 
функция имеет разрыв второго рода.
3)Функция не является ни четной, ни нечетной.
4)Функция не является периодической.
5)График пересекает ось 0Х при х=2, а ось 0У при у=-4/9.
6) Вертикальная асимптота х=-3.
7)Найдем наклонную асимптоту: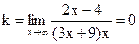 
, 
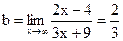. Прямая 
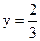является горизонтальной асимптотой.
8)Производная (убедитесь самостоятельно)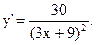 
Критическая точка только 
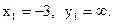Следовательно, экстремумов нет.
Знаки первой производной указаны на рис. 50.6, а график см. рис.50.7.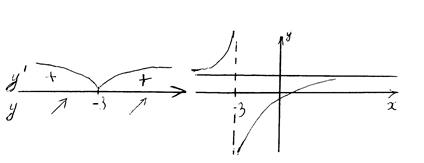 
Рис. 50.6. Рис. 50.7.
9)Вторая производная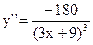 
положительна при х<-3 и отрицательна при x>-3, что и указано на рис. 50.7.
Пример 50.4. Приведем полное исследование функции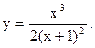 
1)Функция определена при всех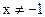 
.
2) 
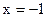- абсцисса точки разрыва.
3)Функция не является четной и не является нечетной.
4)Функция не является периодической.
5)График пересекает оси ОХ и ОУ при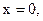 
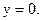
6)Вертикальная асимптота х=-1.
7) 
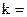
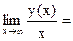
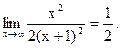
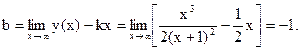Прямая 
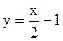является наклонной асимптотой.
8)Убедитесь, что производная: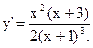 
. Критические точки: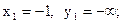 
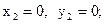
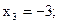
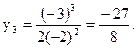Следующий рисунок показывает знаки первой производной и график функции. Точка с координатами 
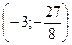является точкой максимума. 9)Убедитесь, что 
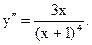Критические точки: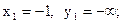 
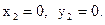Функция выпукла вверх, если 
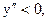т.е. при 
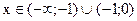. Функция выпукла вниз, если 
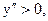т.е. при 
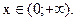Следовательно, точка 
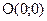является точкой перегиба.
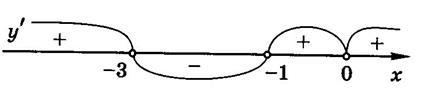
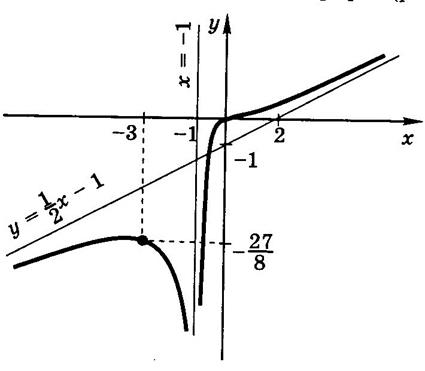
Рис. 50.8.