Определение производной
Определение. Пусть 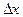 - некоторая величина, которую назовем приращением аргумента. Тогда
- некоторая величина, которую назовем приращением аргумента. Тогда 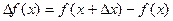 назовем приращением функции.
назовем приращением функции.
Определение. Производной от функции 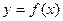 в точке х называется предел
в точке х называется предел 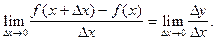
Производная обозначается 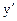 или
или 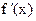 , или
, или 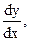 или
или 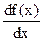 и т.д.
и т.д.
Определение. Если производная (существует и) конечна, то функция называется дифференцируемой.
Пример 17.1. Вычислим (пользуясь определением) производную функции 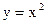 .
. 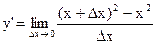 =Ш=
=Ш=  =
=
= 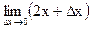 =
= 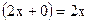 .
.
Геометрический смысл производной
Теорема. Производная от функции 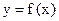 в точке
в точке 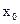 равна угловому коэффициенту касательной к кривой
равна угловому коэффициенту касательной к кривой 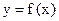 , проведенной в точке
, проведенной в точке 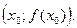 Уравнение касательной имеет вид:
Уравнение касательной имеет вид: 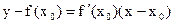 .
.
Пример 18.1. Найдем уравнение касательной к графику функции 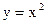 в точке
в точке 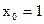 :
:
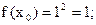
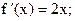
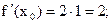 уравнение касательной
уравнение касательной 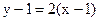 или
или 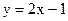 (см. рис. 18.1)
(см. рис. 18.1)
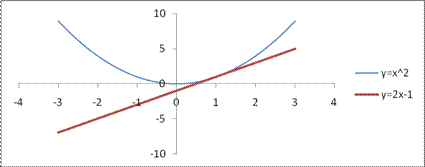
Рис. 18.1.
Производная от постоянной величины
Теорема. Производная от постоянной величины равна нулю. Т.е. 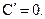
Пример 19.1. 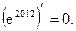
Производная от степенной функции
Теорема. Если 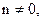 то
то 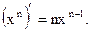
Пример 20.1. 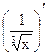 =Ш=
=Ш= 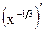 =
= 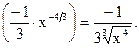
Производная суммы
Теорема. Если существуют (конечные) производные функций 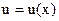 и
и 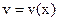 , то существует производная суммы (разности) этих функций и
, то существует производная суммы (разности) этих функций и 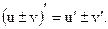
Пример 21.1. 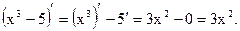
Пример 21.2. 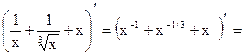 10 и 8=
10 и 8=
= 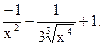
Производная от произведения функций
Теорема. Если существуют (конечные) производные 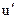 и
и 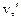 то существует производная от произведения этих функций и
то существует производная от произведения этих функций и 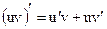 .
.
Пример 22.1. 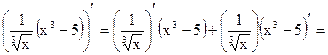
= § 20, § 21, Ш = 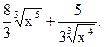
Производная частного
Теорема. Если существуют (конечные) производные 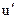 и
и 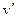 и
и  , то существует производная от частного этих функций и
, то существует производная от частного этих функций и 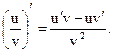
Пример23.1. 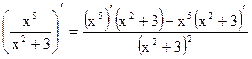 =
= 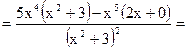 Ш=
Ш= 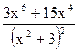
Производные от тригонометрических функций
Теорема. Справедливы следующие формулы: 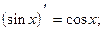
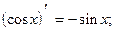
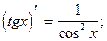
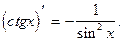
Пример 24.1. 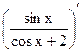 = §23 =
= §23 =
= 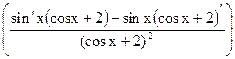 =
= 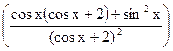 =
=
=Ш= 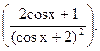
Производная сложной функции
Определение. Если 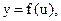 а
а 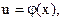 то
то 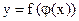 называется сложной функцией.
называется сложной функцией.
Замечание. Аргумент 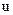 будем называть зависимым аргументом, а
будем называть зависимым аргументом, а 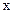 - независимым аргументом. Но в формуле
- независимым аргументом. Но в формуле 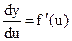 мы предполагаем, что производная определена, когда
мы предполагаем, что производная определена, когда 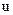 - независимый аргумент.
- независимый аргумент.
Теорема. Если существуют (конечные) производные 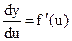 и
и 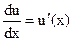 , то существует производная
, то существует производная 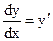 и
и 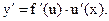
Пример 25.1. Если х независимый аргумент, то из §21 следует 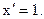 Аналогично
Аналогично 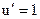 , если u является независимым аргументом. Формула
, если u является независимым аргументом. Формула 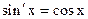 не всегда удобна, т.к. здесь нужно подразумевать, что х – независимый аргумент. Но если чуть поправить
не всегда удобна, т.к. здесь нужно подразумевать, что х – независимый аргумент. Но если чуть поправить 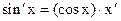 , то мы получим универсальную формулу. В литературе, как правило, она приводится в следующем виде
, то мы получим универсальную формулу. В литературе, как правило, она приводится в следующем виде 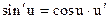 . Буквой х, как правило (но не всегда), обозначается независимый аргумент.
. Буквой х, как правило (но не всегда), обозначается независимый аргумент.
Пример 25.2. 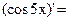 обозначим
обозначим 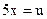 = =
= = 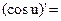
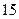 =
= 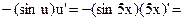 9 и 7=
9 и 7= 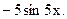
Производная от логарифмической функции
Теорема. 
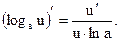
Пример 26.1.
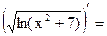 обозначим
обозначим 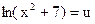 =
= 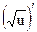 =13=
=13=
= 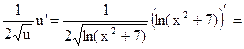
= обозначим 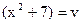 =
= 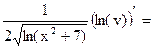 19=
19=
= 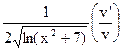 =
= 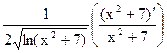 = 8 и 6 =
= 8 и 6 =
= 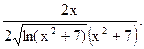
Производная от показательной функции
Теорема. 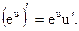
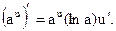
Пример 27.1. 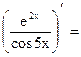 12=
12= 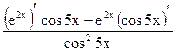 =
=
= 21 и 15 = = 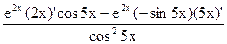 = 9 и 7 =
= 9 и 7 =
= 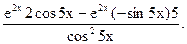
Производные от обратных тригонометрических функций
Теорема. 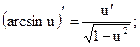
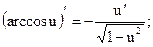
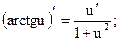
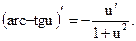
Пример 28.1.
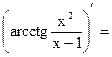 25, 12, 8=
25, 12, 8= 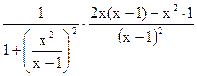 =Ш=
=Ш=
= 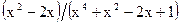 .
.
Дифференциал
Если функция 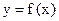 дифференцируема в точке х, т.е. имеет в этой точке конечную производную
дифференцируема в точке х, т.е. имеет в этой точке конечную производную 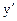 , то
, то 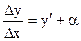 , где
, где 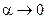 при
при 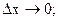 отсюда
отсюда 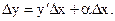
Определение. Главная часть 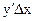 приращения
приращения  функции, линейная относительно
функции, линейная относительно 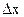 , называется дифференциалом функции и обозначается
, называется дифференциалом функции и обозначается 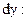
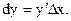
Теорема 29.1. Если х – независимый аргумент, то 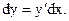
Теорема 29.2. Запись дифференциала 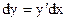 не зависит от того, является ли
не зависит от того, является ли 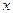 независимым аргументом, или функцией от другого аргумента. Это свойство называется инвариантностью первого дифференциала.
независимым аргументом, или функцией от другого аргумента. Это свойство называется инвариантностью первого дифференциала.
Пример 29.1. 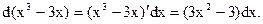
Пример 29.2. Если 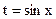 , то
, то 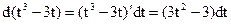 =
= 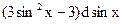 =
=
= 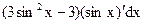 =
= 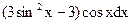 .
.
Свойства дифференциала функции
Теорема. 1. 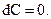 2.
2. 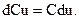 . 3.
. 3. 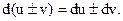 4.
4. 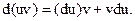 5.
5. 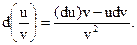 (Самостоятельно уточните формулировки этих формул).
(Самостоятельно уточните формулировки этих формул).