Содержание задачи.
Понтон плавает таким образом, что один из его торцов полностью выступает из воды, а другой – касается ее поверхности своей верхней кромкой (рис 1).
Определить объемное водоизмещение понтона и силы избыточного гидростатического давления на погруженный торец Rит и на подводную часть цилиндрической поверхности Rиц.
При определении искомых величин, принт, что понтон покоится на акватории без течений и ветра, т.е. решается гидростатическая задача.
2. Исходные данные и принятые положения:
Длинна понтона, L, м 44
Диаметр понтона, D, м 8
Положение понтона в воде см. рис.1
Плотность воды, ρ, т/м3 1,025
Ускорение свободного падения, g, м/сек2 9,81
В работе принята декартова система координат с началом на свободной поверхности (см. рис. 1). При этом оси X и Z лежат в продольно-вертикальной плоскости симметрии подводной части понтона (в диаметральной плоскости): ось X горизонтальна, а ось Z направлена вертикально. Ось Y перпендикулярна диаметральной плоскости (ДП).
Ось симметрии понтона обозначена как ось Х1, а перпендикуляр к ней в ДП – как ост Z1 (см. рис. 1).
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
| Лист |
| КР.ГМХ.260302.22 |
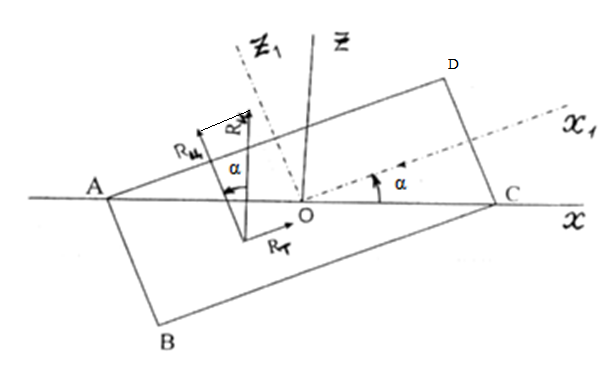
Рис. 1
Определение объемного водоизмещения V.
Объемное водоизмещение (объем подводной части) понтона V при описании в. п. 1 его посадке будет равно половине полного объема понтона Vп, т.е.
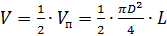 , (1.1)
, (1.1)
где: 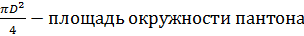
L – длина понтона
V = 0,5 · 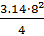 · 44 = 1105,28 (м3)
· 44 = 1105,28 (м3)
Определить силы избыточных давлений, действующей на всю смоченную поверхность понтона.
В соответствии с п.1 задача решается в условиях гидростатики.
В таком случае, как известно [1,с.13,(8)] результирующая сила от избыточных давлений Rи, действующая на подводную часть тела (в нашем случае понтона), равна по модулю произведению удельного веса воды γ на объемное водоизмещение V и направлена вертикально вверх по оси Оz (рис.1) и проходит через центр подводного объема понтона.
Rи = γ · V (1.2)
где: γ - удельный вес, равняющийся γ = ρ·g
V – объем тела
Rи = 1,025·9,81·1105,28 = 11,1·103 (кН)
Понтон в целом и его подводная часть, в частности, имеют продольно-вертикальную плоскость симметрии: диаметральную плоскость x1Oz1.
Следовательно, результирующая сила, от избыточных давлений Rи лежит в диаметральной плоскости (ДП).
5. Определение сил избыточного давления, действующих на погруженный торец 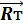 и на подводную часть цилиндрической поверхности понтона
и на подводную часть цилиндрической поверхности понтона 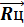 .
.
Ввиду симметрии понтона сила 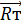 и
и 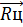 будут, как и результирующая сила
будут, как и результирующая сила 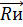 , лежать в диаметральной плоскости. При этом сила
, лежать в диаметральной плоскости. При этом сила 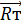 будет параллельна оси понтона Ox1, а сила
будет параллельна оси понтона Ox1, а сила 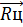 – перпендикулярна этой оси.
– перпендикулярна этой оси.
Эти силы можно представить как катеты треугольника с гипотенузой, равной результирующей силе 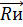 .
.
Так как один из катетов – сила Rц перпендикулярна оси понтона (оси Ox1), а гипотенуза – сила Rи перпендикулярна свободной поверхности водоема, (изображенной на рис.1 как ось Ox), угол ɑ между этими силами равен углу наклона оси понтона к поверхности воды, т.е. равен
ɑ = arctg  (1.3)
(1.3)
где:
D – диаметр понтона
L – его длина
ɑ = arctg 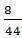 = 100
= 100
В соответствии с рис.1 силы-катеты Rт и Rц могут быть выражены через известную гипотенузу Rи и найденный угол ɑ по формулам:
Rт = Rи · sin ɑ = 11,1·103 sin 10 = 1,9 кН (1.4)
Rц = Rи · cos ɑ =11,1·103 cos 10 = 10.9 кН (1.5)
От
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
| Лист |
| КР.ГМХ.260302.22 |
Rт = 1,9 (кН)
Rц =10.9 (кН)