Табл. № 1
| Марка стали | Температ. отпуска 0С | Предел прочности sв, Н/мм2 | Предел текучести sт, Н/мм2 | Твердость НВ | Примечан. | |
| Стали с объемной закалкой | ||||||
Продолжение Табл. № 1
| Марка стали | Температ. отпуска 0С | Предел прочности sв, Н/мм2 | Предел текучести sт, Н/мм2 | Твердость НВ | Примечан. |
| 40X | |||||
| 30XГСА | |||||
| 40XНМА | |||||
| 12XНЗА | -- -- -- -- |
Табл. №2
| Марка стали. | |||
| шестерни | колеса | шестерни | колеса |
| 50Г | 35, 35Л, 40Л 40, и 45, 35Л | 35X, 40X 30XГСА 40X Н | 50, 55, 40Л 35X, 40X 35X, 40X |
Колеса ответственных передач в транспортных машинах, как правило, при Т2 > 200000 Н*мм, должны иметь твердость зубьев НВ1 = НВ2 > 350 и более вязкую сердцевину. Различная твердость в одном объеме металла получают, путем поверхностной закалки токами высокой частоты (ТВЦ) или химико – термической обработкой (цементация, азотирование и т.п.).
Наиболее производительна закалка ТВЧ по контуру зубъев колес из сталей с содержанием углерода 0,3…0,5%. Это стали 40Х, 35XM, 40XH. Толщина закаленного слоя при этом 3…4 мм и твердость поверхности 45…55 HRC.
Закалку ТВЧ по технологическим причинам применяют для обработки зубьев с модулем m ³ 5 мм. Мелкомодульные колеса изготавливают из малоуглеродистых сталей (0,12…0,3 % С) с последующей цементацией поверхностных слоев зубьев и закалкой. Глубина цементируемого слоя не превышает 2 мм, твердостью поверхности зубьев 50…60 НКС. Это стали 20X, 18XГТ, 12XHЗА и др.
Выбор термической или химико-термической обработки материалов колес может быть скорректирован после прочностного расчета и определения модуля зацепления. Некоторые рекомендуемые сочетания марок сталей для шестерни и колеса при НВ > 350 приведены в табл. 3.
Табл. № 3
| Марка стали. | |
| шестерни | колеса |
| 45, 50 55, 55Г 35X, 40Г 40XH 15X, 20X | 40, 50 50, 55 35X, 40X 15X, 20X |
В табл. 4 приведены механические свойства некоторых марок сталей, полученные поверхностным термическим и химико-термическим упрочнением. Причем НRС указывает на поверхностную твердость сталей, а σв, σТ и НВ - это характеристики сердцевины Табл. 4
| Марка стали | Предел прочности, Н/мм2 | Предел текучести, Н/мм2 | Твердость НВ | Твердость HRC | |||
| Стали с цементацией | |||||||
| 20X | 56-62 | ||||||
| 20ХГ | 56-62 | ||||||
| 18ХГТ | 56-63 | ||||||
| 12ХНЗА | 56-63 | ||||||
| 2оХГНМ | 56-63 | ||||||
| 20ХНМ | 56-63 | ||||||
| Стали с поверхностной закалкой ТВЧ | |||||||
| 40Х | 42-50 | ||||||
| 35ХМ | 50-56 | ||||||
| 40ХН | 50-56 | ||||||
Закалка колес после цементации приводит к короблению зубьев, поэтому необходимо дополнительные доводочные операции (шлифование, полировка, обкатка) Другие виды химико-термической обработки (азотирование, нитроцементирование и т.п.) в общем, машиностроение применяются редко.
Первоначально студенту трудно выбрать необходимое сочетание материалов шестерни и колеса, поэтому в табл. 5 приведены примерные рекомендации по выбору твердости материала шестерни в зависимости от передаваемого крутящего момента.
Табл. № 5
| Т2, Н. мм. | НВ1 | ∆HB |
| < 25000 | 250…280 | 30…50 |
| 25000 £ Т2 < 100000 | 280…320 | 30…50 |
| 10000 £ Т2 < 200000 | 320…350 | 30…50 |
| 200000 £ Т2 < 500000 | 350…450 | |
| Т2 ³ 500000 | 450…600 |
Примечание: При выборе НВ1 для цилиндрической передачи червячно – цилиндрического редуктора (первая ступень червячная, а вторая ступень цилиндрическая передача) есть особенность. Независимо от величины Т2 следует брать НВ1 = 250…300, т.к. существует опасность «налезания» колеса червячной передачи на вал колеса цилиндрической передачи.
Поясним вышеизложенное на примере:
Т2 = 470400 Н.мм. По табл. 5 требуемая твердость НВ1 = 350…450 по табл. 3 возможное сочетание материалов шестерня – сталь 40 XH, колесо – сталь 40X с поверхностной закалкой ТВЧ до НВ1 = НВ2 = 450 и ∆HB = 0 (Табл. 4).
Для тихоходных, преимущественно крупногабаритных и открытых зубчатых передач в качестве материала для зубчатых колес возможно применение чугуна различных марок.
В табл. 6 приведены механические свойства некоторых марок чугуна, применяемого для изготовления зубчатых колес.
Табл. 6
| Род | Марка | Предел прочности | Твердость | |
| чугуна | чугуна | при изгибе σвм | НВ | С1 |
| Н/мм2 | ||||
| Серый | СЧ16-32 | |||
| СЧЛ4-44 | 170...190 | |||
| Модифици- | СЧ32-О2 | 170... 241 | ||
| рованный | СЧЗо-56 | 197...248 |
Допускаемые контактные напряжения.
Допускаемые контактные напряжения при расчете зубчатых передач на контактную прочность определяются по формуле:
,
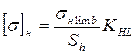где σh limb - базовый предел выносливости поверхностей зубьев по контактным напряжениям для пульсирующего (П-го) цикла, значения которого приведены в табл. 7
Табл. 7
| № | Термообработка или химико-термическое упрочнение | Твердость | σh limb, Н/мм2 |
| I. | Нормалиэапия или улучшение | HВ ≤ 350 | 2НВ+70 |
| 2. | Объемная закалка | НRС = 38...50 | I8HRC+150 + 150 |
| 3. | Поверхностная закалка | HRС = 40...56 | I7HRC+200 + 200 |
| 4. | Цементация | НВС = 54...64 | 23HRC |
| 5. | Азотирование | ККС = 55...75 | 20HRC |
Sн - коэффициент безопасности, который можно принять:
Sн = 1,1 - для случая нормализации, улучшения и объемной закалки;
Sн = 1,2 - для случая поверхностной закалки, цементации и азотирования;
КHL - коэффициент долговечности, зависящий от характера нагрузки и от числа циклов нагружения зубьев.
Коэффициент долговечности КHL определяется: при постоянной нагрузке
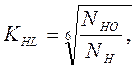
где Nно - базовое число циклов, при котором наступает предел выносливости. Для контактных напряжений Nно = 30·НВ^2,4 (HB -твердость материала по Бринеллю); Nн = 60·n·t - число циклов нагружения зубьев; n - частота вращения шестерни или колеса в об/мин; t - желательная длительность работы передачи в часах (при выполнении проекта можно принять t = 10000...20000 час); при переменной нагрузке подсчитывается некоторое эквивалентное число циклов нагружения зубьев по формуле:
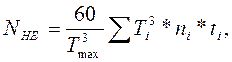
тогда
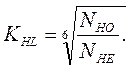
Обычно переменная нагрузка условно рассматривается как ступенчато-переменная, и циклограмма переменной нагрузки должна быть задана.
Приведем пример расчета эквивалентного числа циклов нагружения для переменной нагрузки, меняющейся но циклограмме. В этом случае:
= 
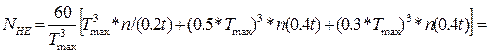
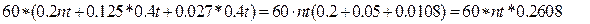
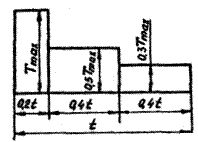
где T1 = Tmax; T2 = 0.5·Tmax; T3 = 0.3·Tmax;
t1 = 0.2t; t2 = 0.4t; t3 = 0.4t;
n1 = n2 = n3 = n
Видно, что в данном случае эквивалентное число циклов получилось почти в четыре раза меньше того числа, которое получилось бы при постоянной нагрузке.
В заключение отметим, что для однородной структуры материала (нормализация, улучшение, объемная закалка) коэффициент KHL ограничивают в пределах: 1,0 ≤ KHL ≤ 2,6.
В случае поверхностной закалки, цементации и азотирования:
1,0 ≤ KHL ≤ 1,8.
2.3 Допускаемые изгибные напряжения.
При расчете зубьев на изгиб допускаемое изгибное напряжение может быть определено по формуле:
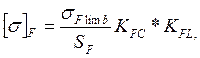
где σF limb - базовый предел выносливости материала колеса по изгибным напряжениям для пульсирующего никла (П-го цикла), значения которого приведены в табл. 8.
SF - коэффициент безопасности. Рекомендуется Sp = 1,7...2,2 (причем верхние значения - для литых заготовок); КFC - коэффициент, учитывающий влияние двухстороннего приложения нагрузки (например, реверсивные передачи). При односторонней нагрузке КFC = 1. При двухсторонней нагрузке КFC = 0,7,..0,8 (большие значения при НВ > 350); KFL - коэффициент долговечности.
Табл. 8
| № | Термообработка или химико- | Твердость | σF lim b |
| пп | термическое упрочнение | ||
| I. | Нормализация или улучшение | НВ ≤ 350 | 1,8 HB НВ |
| 2. | Объемная закалка | HRC = 45...55 | |
| 3. | Поверхностная закалка | HRC = 48...58 | 600…700 ...700 |
| (в сердцевине НВС = 25...35) | |||
| 4. | Цементация | HRC = 56...62 | 750…850 ...8Ь0 |
| (в сердцевине HRC = 32...45) | |||
| б. | Азотирование | HRC = 55...70 | + I2HHC* |
| (в сердцевине НРС = 24...40) | _ твердость | ||
Коэффициент долговечности определяется:
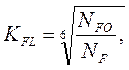- при НВ ≤ 350,
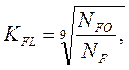- при НВ > 350.
Здесь: NFO- базовое число циклов. Для всех сталей NFO = 4*10^6;
NF - число циклов нагружения зубьев шестерни и колеса.
При постоянной нагрузке NFO = 60nt,
При переменной нагрузке подсчитывается эквивалентное число циклов нагружения зубьев:
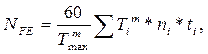
где m = 6 при НВ ≤ 350, m = 9 при НВ > 350.
В заключение укажем на некоторые ограничения на величину КFL:
1,0 ≤ KFL < 2 при НВ ≤ 350; 1,0 ≤ KFL < 1,6 при НВ > 350.
2.4 Расчет на контактную прочность.
При проектном расчете закрытых прямозубых и косозубых цилиндрических зубчатых передач основные размеры этих передач определяются расчетом на контактную прочность.
2.4.1 Если колесо и шестерню предполагается изготовить из стали, то расчетные формулы, разрешенные относительно межосевого расстояния aw, имеют следующий вид:
для прямозубых передач
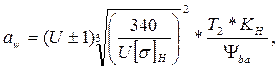мм;
для косозубых передач
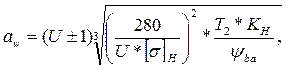мм
В этих формулах:
U - передаточное число рассчитываемой передачи;
[б]Н - допускаемое контактное натяжение для материала шестерни или колеса (менее прочного), Н/мм);
ψва - относительная ширина передачи, выбираемая в пределах:
ψва = 0,2...0,4 - для прямозубых передач,
ψва - 0,2...0,6 - для косозубых передач.
Причем меньшие значения принимаются для быстроходной ступени, а большие - для тихоходной ступени;
T2 - момент на колесе рассчитываемой передачи, Н·мм (моменты на всех валах привода были найдены в разделе I);
Кн - коэффициент нагрузки для расчета по контактном напряжениям, представляющий собой произведение двух коэффициентов:
KH = KHB · KHV, где KHB - коэффициент неравномерности распределения нагрузки по длине контакта
KHV - коэффициент динамической нагрузки.
Коэффициент неравномерности распределения нагрузки при расчете по контактным напряжениям (KHB) при переменной нагрузке может быть взят из графиков, представленных на рис.1, где ψbd = b/d1 (при проектных расчетах полезно использовать зависимость ψbd= ψba·(U±1)/2). В схеме соосного редуктора уточнить входной и промежуточный валы. При постоянной нагрузке KHB = 1,0.
Значения коэффициента динамической нагрузки при расчете по контактным напряжениям (KHV) приведены в табл. 9 (в числителе для прямозубых, в знаменателе - для косозубых передач).
Табл. 9
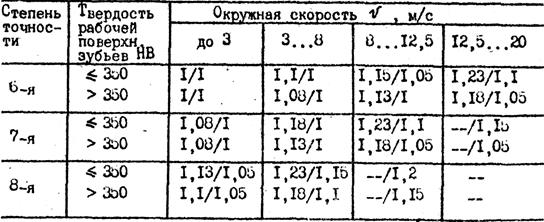
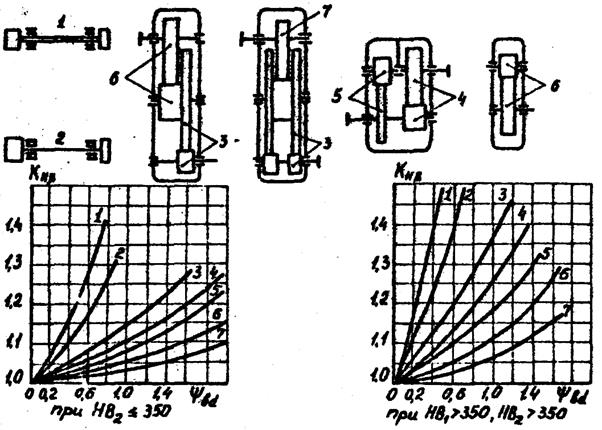
Рис. 1
При этом, если хотя бы для одного из зубчатых колес пары НВ ≤ 350, в таблице твердость рабочей поверхности зубьев НВ следует принять ≤ 350. В передачах общего машиностроения, которые встречаются в курсовом проектировании, предпочтительно назначать 7 или 8-ю степень точности.
Для предварительных расчетов можно принимать:
Кн = Кнβ*Kнν = 1.3...1.5.
Меньшие значения следует выбирать при расположении колес на валах, близком к симметричному (у середины пролета), большие значения - при несимметричном.
В нашем курсовом проекте студенту рекомендуется проектировать нестандартный редуктор. Поэтому межосевое расстояние aw, полученное расчетом на контактную прочность /по формуле (I) или (2)/, округлять до стандартного значения не требуется.
Дальнейший расчет передачи по определению всех основных параметров рассчитываемой передачи рекомендуется проводить в следующем порядке.
2.4.2 Задаются числом зубьев шестерни z1 и определяют число зубьев колеса z2= z1·U.
В прямозубых передачах число зубьев шестерня можно задать
z1 = 20…30
В косозубых передачах, задаваясь числом зубьев шестерни z1, следует помнить следующее. В случае косозубой передачи для более полного использования преимуществ косозубых колес желательно, чтобы в косозубых передачах соблюдалось неравенство
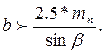
Это условие выполняется, если число зубьев шестерни взять
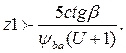
2.4.3 Определяют модуль зацепления:
для прямозубых передач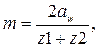 
для косозубых передач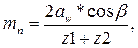 
где β - угол наклона зубьев, принимаемой β = 8°...20°.
Полученное значение модуля округляют до ближайшего стандартного по ГОСТ 9оСЗ_80 (таблица).
Таблица
Ряд стандартных модулей зубчатых передач по ГОСТ 9563_80
| 0,3 | (2,75) | 4,5 | ||
| 0,4 | 1,25 | |||
| 0,5 | 1,5 | (3,25) | 5,5 | |
| 0,6 | 1,75 | 3,5 | ||
| 0,7 | (3,75) | 6,5 | ||
| 0,8 | 2,25 | |||
| 2,5 | (4,25) |
Примечание. Значение модулей, указанные в скобках, применять нежелательно
2.4.4 После округления модуля до стандартного значения нужно уточнить межосевое расстояние:
для прямозубых передач aw = m/2(z1+z2);
для косозубых передач aw = mn/2cosβ(z1+z2);
2.4.5 Определяют диаметры колес:
для прямозубых передач
d1(2) = m·z1(2) - делительные диаметры шестерни (колеса);
da1(2) = d1(2)+2m - диаметры- вершин шестерни (колеса);
df1(2) = d1(2)-2.5m - диаметры впадин шестерни (колеса);
для косозубых передач
d1(2) = mn·z1(2)/cosβ - делительные диаметры шестерни (колеса);
da1(2) = d1(2)+2mn - диаметры вершин шестерни (колеса);
df1(2) = d1(2)-2.5mn - диаметры впадин шестерни (колеса).
Примечание. Формулы справедливы для зубчатых передач без смещения или при суммарном смещении XE = 0.
2.4.6 Определяется ширина колеса b = ψba·aw.
Ширина шестерни обычно выполняется несколько больше (на 2-3 мм) ширины колеса для компенсации возможных неточностей сборки.
2.4.7 Подсчитывается окружная скорость в зацеплении
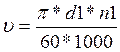м/с, где d1 – в мм; n1- в об/мин.
2.4.8 По данной скорости в соответствии с табл. уточняется значение коэффициента KHV, а затем KH = KHB · KHV.
2.4.9 В соответствии с уточненными значениями межосевого расстояния аw и коэффициента нагрузки KH производим проверку фактических контактных напряжений по формулам:
для прямозубой передачи для косозубой передачи
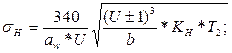(1) 
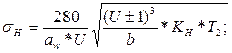(2)
В формулах (1) и (2) аw и b - в мм, Т2 - в Н*мм, бН и [б]Н - в Н/мм2. При этом превышение бН сверх [б]Н до 5% допускается. При большей разнице требуется пересчет межосевого расстояния.
2.5 Расчет закрытой цилиндрической зубчатой передачи заканчивается проверкой прочности зубьев на изгиб. Проверка прочности зубьев на изгиб проводится по формулам:
для прямозубой передачи для косозубой передачи
() 
()
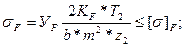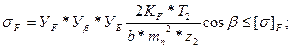В этих формулах: b, m, mn, T2, z2 - ширина передачи, мм;
модуль передачи, мм; момент на колесе рассчитываемой передачи, Н·мм;
число зубьев колеса - величины, найденные ранее,
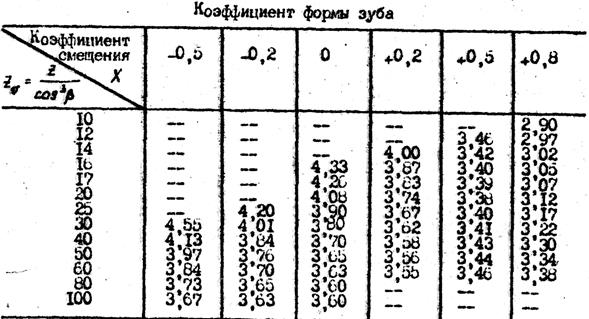
УF - коэффициент, учитывающий форму зуба. Этот коэффициент может быть найден в табл. 10 или с помощью кривых, приведенных на рис., по числу зубьев шестерни или колеса (см.ниже примечание). В случае косозубой передачи УF берется по эквивалентному числу зубьев zV = z/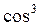 
β;
Уβ - коэффициент, учитывающий наклон зубьев. Для определения
этого коэффициента можно воспользоваться формулой: Уb = 1-b/140,
где b - угол наклона зуба, принимаемый в косоpубой передаче в пределах 8°...20°;
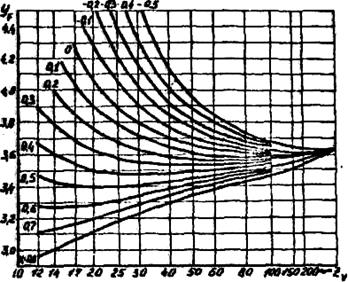
График для определения коэффициента УF
УE - коэффициент, учитывающий участие в зацеплении косозубой передачи нескольких пар зубьев. Этот коэффициент можно принять:
УE = 1/0,9Eα, где Eα - торцовый коэффициент перекрытия, равен:
Eα = [1.88-3.2(1/z1+1/z2)]cos β;
KF – коэффициент нагрузки для расчета по изгибным напряжениям, представляющий собой произведение двух коэффициентов:
KF = KFB · KFV, коэффициент неравномерности распределения нагрузки по длине контакта, KFV - коэффициент динамической нагрузки.
Коэффициент неравномерности распределения нагрузки при расчете по изгибным напряжениям (KFB) при переменной нагрузке может быть взят из графиков, представленных на рис.. При постоянной нагрузке KFB = 1,0.
Причем, коэффициент KFB в этих графиках дается в зависимости от относительной ширины: ψbd = b/d1.
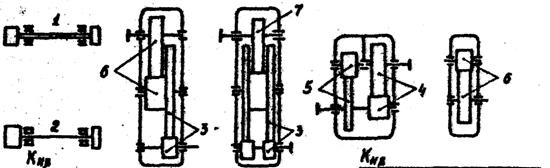
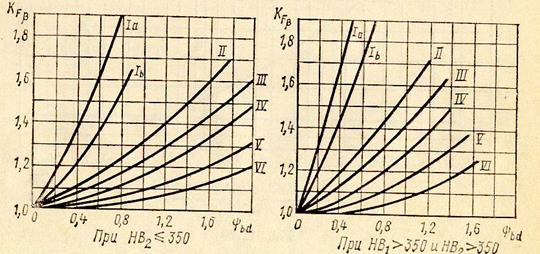
Значения коэффициента динамической нагрузки при расчете зубьев на изгиб (KFV) приведены в табл. 11 (в числителе - для прямозубых, в знаменателе - для косозубых передач). При этом, если хотя бы для одного из зубчатых колес пары НВ ≤ 350, в таблице твердость рабочей поверхности зубьев НВ следует принять ≤ 350. [σ]F - допускаемое изгибное напряжение для материала шестерни или колеса (см.ниже примечание), H/мм2. (см.раздел 3).
Примечание. Если для шестерни и колеса берется одинаковый материал, при проверке изгибных напряжений по формулам () и () коэффициент УF и допускаемое напряжение [σ]F берутся для шестерни.
Если материал для шестерни назначается более прочный, чем материал колеса, проверку ведут для того из колес, для которого меньше отношение [σ]F / УF.
Табл. 11
2.6 КОНСТРУКЦИЯ ШЕСТЕРЕН И КОЛЕС
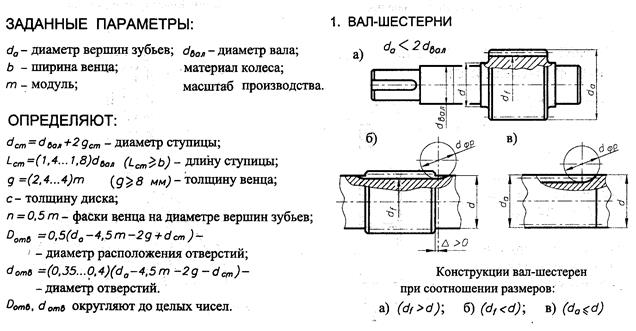
Рис.2
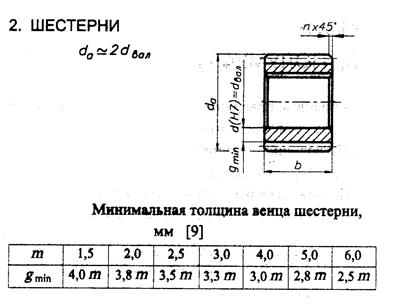
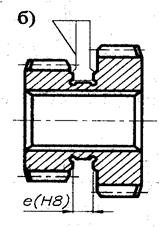
Рис.3
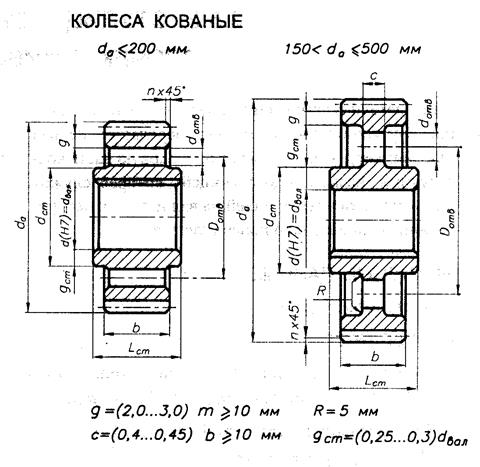
Рис.4
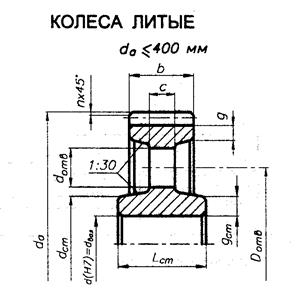
Рис.5
Стандартами (ГОСТ 1643-81 и ГОСТ 1758-81) установлены 12 степеней точности изготовления цилиндрических и конических зубчатых колес и передач (1-я степень - наивысшая, 12-я степень – наименьшая).
Выбор степени точности определяется условиями работы и назначением колес.
В табл.12 приведены ориентировочные значения предельных окружных скоростей колес в силовых передачах различной степени точности. В общем машиностроении колеса передач выполняют по 8-й или 9-й степени точности, а колеса ответственных передач - по 6-й или 7-й степени точности.
В особо ответственных тяжело нагруженных и высокооборотных передачах вертолетов, самолетов и других машин используют колеса по 4-й и 6-й степеням точности.
Таблица 12
Предельные окружные скорости для силовых передач, м/c
| Степень точности | Прямые зубья в передачах | Непрямые зубья в передачах | ||
| цилиндрич. | конической | цилиндрич. | конической | |
| 5 и более | св.15 | св.12 | св.30 | св.20 |
| до 15 | до 12 | до 30 | до 20 | |
| до 10 | до 8 | до 15 | до 10 | |
| до 6 | до 4 | до 10 | до 7 | |
| до 2 | до 1,5 | до 4 | до 3 |
Для предотвращения заклинивания зубьев допуском на межосевое расстояние (наряду с допуском на толщину зубьев) в зацеплении обеспечивается гарантированный минимальный боковой зазор.
Размер бокового зазора регламентируется видом сопряжения зубчатых колес. ГОСТ 1643-81 устанавливает шесть видов сопряжений зубчатых колес в передаче Н,Е,D,C,B,A (в порядке увеличения бокового зазора):
Н - нулевой минимальный зазор;
Е - малый зазор;
D и C - уменьшенный зазор;
В - нормальный зазор;
А - увеличенный зазор.
Устанавливаются шесть классов отклонений межосевого расстояния, обозначаемых в порядке убывания точности римскими цифрами от I до VI.
Рекомендуемые сочетания вида сопряжения и класса отклонений межосевого расстояния приведены в табл.13
Таблица 13
Предельные отклонения межосевого расстояния (мкм)
| Вид со- пряжения | Класс отлонений межосевого расстояния. | М е ж о с е в о е р а с с т о я н и е, мм | ||||||
| до 80 | св.80 до 125 | св.125 до 180 | св.180 до 250 | св.250 до 135 | св.315 до 400 | св.400 до 500 | ||
| -- | I | ±10 | ±11 | ±12 | ±14 | ±16 | ±18 | ±20 |
| H,E | II | ±16 | ±18 | ±20 | ±22 | ±25 | ±28 | ±30 |
| D | III | ±22 | ±28 | ±30 | ±35 | ±40 | ±45 | ±50 |
| C | IV | ±35 | ±45 | ±50 | ±55 | ±60 | ±70 | ±80 |
| B | V | ±60 | ±70 | ±80 | ±90 | ±100 | ±110 | ±120 |
| A | VI | ±100 | ±110 | ±120 | ±140 | ±160 | ±180 | ±200 |