Программное обеспечение вычислительной техники и автоматизированных систем

ЛАБОРАТОРНАЯ РАБОТА 10 ПО ДИСЦИПЛИНЕ

 

“Информационная безопасность”

Тема: Электронная цифровая подпись

 

 

Специальность: 230105

Программное обеспечение вычислительной техники и автоматизированных систем

 

Санкт-Петербург

Лабораторная работа

Электронная цифровая подпись

Цель работы

Ознакомиться со схемами цифровой подписи и получить навыки создания и проверки подлинности ЦП.

Указание к работе

На протяжении многих веков при ведении деловой переписки, заключении контрактов и оформлении любых других важных бумаг подпись ответственного лица или исполнителя была непременным условием признания его статуса или неоспоримым свидетельством его важности. Подобный акт преследовал две цели:

· гарантирование истинности письма путем сличения подписи с имеющимся образцом;

· гарантирование авторства документа (с юридической точки зрения).

Выполнение данных требований основывается на следующих свойствах подписи:

· подпись аутентична, т.е. с ее помощью получателю документа можно доказать, что она принадлежит подписывающему;

· подпись служит доказательством, что только тот человек, чей автограф стоит на документе, мог подписать данный документ, и никто другой не смог бы этого сделать;

· подпись непереносима, т.е. является частью документа и поэтому перенести ее на другой документ невозможно;

· документ с подписью является неизменяемым, т.е. после подписания его невозможно изменить, оставив данный факт незамеченным;

· подпись неоспорима, т.е. человек, подписавший документ, в случае признания экспертизой, что именно он засвидетельствовал данный документ, не может оспорить факт подписания;

· любое лицо, имеющее образец подписи, может удостовериться в том, что данный документ подписан владельцем подписи.

С переходом к безбумажным способам передачи и хранения данных, а также с развитием систем электронного перевода денежных средств, в основе которых – электронный аналог бумажного платежного поручения, проблема виртуального подтверждения аутентичности документа приобрела особую остроту. Развитие любых подобных систем теперь немыслимо без существования электронных подписей под электронными документами. Однако применение и широкое распространение электронно-цифровых подписей (ЭЦП) повлекло целый ряд правовых проблем. Так, ЭЦП может применяться на основе договоренностей внутри какой-либо группы пользователей системы передачи данных, и в соответствии с договоренностью внутри данной группы ЭЦП должно иметь юридическую силу. Но будет ли электронная подпись иметь доказательную силу в суде, например, при оспаривании факта передачи платежного поручения?

Схема 1

Данная схема предполагает шифрование электронного документа (ЭД) на основе симметричных алгоритмов и предусматривает наличие в системе третьего лица (арбитра), пользующегося доверием участников обмена подписанными подобным образом электронными документами. Взаимодействие пользователей данной системой производится по следующей схеме (см. рисунок 1)

Рисунок 1 – Основные методы построения схем ЭЦП. Схема 1

Участник A зашифровывает сообщение своим секретном ключе K_A, знание которого разделено с арбитром (С на рисунке 1), затем шифрованное сообщение передается арбитру с указанием адресата данного сообщения (информация, идентифицирующая адресата, передается также в зашифрованном виде).

Арбитр расшифровывает полученное сообщение ключом К_А, производит необходимые проверки и затем зашифровывает его секретным ключом участника B (K_B). Далее зашифрованное сообщение посылается участнику B вместе с информацией, что оно пришло от участника A.

Участник B расшифровывает данное сообщение и убеждается в том, что отправителем является участник A.

Авторизацией документа в данной схеме считается сам факт шифрования электронного документа (ЭД) секретным ключом и передача зашифрованного ЭД арбитру. Основным преимуществом этой схемы является наличие третьей стороны, исключающей какие-либо спорные вопросы между участниками информационного обмена, то есть в данном случае не требуется дополнительной системы арбитража ЭЦП. Недостатком схемы является так же наличие третьей стороны и использование симметричных алгоритмов шифрования. На практике эта схема не получила широкого распространения.

Схема 2

Фактом подписания документа в данной схеме является шифрование документа секретным ключом его отправителя. Здесь используются асимметричные алгоритмы шифрования.

Рисунок 2 – Основные методы построения схем ЭЦП. Схема 2

Вторая схема используется довольно редко вследствие того, что длина ЭД может оказаться очень большой (шифрование асимметричным алгоритмом может оказаться неэффективным по времени), но в этом случае в принципе не требуется наличие третьей стороны, хотя она и может выступать в роли сертификационного органа открытых ключей пользователя.

Схема 3

Наиболее распространенная схема ЭЦП использует шифрование окончательного результата обработки ЭД хэш-функцией при помощи асимметричного алгоритма. Структурная схема такого варианта построения ЭЦП представлена на рисунке 3.

Рисунок 3 – Основные методы построения схем ЭЦП. Схема 3

Процесс генерации ЭЦП

Процесс генерации ЭЦП происходит следующим образом.

Участник A вычисляет хэш-код от ЭД. Полученный хэш-код проходит процедуру преобразования с использованием своего секретного ключа. После чего полученное значение (которое и является ЭЦП) вместе с ЭД отправляется участнику B.

Участник B должен получить ЭД с ЭЦП и сертифицированный открытый ключ участника A, а затем произвести расшифрование на нем ЭЦП, сам ЭД подвергается операции хэширования, после чего результаты сравниваются, и если они совпадают, то ЭЦП признается истинной, в противном случае ложной.

В настоящее время применяются несколько алгоритмов цифровой подписи:

· RSA (наиболее популярен);

· Digital Signature Algorithm, DSA (алгоритм цифровой подписи американского правительства, который применяют в стандарте цифровой подписи (Digital Signature Standard, DSS), также используется часто);

· алгоритм Эль-Гамаля (иногда можно встретить);

· алгоритм, который применяют в стандарте ГОСТ РЗ4.10–94 (в основе лежит DSA и является вариацией подписи Эль-Гамаля);

· так же существуют алгоритмы подписей, в основе которых лежит криптография эллиптических кривых; они похожи на все прочие, но в некоторых ситуациях работают эффективнее.

Электронная подпись RSA

Для осуществления подписи сообщения 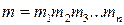необходимо вычислить хеш-функцию , которая ставит в соответствие сообщению m число y. На следующем шаге достаточно снабдить подписью только число y, и эта подпись будет относиться ко всему сообщению m.

Далее по алгоритму RSA вычисляются ключи (e, n) и (d, n).

Затем вычисляется s = y^d mod n (d – секретная степень).

Число s – это и есть цифровая подпись. Она просто добавляется к сообщению и получается подписанное сообщение < m, s >.

Теперь каждый, кто знает параметры подписавшего сообщение (т.е. числа e и n), может проверить подлинность подписи.

Для этого необходимо проверить выполнение равенства h (m) = s^e mod n.

Алгоритм Эль-Гамаля

Для генерации пары ключей сначала выбирается большое простое число p и два случайных числа g и x (g < p, x < p). Затем вычисляется y = g^x mod p.

Открытым ключом являются y, g и p. Закрытым ключом является x.

Чтобы подписать сообщение М, сначала выбирается случайное число k, взаимно простое с p – 1 (k – секретно). Затем вычисляется a = g^k mod p.

Из соотношения M = (xa + kb) mod (p –1) находится b. Выполнив преобразования, получим b = k ^–1(M – xa) mod (p –1), k ^–1∙ k ≡ 1 (mod (p –1)).

В результате подписью является пара (a, b). Для проверки подписи нужно убедиться, что y^a ∙ a^b mod p = g^M mod p.

ПРИМЕР

Пусть p = 11, g = 2, x = 8. Тогда y = 2⁸ mod 11 = 3. M = 5.

Выбираем k = 9. Тогда a = 2⁹ mod 11 = 6. 9∙ k ^–1 ≡ 1 (mod 10).

Для нахождения обратного элемента k ^–1 применяем расширенный алгоритм Евклида.

Нахождение обратного элемента с помощью расширенного алгоритма Евклида

 

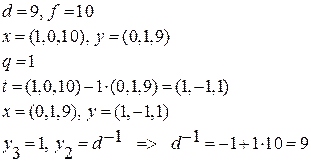
Теперь переходим обратно к алгоритму Эль-Гамаля.

Подписью сообщения M = 5 является пара (a, b) = (6, 3).

Проверка:

3⁶∙6³ mod 11 = 2⁵ mod 11.

Задание

Реализовать приложение, позволяющие решить задачи в соответствии с вариантом. Все параметры (сообщение, параметры, ключи) должны вводиться пользователем или задавать в файле.

Задачи

I. Для указанных открытых ключей пользователя RSA проверить подлинность подписанных сообщений:

1. .

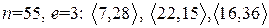2. .

3. .

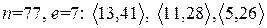4. .

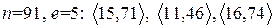5. .

II. Абоненты некоторой сети применяют подпись Эль-Гамаля с общими параметрами p = 23, g = 5. Для указанных секретных параметров абонентов найти открытый ключ y и построить подпись для сообщения m:

1. .

2. .

3. .

4. .

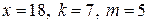5. .

Варианты

Примечание: Во всех вариантах предполагается, что h (m) = m для всех значений m.

Вариант	№№ задач		Вариант	№№ задач		Вариант	№№ задач
	I.1, II.1			I.1, II.5			I.2, II.3
	I.2, II.2			I.2, II.4			I.3, II.4
	I.3, II.3			I.4, II.2			I.4, II.5
	I.4, II.4			I.5, II.1			I.1, II.4
	I.5, II.5			I.1, II.2			I.5, II.2

Требования к оформлению отчёта

Отчёт должен содержать:

· титульный лист (обязат.);

· задание на лабораторную работу (обязат.);

· описание разработанного программного средства;

· описание проведённых исследований (обязат.);

· программный код, написанный непосредственно студентами (обязат.);

· тестирование программы.

Отчёт не должен содержать орфографических, пунктуационных и смысловых ошибок.

Все его разделы должны быть выдержаны в едином стиле оформления.

 

Контрольные вопросы

1. Для чего нужна цифровая подпись?

2. Назовите основные свойства цифровой подписи.

3. Какие схемы цифровой подписи существуют? Какая схема самая распространенная?

4. Как осуществляется подпись RSA? В чем отличие подписи RSA от шифра RSA?

5. Как осуществляется подпись Эль-Гамаля?

6. Как осуществляется проверка на подлинность подписи Эль-Гамаля?