Модель стоимости капитальных (долгосрочных) активов (САРМ) - одно из наиболее популярных теоретических построений в финансовом менеджменте, постоянно применяемое на практике при обосновании инвестиционных решений.
Согласно модели стоимости долгосрочных (капитальных) активов (САРМ), ожидания инвесторов складываются под воздействием двух факторов: степени инвестиционного риска, присущего приобретаемым акциям и цены за риск, которая устанавливается на финансовом рынке и определяется в процентах ожидаемой доходности.
САРМ используется для оценки требуемого уровня доходности инвестиционного портфеля для инвестора, который способен с помощью диверсификации избавиться от несистематического риска и который, таким образом, предполагает получить определенный уровень доходности как вознаграждение за принятый систематический риск.
САРМ также дает возможность оценить ставку дисконта, инвестиционного проекта, базируясь на его систематическом риске. Таким образом, модель дает ключ к сопоставлению проектов различных классов рискованности.
Как и всякая теоретическая модель, САРМ исходит из ряда допущений, не вполне согласующихся с реальной практикой:
САРМ предполагает, что инвесторы владеют хорошо диверсифицированными портфелями (т.е она не принимает во внимание несистематический риск, предполагая, что рационально мыслящий и действующий инвестор не вкладывает все деньги в один актив, а диверсифицирует свои инвестиции);
САРМ является равновесной моделью для совершенного рынка капитала и игнорирует действие таких эффектов, как налогообложение, разница в доступности информации для разных инвесторов, трансакционные издержки, различия ставок по кредитам и депозитам. Также предполагается, что все инвесторы на рынке мыслят, сходным образом и измеряют время в одних единицах;
|
|
САРМ основана на предположении, что среднерыночная доходность равна доходности биржевого индекса, а доходность долгосрочных дисконтных государственных ценных бумаг является безрисковой.
Выясним, как зависит требуемый уровень доходности на вложенный капитал от систематического риска?
Можно предложить следующие рассуждения. Если инвестиция является безрисковой, то соответствующий ей коэффициент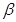 
= 0 (отсутствие риска), а ставка требуемой доходности равна безрисковой ставке Rf.
Если инвестиция имеет такой же риск, как и рынок в среднем, то для нее 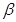= 1, а ставка требуемой доходности равна ожидаемой доходности по рынку в целом. На практике такая доходность, обозначаемая Rm, принимается равной ожидаемой доходности биржевого индекса, характеризующего рынок.
По теории, зависимость требуемого уровня доходности от систематического риска линейная, с увеличением риска (т.е. бета-фактора) повышаются и требования к доходности (Е(г).
Это позволяет построить график зависимости требуемого уровня доходности от систематического риска (рис.).
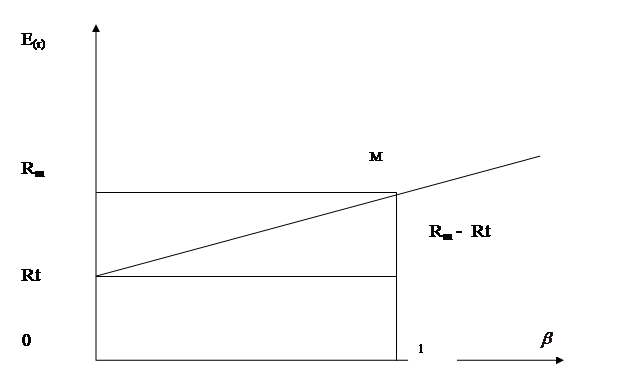
Уравнение этой прямой выглядит следующим образом:
По нему, зная коэффициент систематического риска 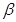, для любой ценной бумаги или инвестиционного портфеля можно найти требуемый уровень доходности Е(г).
Альфа-фактор, или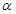 
, является мерой недооцененности ценной бумаги или портфеля в целом в фундаментальном анализе. Альфа-фактор показывает, насколько реально ожидаемая доходность от инвестиции (позитивная доходность FR) больше или меньше доходности, которая требуется в соответствии с условиями рынка (нормативной доходности по САРМ):
|
|
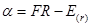, или 
Интерпретация 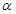проста:
если 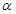> 0 — ценная бумага недооценена. По отношению к ней рекомендуется занять длинную позицию, т.е. покупать или играть на повышение;
если 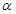= 0 - ценная бумага адекватно оценена;
если 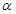< 0 — ценная бумага переоценена (уровень вознаграждения за риск не соответствует величине риска). По отношению к ней рекомендуется короткая позиция (игра на понижение или продажа).