Цепь переменного тока содержит различные элементы (активные сопротивления, индуктивности и емкости), образующие две параллельные ветви. Схема электрической цепи представлена на рисунке.
Начертить схему цепи, содержащую только те элементы, численные значения которых даны по Вашему варианту в таблице.
Определить индуктивность L и емкость С, если они имеются в схеме, токи в ветвях I1, I2 и в неразветвленной части цепи I методом проводимостей.
Вычислить коэффициент мощности cosφ, активную P, реактивную Q и полную S мощности цепи.
Начертить векторную диаграмму напряжений и токов.
Пример
Полные сопротивления ветвей:
а) активная
б) реактивная (емкостная)
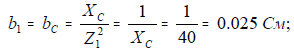
в) полная
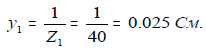
2 Проводимости второй ветви:
а) активная
б) реактивная (емкостная)
в) полная
3 Проводимости всей цепи:
а) активная
б) реактивная (емкостная)
в) полная
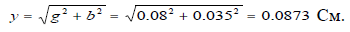
4 Токи ветвей:
5 Ток в неразветвленной части цепи:
6 Угол сдвига фаз между током и напряжением:
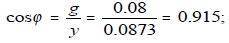
φ = arcсos 0.915 = 23,8°, т. к. индуктивная проводимость больше емкостной проводимости (bL>bC), то напряжение опережает ток на угол φ=23,8°.
7 Мощность цепи:
а) активная
б) реактивная
в) полная
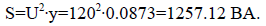
8 Векторную диаграмму проще строить по составляющим токов ветвей, определим их:
9 Длины векторов токов в масштабе MI =2,4 А/см:
10 При построении векторной диаграммы за основной принимаем вектор напряжения, а векторы токов располагаем около него под соответствующими углами сдвига фаз: векторы активных токов совпадают с вектором напряжения, емкостных – опережают на
90°, индуктивных – отстают на 90°. Общий ток равен геометрической сумме токов ветвей
.
Выражение синусоидальных величин комплексными числами.
|
|
2. Синусоидальный ток i=Im sin(ω t +ψ i) может быть изображен на комплексной плоскости (рис.7). Величина и направление вектора Im определяются координатами одной точки комплексной плоскости Im и этот вектор записывается с помощью комплексного числа:
3. 
,
4. 
- вектор вращается со скоростью ω против часовой стрелки;
5. 
- положение вектора при t=0 (начальное положение).
6. 
и можно опустить как постоянные составляющие, тогда получаем комплексное действующее число (комплекс тока) в показательной форме:
7. 
8. 
9. 
+j
10. 
Im
11. Im(Im)
12. +1
13. 
Ψi
14. 
O
15. Рис.7
16. Закон Ома в комплексной форме
17. 
Рис.8
18. Если на элементе электрической цепи присутствует напряжение u=Um sin(ω t +ψ u) и ток через него i=Im sin(ω t +ψ i), тогда
19. U =Uej 
20. I =Iej 
21. φ=ψ u -ψ i
22. 
23. Здесь
24. 
- полное комплексное сопротивление цепи переменного тока в показательной форме записи;
25. 
- модуль полного сопротивления;
26. φ - разность фаз между напряжением и током.
27. Z =z(cosφ + jsinφ) = R + jX - алгебраическая форма записи полного сопротивления.
28. R – вещественная часть комплексного числа, активное сопротивление;
29. Х – мнимая часть комплексного числа, реактивное сопротивление.
30. Проводимость цепи:
31. 
32. 
- полная комплексная проводимость цепи переменного тока в показательной форме записи;
33. 
- модуль полной проводимости;
34. Y =y[cos(-φ) + jsin(-φ)] = ycosφ - jysinφ = G + jB - алгебраическая форма записи полной проводимости.
35. G – вещественная часть, активная проводимость;
36. B – мнимая часть, реактивная проводимость.