Теорема 4 (свойства бесконечно малых функций).

Свойства предела функции.

Теорема 1 (свойства предела функции).

1. Если $ lim _x ® af(x) = A, то найдется окрестность точки a 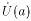такая, что в этой окрестности функция f (x) будет ограничена.
2. Если f (x) есть постоянная A в некоторой окрестности точки a, то lim _x ® af (x) = A
3. Если lim _x ® af (x) = A 1 и lim _x ® af (x) = A 2, то A 1 = A 2

Утверждения данной теоремы вытекают из определения предела функции.

Теорема 2 (арифметические операции над пределами). Если lim _x ® af (x) = A, lim _x ® ag (x) = B, то

1. lim _x ® a[f(x) ± g(x)]=A ± B,
2. lim _x ® af (x) g (x) = AB
3. lim _x ® af (x) /g (x) = A/B, B ¹ 0

Эта теорема непосредственно следует из соответствующей теоремы о пределах последовательностей.

Теорема 3 (предел и неравенства). Пусть f:E ® R, g:E ® R, h:E ® R

1. Если lim _x ® af (x) = A, lim _x ® ag (x) = B и A<B, то $ 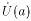: " x Î 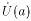f (x) <g (x).
2. Если для " x Î E f (x) £ g (x) £ h (x) и существует lim _x ® af (x) = lim _x ® ah (x) = A. то существует lim _x ® ag (x) = A

Пример 6. (Первый замечательный предел)

lim _x ® 0(sin x) /x = 1

Доказательство.

1. Покажем, что

cos ² x< (sin x) /x< 1 при 0 <|x|< p / 2.

Так как cos²x,(sin x)/x - четные функции, то достаточно рассмотреть случай 0<x<p/2. Из рис. 15 и определения функций cos x и sin x, сравнивая площади сектора 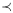OCD, треугольника D OAB и сектора 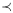OAB, найдем

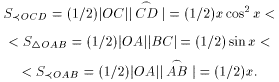
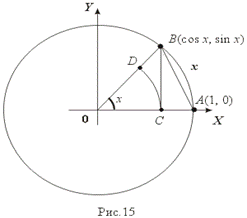
Разделив эти неравенства на (1/2) x, получим требуемый результат.

1. Из выше полученного результата следует, что

| sin x| £ |x| " x Î R.

1. Из 2) по теореме о предельном переходе в неравенствах вытекает, что

lim _x ® 0sin x = 0.

1. Теперь покажем, что

lim _x ® 0(sin x) /x = 1.

Cчитая, что |x|<p/2, в силу полученного в 1) неравенства имеем

1-sin² x< sin x/x< 1.

Но lim_{x® 0}(1-sin ²x) = 1, значит, по теореме о предельном переходе в неравенствах следует, что

lim _x ® 0(sin x) /x = 1.

Следствие 1.

lim _x ® 0(tgx) /x = 1
lim _x ® 0(arcsin x) /x = 1
lim _x ® 0 (arctgx) /x = 1

Пример 7. Найти

1. lim_{x® 0}(sin 6x)/4x;
2. lim_{x® 0}(1-cos x)/x².

Решение.

lim _x ® 0(sin 6 x) / 4 x = (3 / 2) lim _x ® 0(sin 6 x) / 6 x = 3 / 2;
lim _x ® 0(1-cos x) /x 2 = lim _x ® 0 (2sin² x/ 2) /x 2 =
= (1 / 2)lim _x ® 0(sin² x/ 2) / (x/ 2)² = 1 / 2.

Пример 8. (Второй замечательный предел)

e = lim _x ® ¥(1+1 /x) ^x

Как получена данная формула можно найти в книге Зорича В.А.
"Математический анализ" ч.1.

Если в данной формуле положить y = 1/x, то получим вторую запись данной формулы.

lim _x ® 0(1 +x)^{1 /x} = e.

Пример 9. Найти

1. lim_{x® ¥}(1+5/x)^3x;
2. lim_{x® 0}(1-3x)^2/x.

Решение.

1. lim _x ® ¥(1+5 /x)^{3 x} = lim _x ® ¥ (1+5 /x)^{(x/ 5)(5 /x)(3 x)} = lim _x ® ¥(1+5 /x)^{(x/ 5)15} = e 15;
2. lim _x ® 0(1-3 x)^{2 /x} = lim _x ® 0(1-3 x)^{(-1 / (3 x))(-3 x) · (2 /x)} = lim _x ® 0(1-3 x)^{(-1 / (3 x))(-6)} = e^- 6.

Упражнение 1. Доказать теоремы 1,2,3.

Бесконечно малые и бесконечно большие функции.

Определение 8 (бесконечно малая функция). Функция называется бесконечно малой в точке a или при x ® a, если

lim _x ® af (x) = 0

Пример 10.
f (x) = 1 /x, x ® ¥
f (x) = x 2, x ® 0
f (x) = 1-cos x, x ® 0

Заметим, что если функция f(x) имеет предел в точке a, равный A, то функция a(x) = f(x)-A является бесконечно малой в точке a. То есть, если функция f(x) имеет предел A в точке a, то f(x) = A+a, где lim_{x® a}a (x) = 0.

Отметим некоторые свойства бесконечно малых функций.

Теорема 4 (свойства бесконечно малых функций).

1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
2. Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая.
3. Произведение конечного числа бесконечно малых является бесконечно малой.

Доказательство. Докажем для примера первое утверждение теоремы для двух бесконечно малых.

Из того, что существует lim_{x® a}a(x) = 0, следует, что " e>0 $ d₁(e)>0 такое, что " x: 0<|x-a|<d₁ выполняется неравенство
|a(x)|< e/2. Аналогично, из существования предела lim_{x® a} b(x) = 0, следует " e>0 $ d₂(e)>0 такое, что " x: 0<|x-a|<d₂
выполняется неравенство |b(x)|< e/2. Тогда " x: 0<|x-a|<d = min{d₁,d₂} выполнятся оба неравенства одновременно, то есть

| a(x)+b(x) | £ | a(x) |+| b(x) |< e.

Определение 9 (бесконечно большая функция). Функция называется бесконечно большой при x ® a или в точке a, если для любого положительного числа e найдется такое положительное d(e), что для всех x¹ a и удовлетворяющих условию |x-a|<d будет выполнено неравенство |f(x)|>e.

Аналогично можно дать определение бесконечно большой при x® ¥. Приведем его в символической записи:

lim _x ® ¥ f (x) = ¥ Û " e>0 $ d(e)>0 " x:|x|> d |f (x) |> e.

Предложение 1. a(x) бесконечно малая функция при x ® a Û 1 / a(x) — бесконечно большая при x ® a

Пример 11. y = x² – бесконечно малая функция при x ® 0, а y = 1/x² – бесконечно большая при x ® 0.