Лекция 8. Простые числа
Простое число – натуральное число, большее единицы и не имеющее других натуральных делителей, кроме самого себя и единицы. Натуральное число – целое положительное число. Множество натуральных чисел обозначается 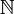 .
.
Основная теорема арифметики – любое натуральное число n, большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей.
n = p1e1 * p2e2 *... * pkek, (8.1)
где p1, p2, …, pk – простые сомножители;
e1, e2, …, ek – количество (степени) простых сомножителей.
Например, n = 600 = 23 * 31 * 52.
Теорема Евклида – простых чисел бесконечно много («Начала», книга IX, утверждение 20).
Возьмем ряд последовательных простых чисел (например, {2, 3, 5}) и перемножим их:
2 * 3 * 5 = 30.
Добавим к результату единицу:
2 * 3 * 5 + 1 = 30 + 1 = 31.
Если разделить 31 на любое простое число из этого ряда (2, 3 или 5), то в остатке получится 1:
31 mod 2 = 1,
31 mod 3 = 1,
31 mod 5 = 1.
Это означает, что число 31 не делится на числа ряда. Такие рассуждения справедливы и в общем случае: если взять ряд последовательных простых чисел, перемножить их и добавить единицу, то полученное число не будет делиться ни на одно из исходных простых чисел. Число 31 тоже простое число, но его нет в первоначальном списке, который, следовательно, является неполным.
Возьмем следующий ряд чисел в качестве примера - {2, 3, 5, 7, 11, 13}, перемножим их и добавим единицу:
2 * 3 * 5 * 7 * 11 * 13 + 1 = 30 030 + 1 = 30 031,
Результат не является простым числом, так как может быть разложен в произведение двух других чисел:
30 031 = 59 * 509,
Согласно основной теоремы арифметики любое натуральное число может быть единственным образом разложено в произведение простых множителей. В случае с числом 30 031, которое является составным числом, ясно, что для его разложения в произведение простых множителей чисел в списке {2, 3, 5, 7, 11, 13} будет недостаточно, т.е. этот список неполон.
Следствием теоремы Евклида является утверждение: каким бы ни был первоначальный ряд простых чисел, при их перемножении и добавлении единицы получается новое число одного из двух типов:
1. простое число, которого нет в списке;
2. составное число, при разложении которого на простые множители получаются простые числа, не входящие в список.
Таким образом, первоначальный ряд простых чисел всегда является неполным, если он не является бесконечно длинным.
Определение наибольшего общего делителя
Наибольшим общим делителем (НОД) для двух целых чисел m и n называется наибольший из их общих делителей (например, для чисел 70 и 105 НОД равен 35). НОД существует и однозначно определён, если хотя бы одно из чисел m или n отлично от нуля. Возможные обозначения наибольшего общего делителя чисел m и n:
- НОД(m, n);
- gcd(m, n) (англ. Greatest Common Divisor).
Наиболее известным способом определения НОД является алгоритм Евклида. Этот алгоритм не был открыт Евклидом, т.к. упоминание о нём имеется уже в «Топике» Аристотеля. В «Началах» Евклида он описан дважды - в VII книге для нахождения НОД двух натуральных чисел и в X книге для нахождения наибольшей общей меры двух однородных величин.
Суть алгоритма заключается в последовательном делении большего числа n на меньшее m, до тех пор, пока остаток от деления r не станет равным 0. При этом после каждого деления n присваивается текущее значение m, а m – остаток от деления r.
Описание алгоритма (при n ≥ m).
1. Если m = 0, то завершить работу, т.к. n является НОД.
2. r = n mod m, n = m, m = r и перейти к шагу 1.
Пример. n = 1071, m = 462.
Таблица 8.1. Таблица итераций

Результат – НОД(1071, 462) = 21.
Существует более мощный алгоритм определения НОД – расширенный алгоритм Евклида. Несмотря на то, что он медленнее, данный алгоритм помимо НОД позволяет найти два таких числа α и β, что
α n + β m = НОД. (8.2)
Данное выражение называется соотношением Безу.
Суть расширенного алгоритма аналогична стандартному – последовательное деление большего числа n на меньшее m, до тех пор, пока остаток от деления r не станет равным 0. При этом на каждой итерации дополнительно вычисляются:
- целая часть qi от деления ni на mi;
- αi = αi-2 – qi αi-1;
- βi = βi-2 – qi βi-1.
Для первой итерации принимаются α-1 = 1, α0 = 0, β-1 = 0, β0 = 1. Итоговые числа α и β равны α = αk-2, β = βk-2.
Описание алгоритма (при n ≥ m).
1. α-1 = 1, α0 = 0, β-1 = 0, β0 = 1, i = 1.
2. Если m = 0, то завершить работу, т.к. n является НОД, α = αk-2, β = βk-2.
3. r = n mod m, n = m, m = r, qi = ni div mi, αi = αi-2 – qi αi-1, βi = βi-2 – qi βi-1, i = i + 1 и перейти к шагу 2.
Пример. n = 1071, m = 462.
Таблица 8.2. Таблица итераций
Результат – НОД(1071, 462) = 21, α = -3, β = 7 → (-3) * 1071 + 7 * 462 = 21.
Расширенный алгоритм Евклида позволяет найти обратное (мультипликативно обратное) число по модулю.
Пусть даны модуль n и число m. Требуется обратное число m-1, такое, что
(m m-1) mod n = 1. (8.3)
Приведем следующее соотношение Безу
-α n + β m = 1. (8.4)
Это равенство означает, что для некоторого целого α имеет место равенство β m - α n = 1. Значит, мы можем вычислить m-1 (= β) с помощью расширенного алгоритма Евклида. При этом значение переменной α нас не интересует. Если число m-1 = β получается отрицательным, то нужно прибавить к нему n.
Пример. n = 97, m = 30.
Таблица 8.3. Таблица итераций

Т.к. m-1 – отрицательное число, то добавляем к нему n → m-1 = -42 + 97 = 55. Проверяем (m m-1) mod n = (30 * 55) mod 97 = 1.