Разложение функций в ряд Фурье.
Рассмотрим функцию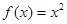 
, заданную на отрезке [0; 1].
1)Разложим эту функцию в полный тригонометрический ряд Фурье.
Здесь половина длины отрезка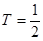 
. Поэтому полная ортогональная система тригонометрических функций в 
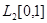имеет вид
1,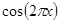 
, 
, …, 
, 
, …
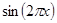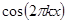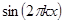(см. раздел 2 последней лекции).
Найдем коэффициенты разложения нашей функции по этой системе.
В соответствии с формулами (6) – (8) последней лекции, коэффициент при 1
.
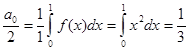Для вычисления остальных коэффициентов будем 2 раза использовать формулу интегрирования по частям.
Коэффициенты при косинусах
= 
=
= 
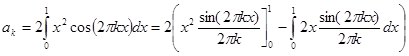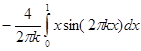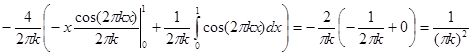
Коэффициенты при синусах
= 
= 
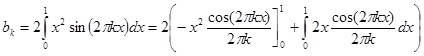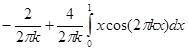
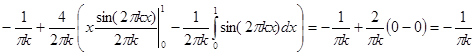
Итак, разложение нашей функции в полный ряд Фурье на отрезке [0; 1] имеет следующий вид
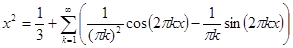
Частичные суммы этого ряда дают приближение нашей функции на [0; 1] тригонометрическими многочленами. В частности, первая частичная сумма
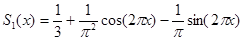
Квадрат нормы отклонения исходной функции от этой должен быть сравнительно небольшим положительным числом. Согласно формуле (9) из последней лекции
.
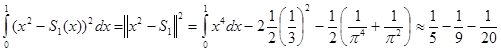Разложение функции в тригонометрический ряд Фурье иногда помогает найти точные значения сумм некоторых числовых рядов. Заметим, что при продолжении нашей функции с отрезка [0; 1] на [-1; 0] по периодичности, левосторонний предел в нуле будет равен 1, а правосторонний остается 0. Согласно Теореме Дирихле, наш ряд Фурье принимает в точке 0 среднее значение между этими пределами, то есть ½. Таким образом, подставив в наш ряд Фурье значение x=0, получим
.
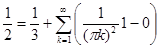Отсюда легко получается точное значение суммы обратных квадратов натуральных чисел
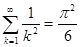
2)Разложим ту же функцию в тригонометрический ряд Фурье по косинусам.
Для этого продолжим нашу функцию на [-1; 0] по четности и разложим ее в ряд Фурье в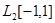 
. Здесь половина длины отрезка 
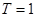и, вследствие четности в нашем разложении будут участвовать функции
|
|
1,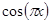 
, …, 
, …
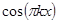При получении окончательных выражений для коэффициентов разложения будем использовать очевидные равенства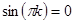 
и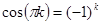 
при любом натуральном k.
В соответствии с формулой (11) последней лекции коэффициенты разложения
,
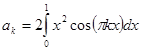В частности
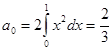, то есть коэффициент при 1 
.
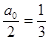При k>0
= 
=
= 
=
=- 
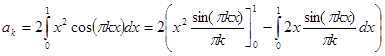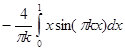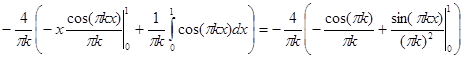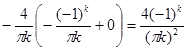
Итак, разложение нашей функции в ряд Фурье по косинусам имеет вид:
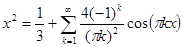
Сумма первых двух ненулевых слагаемых
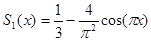
Найдем квадрат нормы невязки для этого приближения к функции в пространстве 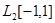. Согласно формуле (12) из последней лекции,
.
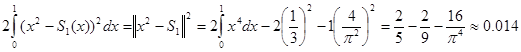Как и следовало ожидать, получилось относительно небольшое положительное число.
3)Разложим ту же функцию в тригонометрический ряд Фурье по синусам.
Для этого продолжим нашу функцию на [-1; 0] по нечетности и разложим ее в ряд Фурье в 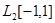. Половина длины отрезка 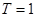и, вследствие нечетности в нашем разложении будут участвовать функции
, …, 
, …
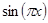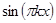В соответствии с формулой, приведенной в конце последней лекции, коэффициенты разложения по этим функциям вычисляются следующим образом:
= 
= 
= 
= 
=
= 
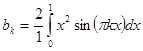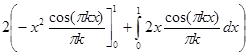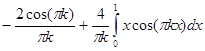
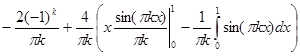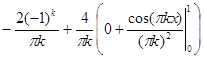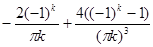
Итак, разложение нашей функции в ряд Фурье по синусам имеет вид:
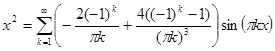
Сумма первых двух ненулевых слагаемых
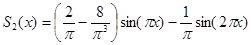
Найдем квадрат нормы невязки для этого приближения к функции в пространстве 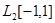. Согласно формуле (13) в конце последней лекции,
.
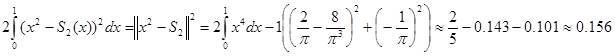Как и следовало ожидать, получилось относительно небольшое положительное число.
4) Домашнее задание по рядам Фурье.
Текст и варианты задания высылаю в отдельном файле. Разобранные выше примеры дают образец выполнения задания (кроме графиков): раздел 2 – для вариантов с продолжением функции по четности, раздел 3 – для вариантов с продолжением по нечетности. При построении графика всего ряда используйте Теорему Дирихле – в точках непрерывности внутри отрезка - совпадение с функцией, а в точках разрыва (и крайних точках отрезка при продолжении по периодичности) – середина “ступеньки”. График частичной суммы (строить на том же рисунке) должен быть гладким, его можно построить приблизительно – по нескольким точкам, где легко вычислить значение. Задание небольшое, срок выполнения – 1 неделя. Система распределения вариантов – прежняя.