1. В восемнадцатом веке деятельность математиков сосредоточивалась в области анализа и его приложений к механике. Самые крупные фигуры можно расположить как бы в виде генеалогического древа, указывающего на их интеллектуальное родство:
Лейбниц (1646–1716)
Братья Бернулли: Якоб (1654–1705), Иоганн (1667–1748)
Эйлер (1707-1783)
Лагранж (1736—1813)
Лаплас (1749-1827)
С трудами этих ученых тесно связана деятельность группы французских математиков, прежде всего Клеро, Даламбера и Мопертюи, которые в свою очередь были связаны с философами эпохи Просвещения. К ним надо добавить швейцарских математиков Ламберта и Даниила Бернулли. Научная деятельность в основном была сосредоточена в академиях, среди которых выдающееся место занимали Парижская, Берлинская и Петербургская. Преподавание в университетах имело меньшее значение, а то и никакого. Это был период, когда некоторые из ведущих европейских стран управлялись теми, кого, смягчая выражения, называют просвещенными деспотами: это Фридрих II, Екатерина II, пожалуй, и Людовики XV и XVI. Притязания этих деспотов на славу частично основаны на том, что они любили окружать себя учеными людьми. Такая любовь была чем-то вроде интеллектуального снобизма, но он умерялся в известной мере пониманием значения естествознания и прикладной математики в деле улучшения мануфактур и повышения боеспособности вооруженных сил. Например, говорят, что отличные качества французского флота связаны с тем, что при конструировании фрегатов и линейных кораблей кораблестроители частично основывались на математической теории. Работы Эйлера изобилуют применениями к вопросам, имеющим значение для армии и флота. Астрономия продолжала играть свою выдающуюся роль в качестве приемной матери математических исследований, пользуясь покровительством королей и императоров.
2. В Швейцарии Базель, свободный имперский город с 1263 г., уже долгое время был средоточием науки. Еще во времена Эразма его университет был важным центром. Науки и искусства процветали в Базеле, как и в голландских городах, под управлением купеческого патрициата. К этому базельскому патрициату принадлежала купеческая семья Бернулли, которая в предыдущем столетии переехала туда из Антверпена, когда этот город был захвачен испанцами. С конца семнадцатого столетия до настоящего времени эта семья в каждом поколении давала ученых. Воистину во всей истории науки трудно найти семью, поставившую более внушительный рекорд.
Родоначальниками этой династии были два математика, Якоб и Иоганн Бернулли. Якоб изучал теологию, Иоганн изучал медицину, но когда в лейпцигских Acta Eruditorum появились статьи Лейбница, оба они решили стать математиками. Они стали первыми выдающимися учениками Лейбница. В 1687 г. Якоб занял кафедру математики в Базельском университете, где он преподавал до своей смерти в 1705 г. Иоганн в 1697 г. стал профессором в Гронингене (Голландия), а после смерти брата перешел на его кафедру в Базеле, где преподавал сорок три года. Якоб начал переписываться с Лейбницем в 1687 г. Затем, постоянно обмениваясь мыслями с Лейбницем и между собой, не раз вступая в ожесточенное соперничество друг с другом, оба брата начали открывать те сокровища, которые содержались в путепролагающем достижении Лейбница. Список их результатов длинен и содержит не только многое из того, что сейчас входит в наши элементарные учебники дифференциального и интегрального исчисления, но и интегрирование ряда обыкновенных дифференциальных уравнений. Якобу принадлежит применение полярных координат, исследование цепной линии (уже рассмотренной Гюйгенсом и другими), лемнискаты (1694 г.) и логарифмической спирали. В 1690 г. он нашел так называемую изохрону, которую Лейбниц в 1687 г. определил как кривую, вдоль которой тело падает с постоянной скоростью, – оказалось, что это полукубическая парабола. Якоб также исследовал изопериметрические фигуры (1701 г.), что привело его к задаче из вариационного исчисления. Логарифмическая спираль, которая обладает свойством воспроизводиться при различных преобразованиях (ее эволюта – тоже логарифмическая спираль, и они обе по отношению к полюсу являются подошвенной кривой и каустикой), настолько обрадовала Якоба, что он пожелал, чтобы эту кривую вырезали на его могильном камне с надписью: eadem mutata resurgo (изменившись, возникаю такой же).
Якоб Бернулли был также одним из первых исследователей в теории вероятностей, и по этому предмету он написал «Искусство предположения» (Ars conjectandi) – книгу, опубликованную посмертно, в 1713 г. В ее первой части перепечатан трактат Гюйгенса об азартных играх, в остальных частях рассматриваются перестановки и сочетания, а главным, результатом является «теорема Бернулли» о биномиальных распределениях. При рассмотрении треугольника Паскаля в этой книге появляются «числа Бернулли».
3. Работы Иоганна Бернулли тесно связаны с работами его старшего брата, и не всегда легко различить их результаты. Иоганна часто рассматривают как изобретателя вариационного исчисления вследствие его вклада в задачу о брахистохроне. Это – кривая быстрейшего спуска для материальной точки, которая движется в поле тяготения от заданной начальной к заданной конечной точке, кривая, которую исследовали Лейбниц и оба Бернулли в 1697 и в последующие годы. В это время они открыли уравнение геодезических линий на поверхности. Решением задачи о брахистохроне является циклоида. Эта кривая решает также задачу о таутохроне – кривой, вдоль которой материальная точка в гравитационном поле достигает наинизшей точки за время, которое не зависит от исходной точки движения. Гюйгенс открыл это свойство циклоиды и использовал его для построения таутохронных часов с маятником (1673 г.), период колебания которого не зависит от амплитуды.
В числе других Бернулли, повлиявших на развитие математики, есть два сына Иоганна: Николай и, особенно, Даниил. Николай, как и Даниил, был приглашен в Петербург, незадолго до того основанный Петром Великим; там он пробыл недолго. Задача по теории вероятностей, которую он предложил, находясь в этом городе, известна как Петербургская задача (или, более выразительно, Петербургский парадокс). Этот сын Иоганна умер молодым, но другой сын, Даниил, дожил до глубокой старости. До 1777 г. он был профессором Базельского университета. Его плодовитая деятельность посвящена главным образом астрономии, физике и гидродинамике. Его «Гидродинамика» появилась в 1738 г., и одна из теорем этой книги, о гидравлическом давлении, носит его имя. В том же году он заложил основы кинетической теории газов; вместе с Даламбером и Эйлером он изучал теорию колебаний струн. Его отец и дядя развивали теорию обыкновенных дифференциальных уравнений, Даниил же был пионером в области уравнений в частных производных.
4. Из Базеля вышел также самый плодовитый математик восемнадцатого столетия, если только не всех времен, – Леонард Эйлер. Его отец изучал математику под руководством Якоба Бернулли, а Леонард – под руководством Иоганна. Когда в 1725 г. сын Иоганна Николай уехал в Петербург, молодой Эйлер последовал за ним и оставался в Петербургской академии до 1741 г. С 1741 по 1766 г. Эйлер находился в Берлинской академии под особым покровительством Фридриха II, а с 1766 до 1783 г. он снова в Петербурге, теперь уже под эгидой императрицы Екатерины. Он был дважды женат и имел тринадцать детей. Жизнь этого академика восемнадцатого столетия была почти целиком посвящена работе в различных областях чистой и прикладной математики. Хотя он потерял в 1735 г. один глаз, а в 1766 г. – второй, ничто не могло ослабить его огромную продуктивность. Слепой Эйлер, пользуясь своей феноменальной памятью, продолжал диктовать свои открытия. В течение его жизни увидели свет 530 его книг и статей; умирая, он оставил много рукописей, которые Петербургская академия публиковала в течение последующих 47 лет. Это довело число его работ до 771, но Густав Энестрем дополнил этот список до 886.
Эйлеру принадлежат заметные результаты во всех областях математики, существовавших в его время. Он публиковал свои открытия не только в статьях различного объема, но и в многих обширных руководствах, где упорядочен и кодифицирован материал, который собирали поколения. В некоторых областях изложение Эйлера было почти что окончательным. Например, наша нынешняя тригонометрия с ее определением тригонометрических величин как отношений и с принятыми в ней обозначениями восходит к «Введению в анализ бесконечных» (Introductio in analysin infinitorum, 1748 г.) Эйлера. Колоссальный авторитет его руководств привел к упрочению ряда его обозначений в алгебре и в анализе; Лагранж, Лаплас и Гаусс знали Эйлера и следовали за ним во всей своей деятельности.
«Введение» 1748 г. в своих двух томах охватывает немалое разнообразие вопросов. В нем содержится изложение бесконечных рядов, в том числе рядов для 
и соотношение 
(уже открытое Иоганном Бернулли и другими, в различных видах). Исследование кривых и поверхностей с помощью их уравнений ведется настолько свободно, что мы, можем рассматривать «Введение» как первый учебник аналитической геометрии. Мы находим здесь также алгебраическую теорию исключения. Наиболее увлекательными частями этой книги является глава о функции дзета и об ее связи с теорией простых чисел, равно как и глава о partitio numerorum (разбиении чисел на слагаемые).
Другим большим и богатым по содержанию руководством Эйлера было «Дифференциальное исчисление» (Institutiones calculi differentialis, 1755 г.), за которым последовали три тома «Интегрального исчисления» (Institutiones calculi integralis, 1768–1774 г.). Здесь мы находим не только наше элементарное дифференциальное и интегральное исчисление, но также теорию дифференциальных уравнений, теорему Тейлора со многими приложениями, формулу суммирования Эйлера и эйлеровы интегралы В и Г. Раздел о дифференциальных уравнениях с его разграничением «линейных», «точных» и «однородных» уравнений все еще является образцом для наших элементарных учебников по этому предмету. «Механика, или наука о движении, изложенная аналитически» (1736 г.) Эйлера была первым учебником, в котором ньютоновская динамика материальной точки была развита аналитическими методами. За ней последовала «Теория движения твердых тел» (1765 г.), в которой таким же образом трактуется механика твердых тел. Этот трактат содержит эйлеровы уравнения для тела, вращающегося вокруг точки. «Полное введение в алгебру» (1770 г.), написанное по-немецки и продиктованное слуге, стало образцом для многих позднейших учебников по алгебре. В нем изложение доведено до теории уравнений третьей и четвертой степени.
В 1744 г. появилось сочинение Эйлера «Метод нахождения кривых линий, обладающих свойствами максимума или минимума» (Methodus inveniendi lineas curvas maximi minimivi proprietate gaudentes). Это было первое изложение вариационного исчисления, оно содержало эйлеровы уравнения и многие приложения, включая открытие того, что катеноид и прямой геликоид являются минимальными поверхностями. Многие другие результаты Эйлера вошли в его работы меньшего объема, содержащие немало драгоценностей, ныне мало известных. В числе более известных его открытий теорема, связывающая число вершин (
), граней (
) и ребер (
) замкнутого многогранника (
), эйлерова прямая в треугольнике, кривые постоянной ширины (Эйлер называл их кривыми orbiformi) и эйлерова постоянная
Несколько статей посвящены занимательной математике (семь кёнигебергских мостов, задача о шахматном коне). Одни лишь результаты Эйлера в области теории чисел (к его открытиям в этой области принадлежит закон квадратичной взаимности) дали бы ему место в пантеоне славы. Деятельность Эйлера в значительной мере была посвящена астрономии, причем особое внимание он уделял теории движения Луны, этому важному разделу задачи трех тел. Его «Теория движения планет и комет» (Theoria motus planetarum et cometarum, 1774 г.) является трактатом по небесной механике. С этим трудом Эйлера связаны его исследования о притяжении эллипсоидов (1768 г.).
У Эйлера есть книги по гидравлике, по кораблестроению, по артиллерии. В 1769–1771 гг. появились три тома его «Диоптрики» (Dioptrica) с теорией преломления лучей в системе линз. В 1739 г. появилась его новая теория музыки, о которой говорили, что она слишком музыкальна для математиков и слишком математична для музыкантов. Философское изложение Эйлера наиболее важных проблем естествознания в его «Письмах к одной немецкой принцессе» (написаны в 1760–1761 гг.) остается образцом популяризации.
Огромная продуктивность Эйлера была и остается поводом для изумления и восхищения каждого, кто пытался изучать его труды, – задача не столь трудная, как это кажется, так как латынь Эйлера очень проста и его обозначения почти современны, – пожалуй, было бы лучше сказать, что наши обозначения почти эйлеровы! Можно составить длинный список известных открытий, приоритет в которых принадлежит Эйлеру, и перечень его идей, которые еще заслуживают разработки. Большие математики всегда признавали, что они обязаны Эйлеру многим. «Читайте Эйлера,— обычно говорил молодым математикам Лаплас, – читайте Эйлера, это наш общий учитель». А Гаусс выразился еще более определенно: «Изучение работ Эйлера остается наилучшей школой в различных областях математики, и ничто другое не может это заменить». Риман хорошо знал труды Эйлера, и некоторые из наиболее глубоких его произведений обнаруживают влияние Эйлера. Самым лучшим делом было бы издать переводы некоторых трудов Эйлера с современными комментариями.
5. Поучительно указать не только на то, что Эйлер внес в науку, но и на некоторые его слабости. В восемнадцатом столетии еще достаточно беззаботно обращались с бесконечными процессами и многое в трудах ведущих математиков этого периода производит на нас впечатление безудержного и восторженного экспериментирования. Экспериментировали с бесконечными рядами, с бесконечными произведениями, с интегрированием, с использованием таких символов, как 
. Если многие из выводов Эйлера можно принять сегодня, то есть другие результаты, относительно которых надо делать оговорки. Например, мы принимаем утверждение Эйлера, что 
имеет бесконечно много значений, которые все являются комплексными числами, за исключением того случая, когда 
, тогда одно из значений действительно. Эйлер пришел к этому выводу в письме к Даламберу (1747 г.), который утверждал, что 
. Но мы не можем согласиться с Эйлером, когда он пишет, что 
, или когда он из того, что
и
,
заключает, что
.
Все же нам надо соблюдать осторожность и не критиковать слишком поспешно Эйлера за его обращение с расходящимися рядами: он попросту не всегда пользовался некоторыми из наших нынешних признаков сходимости или расходимости как критериями законности своих рядов. Многое в его считавшихся необоснованных работах о рядах было строго истолковано современными математиками.
Однако мы не можем восторгаться тем способом, которым Эйлер обосновывает анализ, вводя нули различных порядков. Бесконечно малая величина, писал Эйлер в «Дифференциальном исчислении» (1755 г.), – это действительно нуль
.
«Стало быть, существует бесконечно много порядков бесконечно малых величин, и хотя все эти величины равны нулю, следует четко отличать их друг от друга, если мы обращаемся к их взаимозависимости, выражающейся геометрическим отношением».
В целом вопрос об основании анализа оставался предметом обсуждения, равно как и все вопросы, относившиеся к бесконечным процессам. «Мистический период» в обосновании анализа (мы пользуемся термином, предложенным Карлом Марксом) в свою очередь порождал мистицизм, заходивший гораздо дальше того, что мы находим у основателей анализа. Гвидо Гранди, монах и профессор в Пизе, известный своим исследованием лепестковых кривых и других кривых, напоминающих цветки, рассматривал формулу
следовательно 
, как символ творения из ничего. Он получил результат 
, применив такое истолкование: отец завещает драгоценный камень двум своим сыновьям с тем, что каждый может пользоваться драгоценностью поочередно один год; следовательно, камень принадлежит каждому сыну наполовину.
Пусть эйлерово обоснование анализа имело свои слабые стороны, но свою точку зрения Эйлер во всяком случае высказал вполне определенно. Даламбер в некоторых статьях «Энциклопедии» пытался дать такое обоснование другими средствами. Ньютон пользовался выражением «первое и последнее отношение» для «флюксии», имея в виду первое или последнее отношения двух только что возникших величин. Даламбер заменил это понятием предела: Он называет одну величину пределом другой, если вторая, приближаясь к первой, отличается от нее менее чем на любую заданную величину. «Дифференцирование уравнений состоит попросту в том, что находят пределы отношения конечных разностей двух переменных, входящих в уравнение». Это было, наряду с идеями Даламбера о бесконечных различных порядков, значительным шагом вперед. Однако его современников было не так легко убедить в важности этого шага, и когда Даламбер говорил, что секущая становится касательной при слиянии двух точек пересечения в одну, чувствовалось, что он не преодолел трудностей, присущих парадоксам Зенона. В конце концов, достигает ли переменная величина своего предела, или она никогда его не достигает?
Мы уже упоминали о критике ньютоновских флюксий епископом Беркли. Джордж Беркли, первый настоятель в Дерри, после 1734 г. – епископ в Южной Ирландии, а с 1729 до 1731 г. пребывавший в Ньюпорте, штат Род Айленд, прежде всего известен как крайний идеалист («быть – значит восприниматься»). Он был огорчен тем, что ньютонова наука поддерживает материализм, и он напал на теорию флюксий в своем «Аналисте» (Analyst, 1734 г.). Он издевался над бесконечно малыми как над «тенями усопших величин»; если 
получает приращение 
, то приращение 
, разделенное на , есть
Это получается в предположении, что отлично от нуля. Однако флюксию от , то есть 
, получают, считая равным нулю, что сразу изменяет исходное предположение об отличии от нуля. Это было «явным софизмом», который Беркли открыл в анализе, и он был убежден, что верные результаты анализа получаются за счет компенсации ошибок. Логически флюксии нельзя принимать во внимание. «Но тот, кто может переварить вторую или третью флюксию, вторую или третью разность, – восклицал Беркли, обращаясь к неверующему математику (Галлею), – не должен, как мне кажется, придираться к чему-либо в богословии». Это не единственный случай, когда серьезные трудности в науке использовались, чтобы поддержать идеалистическую философию.
Джон Ланден, английский математик-самоучка, чье имя осталось в теории эллиптических интегралов, пытался найти свой метод для преодоления основных затруднений анализа. В своем «Анализе остатков» (Residual analysis, 1764 г.) он ответил на критику Беркли тем, что полностью избегал бесконечно малых; например, производную от 
он находил, заменяя на 
, после чего
становится равным 
, когда 
. Так как этот метод приводит при более сложных функциях к бесконечным рядам, он находится в известном родстве с более поздним алгебраическим методом Лагранжа.
5*. Для России, с которой Эйлер был связан в течение почти всей своей научной деятельности (в годы жизни в Берлине он оставался деятельным сочленом Петербургской академии, печатая в ее изданиях значительную часть своих работ, консультируя по различным вопросам, включая подбор сотрудников Академии, и руководя занятиями командированных к нему молодых ученых), его труды имели особое значение. Многие прикладные работы Эйлера, например по картографии и по морскому делу, были предприняты, чтобы дать ответ на запросы русских правительственных учреждений. В России печатались и трактаты Эйлера, и его учебники элементарного содержания, значительно повысившие уровень математического просвещения: «Руководство к арифметике» Эйлера вышло на русском языке двумя изданиями (1740 и 1760 гг.), «Универсальная арифметика» по-русски была издана раньше (1768–1769 гг.), чем ее немецкий оригинал, «Полное введение в алгебру» (1770 г.), и выдержала три издания. У Эйлера учились первые русские академики по математике (С К. Котельников, 1723–1806) и по астрономии (С. Я. Румовский, 1734–1812, известный также и как автор нескольких математических работ). Во второй петербургский период Эйлер становится центром целой группы ученых, в которую входят, кроме названных: его сын, И.А. Эйлер, чьи заслуги, впрочем, сводятся к тому, что он был «техническим» помощником отца; племянник Эйлера Н.И. Фусс (1755–1826), тоже помогавший почти слепому Эйлеру, автор многих оригинальных исследований, преимущественно по дифференциальной геометрии; А.И. Лекселль (1740–1781), известный своими работами по полигонометрии; астроном и геометр Ф.И. Шуберт (1758–1828). Самостоятельные математические исследования этих учеников Эйлера, состоят преимущественно в решении частных задач, поставленных в работах учителя или связанных с ними, притом с определенным геометрическим уклоном и в рамках эйлеровых методов и приемов. Такое направление вело в сторону от столбовой дороги математики того времени, и в девятнадцатом веке потребовались труды М.В. Остроградского и П.Л. Чебышева, чтобы придать новый блеск Петербургской математической школе.
6. Хотя Эйлер неоспоримо был ведущим математиком этого периода, во Франции по-прежнему появлялись вполне оригинальные работы. Здесь более чем в какой-либо другой стране математику рассматривали как науку, которая должна была довести теорию Ньютона до большего совершенства. Теория всемирного тяготения обладала большой привлекательностью в глазах философов Просвещения, которые пользовались ею как оружием в своей борьбе против остатков феодализма. Католическая церковь включила труды Декарта в индекс запрещенных книг 1664 г., но около 1700 г. его теории стали модными даже в консервативных кругах. Проблема: ньютонианство или картезианство – стала на некоторое время наиболее интересной темой не только для ученых, но и в салонах. «Письма об англичанах» (1734 г.) Вольтера много сделали для знакомства французских читателей с идеями Ньютона; подруга Вольтера мадам Дю Шатле даже перевела «Начала» на французский язык (1759 г.). Существенно спорным вопросом для обеих школ был вопрос о форме Земли.
Согласно космогонии, которую поддерживали картезианцы, Земля у полюсов была удлинена, а по теории Ньютона она должна была там быть сплющена. Картезианские астрономы Кассини (отец Шан Доминик и сын Жак; отец известен в геометрии благодаря овалам Кассини, 1680 г.) промерили дугу меридиана во Франции между 1700 и 1720 гг. и отстаивали картезианский вывод. Возник спор, в котором приняли участие многие математики. В 1735 г. в Перу послали экспедицию, за которой в 1736–1737 гг. последовала другая экспедиция в Лапландию, под руководством Пьера Мопертюи, с целью промерить градус долготы. В результате обеих экспедиций восторжествовала теория Ньютона, это было как ее триумфом, так и триумфом самого Мопертюи. Отныне знаменитый «Великий сплющиватель» стал президентом Берлинской академии и много лет купался в лучах своей славы при дворе Фридриха II. Это продолжалось до 1750 г., когда он вступил в горячий спор со швейцарским математиком Самуилом Кёнигом относительно принципа наименьшего действия в механике, указанного, быть может, уже Лейбницем. Мопертюи, как Ферма до него и Эйнштейн после него, искал какой-то общий принцип, который мог бы объединить законы вселенной. Формулировка Мопертюи не была отчетливой, он определял свое «действие» как величину 
(
– масса, 
– скорость, 
– расстояние). У него это сочеталось с доказательством существования бога. Этот спор особенно обострился тогда, когда Вольтер высмеял неудачливого президента в своей «Диатрибе доктора Акакия, врача папы» (1752 г.). Ни поддержка короля, ни защита Эйлера не могли уже вернуть Мопертюи присутствие духа, и павший духом математик вскоре скончался в Базеле, в доме Бернулли.
Эйлер вновь выдвинул принцип наименьшего действия в формулировке, что должен быть минимумом 
, и, кроме того, он не вдавался в метафизику Мопертюи. Таким образом, этот принцип был поставлен на твердую почву, и им пользовался Лагранж, позже – Гамильтон. Значение «гамильтониана» в современной математической физике показывает, насколько существенным было то, что внес Эйлер в спор между Мопертюи и Кёнигом.
Среди математиков, побывавших вместе с Мопертюи в Лапландии, был Алексис Клод Клеро. Клеро восемнадцати лет от роду опубликовал «Изыскания о кривых двоякой кривизны» (Recherches sur les courbes a double courbure), первый опыт в области аналитической и дифференциальной геометрии пространственных кривых. По возвращении из Лапландии Клеро опубликовал свою «Теорию фигуры Земли» (Theorie de la figure de la Terre, 1743 г.), образцовое произведение no гидростатике и притяжению эллипсоидов вращения. Лаплас мог его улучшить лишь в незначительных деталях. В числе главных результатов этой работы – условие полноты дифференциала 
. За этой книгой последовала «Теория Луны» (Theorie de la lune, 1752 г.), содержавшая дополнения к эйлеровой теории движения Луны и к общей задаче трех тел. Клеро принадлежат также результаты в теории криволинейных интегралов и дифференциальных уравнений. Один из типов рассмотренных им дифференциальных уравнений известен под его именем, и с этим связан один из первых примеров особых решений.
7. Интеллектуальная оппозиция старому режиму после 1750 г. имела своим центром знаменитую «Энциклопедию» (1751–1772 гг., 28 томов). Ее редактором был Дени Дидро, под чьим руководством «Энциклопедия» стала подробным изложением философии века Просвещения. Дидро не обладал большими познаниями в математике, ведущим математиком энциклопедистов был Жан ле Рон Даламбер, внебрачный сын аристократической дамы, оставленный как подкидыш вблизи церкви святого Жана ле Рона в Париже. Его ранние и блестящие успехи облегчили его карьеру. В 1754 г. он стал «непременным секретарем» Французской академии и в качестве такового наиболее влиятельным ученым Франции. В 1743 г. появился его «Трактат по динамике» (Traite de la dynamique), который содержит метод сведения динамики твердых тел к статике, известный как «принцип Даламбера». Он продолжал писать по многим прикладным вопросам, в частности по гидродинамике, аэродинамике и задаче трех тел. В 1747 г. он опубликовал теорию колебания струн, что делает его, вместе с Даниилом Бернулли, основателем теории уравнений в частных производных. Тогда как Даламбер и Эйлер нашли решение уравнения 
в виде 
, Бернулли решил это уравнение при помощи тригонометрических рядов. Возникли серьезные сомнения относительно характера этого решения: Даламбер считал, что начальная форма струны может быть задана только одним-единственным аналитическим выражением, в то время как Эйлер полагал, что допустима любая непрерывная кривая. Бернулли утверждал, вопреки Эйлеру, что его решение в виде ряда является вполне общим. Полного разъяснения этого вопроса придаюсь ждать до 1814 г., когда Фурье устранил сомнения относительно законности представления «любой» функции тригонометрическим рядом.
Даламберу не составляло труда писать по многим вопросам, включая даже вопросы обоснования математики. Мы упоминали о том, что он ввел понятие предела. «Основную теорему алгебры» иной раз называют теоремой Даламбера, так как он пытался ее доказать (1746 г.), а «парадокс Даламбера» в теории вероятностей показывает, что он, хотя и не очень успешно, размышлял об основах этой теории.
Теория вероятностей быстро развивалась в течение этого периода главным образом благодаря дальнейшей разработке идей Ферма, Паскаля и Гюйгенса. За «Ars conjectandi» последовали другие книги, среди них «Учение о случае» (The Doctrine of Chance, 1716 г.), написанная Авраамом де Муавром, французским гугенотом, который поселился в Лондоне после отмены Нантского эдикта (1685 г.) и зарабатывал там на жизнь частными уроками. Имя де Муавра связано с тригонометрической теоремой, которая в ее современной форме 
впервые появляется во «Введении» Эйлера. В 1733 г. Муавр вывел функцию нормального распределения как аппроксимацию биномиального закона и дал формулу, равносильную формуле Стирлинга. Джеймс Стирлинг, английский математик школы Ньютона, опубликовал свой ряд в 1730 г.
Многочисленные лотереи и страховые компании, которые организовались в течение этого периода, вызвали у многих математиков, включая Эйлера, интерес к теории вероятностей. Это повело к попыткам применить учение о вероятностях в новых областях. Бюффон, известный как автор «Естественной истории» (36 увлекательно написанных томов) и знаменитого рассуждения о стиле (1753 г.; «стиль – это человек»), в 1777 г. дал первый пример геометрической вероятности. Это была так называемая задача об игле, которая занимала многих, так как она давала возможность экспериментально определить число 
, бросая иголку на плоскость, покрытую параллельными и равноудаленными прямыми, и подсчитывая число пересечений иголки с этими прямыми.
К этому периоду относятся также попытки применить теорию вероятностей к суждениям человека; например, подсчитывали шансы на то, что какой-либо трибунал сможет вынести правильный приговор, если для каждого из свидетелей можно указать число, выражающее вероятность того, что он будет говорить правду. Эта забавная «вероятность суждений», которая отдает философией века Просвещения, занимает видное место в трудах маркиза Кондорсе; она появляется еще у Лапласа и даже у Пуассона (1837 г.).
8. Де Муавр, Стирлинг и Ланден – добротные представители английской математики восемнадцатого века. Но мы должны сказать и о некоторых других англичанах, хотя никто из них не мог равняться со своими коллегами на континенте. Над английской наукой тяготела традиция почитания Ньютона, и его обозначения, неуклюжие по сравнению с обозначениями Лейбница, затрудняли прогресс. Были и глубокие общественные причины, в силу которых английские математики не освобождались от флюксионных методов Ньютона. В Англии, которая вела непрерывную торговую войну с Францией, развивалось чувство интеллектуального превосходства, которое поддерживалось не только победами, военными и торговыми, но тем восхищением, которое вызывала у континентальных философов английская политическая система. Англия стала жертвой своего воображаемого совершенства. Есть сходство между английской математикой восемнадцатого века и античной математикой позднеалександрийской эпохи. В обоих случаях неподходящие обозначения технически затрудняли прогресс, а причины того, что математики ими удовлетворялись, были более глубокого общественного характера.
Ведущим английским, вернее пользовавшимся английским языком, математиком этого периода был Колин Маклорен, профессор Эдинбургского университета, последователь Ньютона, с которым он был лично знаком. Его исследования и обобщения флюксионного метода, работы по кривым второго и более высокого порядка и по притяжению эллипсоидов шли параллельно с исследованиями Клеро и Эйлера. Некоторые из теорем Маклорена вошли в нашу теорию плоских кривых и в нашу проективную геометрию. В его «Органической геометрии» (Geometria organica, 1720 г.) мы находим замечание, известное как парадокс Крамера: кривая 
-го порядка не всегда определяется 
точками, так что девять точек могут не определять однозначно кривую третьего порядка, тогда как может оказаться, что десяти точек слишком много. Здесь же мы находим кинематические методы для описания плоских кривых различных порядков. «Трактат о флюксиях» Маклорена (Treatise of fluxions, 2 тома, 1742 г.), написанный в защиту Ньютона против Беркли, читать трудно из-за его архаичного геометрического языка, что находится в резком контрасте с доступностью работ Эйлера. Маклорен обычно стремился к строгости Архимеда. В книге содержатся исследования Маклорена о притяжении эллипсоидов вращения и его теорема, что два таких конфокальных эллипсоида притягивают частицу на оси или на экваторе силами, пропорциональными их объемам. В этом трактате Маклорен оперирует также со знаменитым «рядом Маклорена».
Впрочем, этот ряд не был новым открытием, так как он появился в «Методе приращений» (Methodus incrementorum, 1715 г.), написанном Бруком Тейлором, в то время секретарем Королевского общества, а еще раньше был открыт И. Бернулли и, по сути, был известен Лейбницу. Маклорен признает то, что он полностью обязан Тейлору. Ряд Тейлора теперь всегда приводят в обозначениях Лагранжа:
Тейлор явно приводит этот ряд для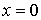 
, что многие учебники еще упорно называют рядом Маклорена. В выводе Тейлора нет соображений относительно сходимости ряда, но Маклорен положил начало таким исследованиям и даже владел так называемым интегральным признаком сходимости бесконечных рядов. Полностью важность ряда Тейлора была признана лишь после того, как Эйлер использовал его в своем «Дифференциальном исчислении» (1755 г.). Лагранж добавил к нему остаточный член и положил его в основу своей теории функций. Сам Тейлор использовал свой ряд для интегрирования некоторых дифференциальных уравнений. Он начал исследование колебаний струны, что затем было предметом работ Даламбера и др.
9. Жозеф Луи Лагранж родился в Турине в итало-французской семье. Девятнадцати лет от роду он стал профессором математики артиллерийской школы в Турине (1755 г.). В 1766 г., когда Эйлер уехал из Берлина в Петербург, Фридрих II пригласил Лагранжа в Берлин, и в этом скромном приглашении было сказано, что «необходимо, чтобы величайший геометр Европы проживал вблизи величайшего из королей». Лагранж оставался в Берлине до смерти Фридриха (1786 г.), после чего он переехал в Париж. Во время революции он участвовал в реформе мер и весов, а позже стал профессором сначала Нормальной школы (1795 г.), а затем Политехнической школы (1797 г.).
Исследования по вариационному исчислению относятся к раннему периоду деятельности Лагранжа. Мемуары Эйлера по этому вопросу появились в 1755 г. Лагранж заметил, что метод Эйлера не обладает «