Основные теоретические сведения к задаче №2

Расчет индуктора для электросушки железобетонных изделий

Условие задачи

Для обеспечения индуктивного нагрева малогабаритных железобетонных изделий сложной конфигурации применяется индуктор в виде катушки индуктивности без сердечника, выполненной из провода с электрическим сопротивлением R. При включении индуктора в сеть переменного тока с частотой f = 50 Гц и действующим значением напряжения U ток в катушке имеет действующее значение I ₁. Исходные данные для 30 вариантов приведены таблице 1.2.

Таблица 1.2

Номер варианта	Напряжение сети	Ток катушки	Активное сопротивление катушки	Емкостное сопротивление конденсатора
U, B	I 1, А	R, Ом	XC, Ом
			0,6	1,8
			0,8	2,4
			1,2	3,6
			1,5	4,5

Часть 1

Требуется:

1.1. Для указанных условий начертить (скопировать) эквивалентную схему замещения катушки индуктивности, включенной на переменное напряжение (см. рис. 1.4,а).

1.2. Определить полное сопротивление катушки Z _K и ее индуктивное сопротивление X _L.

1.3. Рассчитать индуктивность катушки L (в миллигенри – мГн) и коэффициент мощности катушки cos φ₁.

1.4. Рассчитать падения напряжений U _R и U_L на активном R и индуктивном X _L сопротивлениях катушки.

1.5. Определить активную мощность P ₁, реактивную индуктивную мощность Q ₁ и полную мощность S ₁ катушки индуктивности.

1.6. Для катушки индуктивности построить в масштабе векторную диаграмму с указанием фазового угла φ₁.

Часть 2.

Для изменения энергетических характеристик индуктора параллельно его обмотке подключают конденсатор С с емкостным сопротивлением Х_С.

Требуется:

2.1. Начертить (скопировать) электрическую схему включения катушки параллельно конденсатору (рис. 1.4,б).

2.2. Определить ток I_C протекающий по конденсатору.

2.3. Рассчитать ток I ₂, потребляемый этой цепью и коэффициент мощности цепи cos φ₂.

2.4. Определить относительное уменьшение тока, потребляемого цепью I ₂ /I ₁ при включении конденсатора.

2.5. Определить активную Р ₂, реактивную Q ₁ и полную S ₁ мощности этой цепи.

2.6. Построить в масштабе векторную диаграмму и треугольник мощностей для данной цепи, совмещенный с треугольником мощностей для случая катушки без конденсатора.

2.7. Ответить письменно на вопросы:

- Как влияет на коэффициент мощности цепи параллельное подключение конденсатора к индуктивной нагрузке?

- Зачем необходимо повышать коэффициент мощности электроустановки, имеющей активно-индуктивный характер нагрузки?

Часть 3.

Обмотку индуктора и конденсатор соединяют последовательно.

Требуется:

3.1. Начертить (скопировать) электрическую схему последовательного соединения катушки индуктивности и конденсатора (см. рис. 1.4,в).

3.2. Определить полное сопротивление Z ₃ и ток I ₃ в цепи.

3.3. Рассчитать падения напряжения U ' _R, U ' _L, U ' _C на участках цепи.

3.4. Построить в масштабе векторную диаграмму для данной цепи.

а)	б)	в)

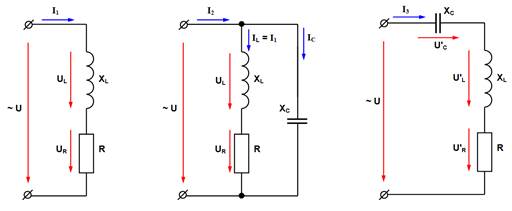
Рис. 1.4. Эквивалентные схемы замещения к задаче №2

а) катушка индуктивности (индуктор);
б) катушка индуктивности с параллельно включенным конденсатором;
в) катушка индуктивности с последовательно включенным конденсатором

Основные теоретические сведения к задаче №2

Индуктивный нагрев железобетонных изделий осуществляется благодаря тому, что магнитное поле индуктора (катушки индуктивности) наводит в проводящих элементах (арматуре) и слоях бетона с ионной проводимостью электродвижущие силы (ЭДС), вызывающие прохождение в этих элементах и слоях вихревых (индукционных) токов. Циркуляция токов с частотой f создает омические (тепловые) потери и выделение тепла, разогревающего изделие по всей его массе. При нагреве влажного железобетонного изделия интенсифицируется процесс его сушки.

Схема замещения катушки представлена на рис. 1.4,а. Катушка обладает индуктивностью L с индуктивным сопротивлением X_L и активным сопротивлением провода катушки R.

Активное сопротивление катушки R – это внутреннее электрическое сопротивлению провода катушки, равное сопротивлению постоянному току, то есть оно не зависит от частоты проходящего через катушку тока.

Индуктивное сопротивление X_L пропорционально частоте f тока катушки и ее индуктивности L:

,

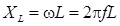где f – частота сети, равная 50 Гц; w – угловая частота тока, рад/с.

Из этой формулы видно, как можно определить индуктивность L катушки по заданному индуктивному сопротивлению X_L.

Внимание! Результат расчета индуктивности следует записать в миллигенри (10^–3 Гн).

Индуктивность катушки является мерой ее электромагнитной инерции и зависит от конфигурации, размеров, числа витков катушки, а также от наличия или отсутствия в катушке магнитопровода [1].

Полное сопротивление катушки индуктивности Z_K может быть определено в соответствии с законом Ома:

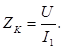
Полное сопротивление катушки Z_K, состоящее из активного сопротивления R и индуктивного сопротивления X_L можно записать в виде

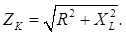
Из этой формулы видно, что полное сопротивление Z_K, активное сопротивление R и индуктивное сопротивление X_L катушки индуктивности составляют соответственно гипотенузу и катеты прямоугольного треугольника. Этот прямоугольный треугольник называется треугольником сопротивлений [1.3].

Наличие индуктивности вызывает некоторое отставание (сдвиг) фазы тока по отношению к фазе напряжения на угол φ ₁, в чем и проявляется упомянутая электромагнитная инерция катушки.

Природа индуктивного сопротивления катушки связана с созданием вокруг нее переменного магнитного поля. Это поле в соответствии с законом электромагнитной индукции наводит в витках катушки ЭДС самоиндукции, знак которой в каждый момент времени противоположен знаку приложенного к катушке напряжения. В каждый момент времени ЭДС препятствует как нарастанию тока в катушке, так и его уменьшению.

Следовательно, чем больше частота тока (т.е. скорость его изменения), тем больше противодействие его изменению и прохождению, т. е. тем больше индуктивное сопротивление катушки X_L.

Угол сдвига между мгновенными значениями напряжения и тока, либо между векторами напряжения U и тока I ₁ обозначается φ, а cos φ называется коэффициентом мощности.

Поскольку первопричиной отставания тока от напряжения является индуктивный характер сопротивления, то и угол между полным сопротивлением катушки Z_K и индуктивным сопротивлением X_L втреугольнике сопротивлений будет также равен φ ₁. Откуда:

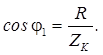
Катушка (индуктор) потребляет активную Р ₁и реактивную Q ₁ мощности. Мощность Р ₁ соответствует потерям активной мощности в витках катушки, обладающей активным сопротивлением провода R при прохождении через катушку тока I ₁:

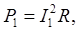Вт,

или

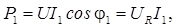
где U_R – падение напряжения на активном сопротивлении катушки.

Реактивная мощность Q ₁ = Q_L идет на создание магнитного поля катушки:

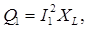Вар,

или

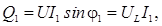
где U_L – падение напряжения на индуктивном сопротивлении катушки.

Полная мощность S ₁ катушки индуктивности:

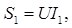ВА,z:\CorvDoc\lektsiiorg1-\Equation.DSMT4

или

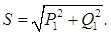
Из этой формулы видно, что полная S ₁ активная Р ₁ и реактивная Q ₁ мощности катушки геометрически соотносятся как гипотенуза и катеты прямоугольного треугольника, который называется треугольником мощностей, причем угол φ заключен между гипотенузой S ₁ и катетом Р ₁.

Величина коэффициента мощности

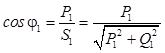
показывает, какую долю от потребляемой полной мощности S ₁ занимает активная мощность Р ₁. Поэтому величина cos φ₁ является коэффициентом мощности катушки. Наряду с коэффициентом полезного действия, коэффициент мощности является важнейшим энергетическим показателем электроприемника с активно-индуктивным характером нагрузки [1,3].

Электрические величины – синусоидальные напряжения, ЭДС, токи для удобства анализа физических процессов представляют в виде комплексных или векторных величин, характеризуемых, как известно [1], направлением и модулем. Например, действующее значение синусоидального напряжения

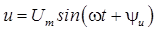
можно записать в виде комплексного числа в трех формах: алгебраической

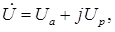
тригонометрической

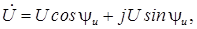
показательной

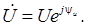
Здесь

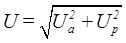– модуль комплекса напряжения, равный длине вектора этой величины, который определяет действующие значение соответствующего напряжения; y _u = arctgU_р/U_а – аргумент комплекса напряжения, равный его начальной фазе; 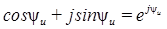– формула Эйлера, связывающая алгебраическую и показательную формы записи комплексных чисел; е – основание натурального логорифма; 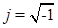– мнимая единица.

Таким образом, комплексное число или просто комплекс тока или напряжения в любой из выше перечисленных форм записи является отображением соответствующей синусоидальной функции тока или напряжения.

Совокупность векторов комплексных значений синусоидальных величин одной частоты, показывающая их взаимное расположение, называют векторной диаграммой. Удобство использования векторных диаграмм состоит в том, что сложение и вычитание комплексных значений можно заменить геометрическим сложением и вычитанием непосредственно векторов.

Векторная диаграмма строится в комплексной плоскости. Для удобства анализа первый вектор, направляют вдоль оси действительных величин. Дальнейшие построения диаграммы осуществляют относительно этого вектора (тока или напряжения), который называют исходным, опорным или базовымвектором. Подробные правила построения векторных диаграмм изложены в [3].

В первой части задачи для построения векторной диаграммы катушки (см. п. 1.6 задания) вначале следует определить, в соответствии с законом Ома, падение напряжения на активном U_R и индуктивном U_L сопротивлениях катушки и выбрать подходящий масштаб напряжения (М_U, В/см).

При этом вектор тока катушки I ₁ (определенный в предварительно выбранном масштабе М_I, A/см) откладывается вдоль оси действительных величин (горизонтально вправо) и является базовым вектором.

В электротехнике принято считать направление вращения векторов против часовой стрелки положительным, а в обратную сторону (по часовой стрелке) – отрицательным. Следовательно, вектор, сдвинутый против часовой стрелки на фазовый угол φ относительно базового, будет вращаться по отношению к нему с опережением и называться опережающим вектором, а сдвинутый по часовой стрелке относительно базового – отстающим вектором [3].

Во второй части задачи говорится о том, что для изменения энергетических характеристик индуктора параллельно его обмотке подключают конденсатор С, обладающий емкостным сопротивлением Х_С (см. рис. 1.4,б).

Подключение конденсатора емкостью С существенно изменяет электромагнитные процессы в цепи, поскольку природа емкостного сопротивления Х_С отличается от индуктивного сопротивления Х_L.

Емкостное сопротивление связано с созданием электрического поля между обкладками конденсатора. При этом ток цепи внутри конденсатора представляет собой ток смещения, обеспечивающий разделение электрических зарядов диэлектрика конденсатора и выделения их на обкладках конденсатора, т.е. образованию электрического поля [1].

В случае индуктивности мгновенное значение мощности изменяется периодически с двойной частотой сети: катушка дважды успевает накопить энергию магнитного поля и вернуть ее в сеть. В конденсаторе процесс накопления энергии электрического поля и возврат ее в сеть также происходит с двойной частотой, однако при этом емкость отдает в сеть энергию в то самое время, когда индуктивность получает ее из сети и наоборот. Следовательно, в каждый момент времени синусоидальные токи конденсатора С и катушки индуктивности L находятся в противофазе (угол сдвига по фазе равен π), а векторы этих токов имеют противоположные направления. Это физическое явление имеет чрезвычайно важное практическое значение.

В системе электроснабжения, имеющей электроприемники с индуктивным характером нагрузки (индукционные печи, асинхронные двигатели и др.) параллельно к ним подключают конденсаторные батареи (косинусные конденсаторные установки). Эти установки компенсируют значительную часть реактивной (индуктивной) мощности, потребляемой электроприемником с индуктивным характером нагрузки, благодаря чему провода и кабели энергосистемы разгружаются от реактивной составляющей тока, а также уменьшаются потери энергии в них [1,3].

Когда конденсатор С подключается параллельно катушке к напряжению U, через него протекает ток I_C, который определяется на основании закона Ома через U и Х_С.

Ток I ₂, потребляемый цепью с параллельно включенной катушкой индуктивности и конденсатором можно определить на основании векторной диаграммы для этой цепи (см. рис. 1.5).

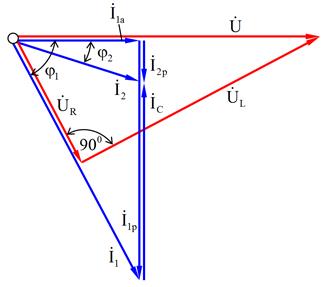
Рис. 1.5. Векторная диаграмма цепи с параллельно включенной катушкой индуктивности и конденсатором (часть 2 задачи №2)

Из векторной диаграммы видно, что ток I ₁, протекающий через катушку (см. рис. 1.4,б) имеет активную I _1а и реактивную I _1р составляющие, которые определяются из тригонометрических формул

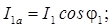
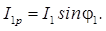
Вектор общего реактивного тока цепи 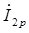равен геометрической сумме токов 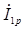и :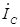

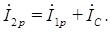
В то же время величина реактивной составляющей тока, потребляемого цепью I _{2 р} определяется величиной разности разнонаправленных токов I _{1 р} катушки и тока I_С конденсатора С:

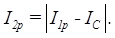
Из векторной диаграммы видно, что величина тока I₂, потребляемого этой цепью определяется с помощью формулы теоремы Пифагора, как

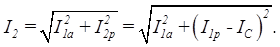
Коэффициент мощности цепи с параллельно включенной катушкой и конденсатором определяется из прямоугольного треугольника токов I_1а, I_2р, I₂ по формуле

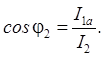
Векторную диаграмму для цепи с параллельно соединенными катушкой и конденсатором (см. рис. 1.5) следует начать с построения в выбранном масштабе для напряжений (M_U, В/см) базового вектора U. Затем следует в том же масштабе отложить векторы активной I _{1 а} и реактивной I _{1 р} составляющий тока катушки. Далее строится вектор емкостного тока I_С, начало которого совпадает с концом тока I _{1 р} , и направленный противоположно току I _{1 р} . Величина вектора реактивной составляющей тока, потребляемого цепью I _{2 р} , как было выше сказано, определяется величиной разности разнонаправленных токов I _{1 р} катушки и тока I_С конденсатора. Вектор тока I ₂, потребляемого этой цепью откладывается как гипотенуза прямоугольного треугольника на катетах-векторах токов I _{1 а} и I _{2 р} . Вектор напряжения на активном сопротивлении U_R совпадает с вектором тока катушки I ₁, а вектор падения напряжения на индуктивном сопротивлении U_L опережает этот ток на фазовый угол 90⁰. На построенной векторной диаграмме следует отложить фазовые углы φ ₁ и φ ₂ как показано на рис. 1.5.

Из векторной диаграммы рис. 1.5 следует, что компенсация реактивной составляющей тока катушки индуктивности I _{1 р} током конденсатора I_С приводит к уменьшению величины реактивной составляющей тока I _{2 р} , потребляемого этой цепью и, следовательно, самого тока I ₂. Показателем этого уменьшения служит коэффициент мощности цепи cosφ ₂. Видно, что при уменьшении фазового угла φ ₂ до нуля cosφ ₂ становится равным единице, индуктивный ток катушки I _{1 р} полностью компенсируется емкостным током конденсатора I_С. При этом общий реактивный ток цепи I _{2 р} снижается до нуля, а потребляемый цепью ток I ₂ становится минимально возможным и равным активной составляющей тока катушки, определяемый формулой

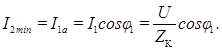
Одновременно с уменьшением потребляемого цепью тока (с величины I₁ до I₂) при включении конденсатора происходит компенсация реактивной индуктивной мощности катушки Q ₁ реактивной емкостной мощностью конденсатора Q_С. Поэтому общая реактивная мощность Q ₂ цепи с конденсатором 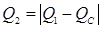становится меньше.

При параллельном подключении к катушке конденсатора также происходит уменьшение полной мощности, поскольку она изменяется пропорционально току:

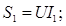
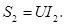
Внимание! Активная мощность, потребляемая цепью при включении конденсатора, остается постоянной, так как при этом не изменяется ток катушки 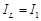(см. рис. 1.4,а и рис. 1.4,б):

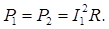
Поэтому прямоугольный треугольник мощностей для данной цепи, совмещенный с треугольником мощностей для случая катушки без конденсатора строится на одном общем горизонтальном катете, соответствующем активной мощности катушки.

На совмещенном треугольнике мощностей следует обозначить фазовые углы φ₁ и φ₂ для обеих цепей.

В третьей части задачи вначале следует определить полное сопротивление Z ₃ и ток I ₃, а также падения напряжения U'_R, U'_L, U'_C на участках цепи в цепи с последовательно соединенными R, L, C -элементами (см. рис. 1.4,в), пользуясь пояснениями, изложенными в [3].

Рекомендуется просмотреть правила построения векторных диаграмм и теоретический материал к соответствующим лабораторным работам, представленные в [3].

Примечания

1. Правильность решения задачи проверьте с помощью блок-схем алгоритма решения задачи на рис. 1.6 – рис. 1.8.

2. Ответы на вопросы пп. 2.7 задания можно найти, проанализировав теоретические сведения, приведенные в этом разделе и в [1].

 

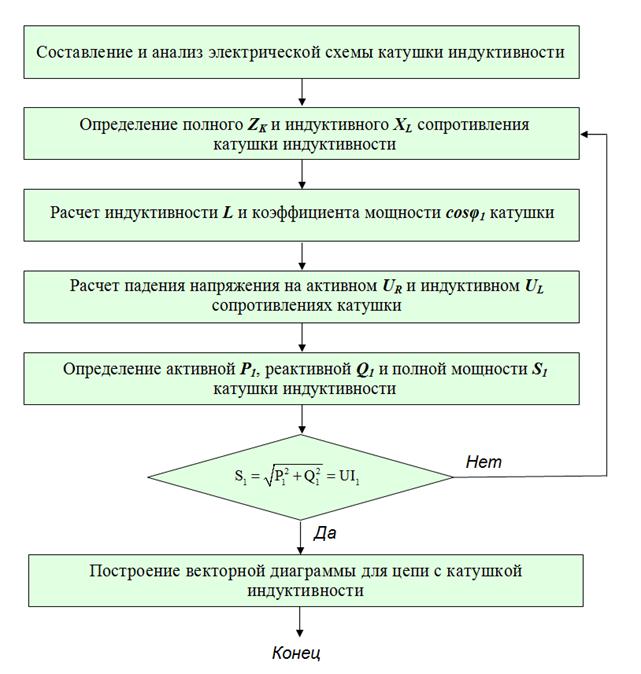
Рис. 1.6. Блок-схема алгоритма к задаче № 2, часть 1

 

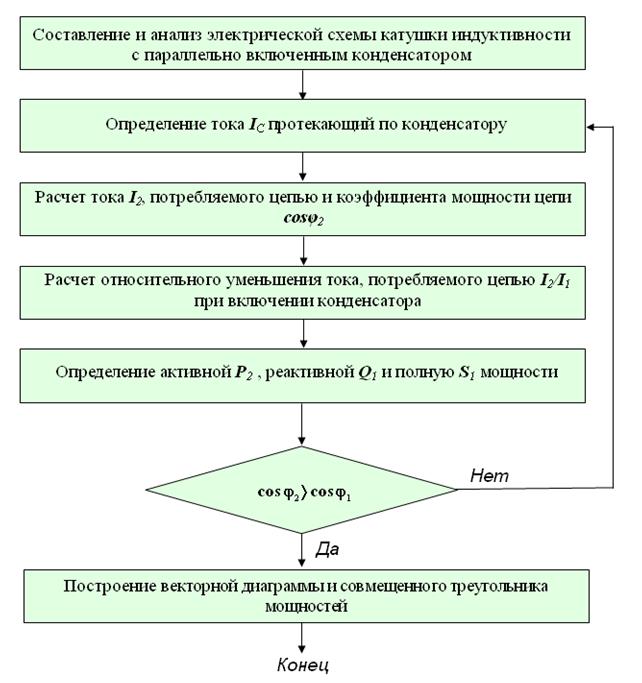
Рис. 1.7. Блок-схема алгоритма к задаче № 2, часть 2

 

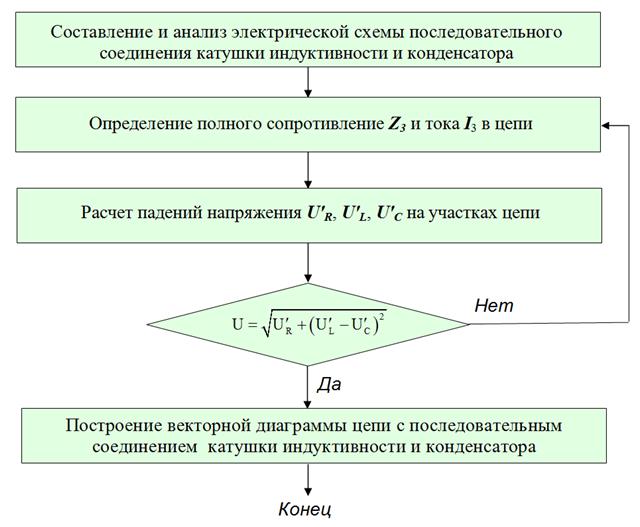
Рис. 1.8. Блок-схема алгоритма к задаче № 2, часть 3