ЗАДАНИЕ № 11. ТЕМА: Статистические методы обработки результатов измерений.

1. Цель: научиться применять статистические методы обработки результатов измерений.

2. Задачи: закрепить умения строить графики распределения частот в вариационном ряду, определять основные статистические характеристики вариационного ряда, определять доверительный интервал для среднего значения генеральной совокупности, выявлять достоверность различия между данными двух выборок одной и той же генеральной совокупности, выявлять корреляционную связь между признаками.

3. Контрольное задание: так как курс математической статистики был пройден ранее курса спортивной метрологии, то по решению преподавателя студенты выполняют одну или две задачи из предлагаемых ниже.

 

Задача 1. Провести тестирование прыжка в длину с места (можно предложить для каждого студента различные тесты) 20 исследуемых. Построить графики вариационного ряда 20 исследуемых по показателям результатов тестирования прыжка в длину с места, если данные полученной выборки таковы:

х_i, см - __________________________________________________________

________________________________________________________________

 

 

Решение:

 

1) произвести ранжирование вариационного ряда в порядке неубывания:

 

х_i. cм - _________________________________________________________

 

 

2) определяем минимальное и максимальное значения вариант и рассчитываем размах вариационного ряда по формуле:

 

R = х_max – х_min R =

 

3) рассчитываем число интервалов по формуле Стерджеса:

k = 1 + 3.32 lg n lg 20 = 1.301

 

k = 1 + 3.32 х 1,301 = 5,31932 ≈ 5

 

4) рассчитываем ширину интервала каждого класса по формуле:

 

h =

 

h=

 

5) составляем таблицу границ классов:

№ класса	Граница класса	Среднее значение класса	Частота класса	Накопленная частота класса
	хmin - £ хi < хmin + £ хi <
	хmin + £ хi < хmin + £ хi <
	хmin + £ хi < хmin + £ хi <
	хmin + £ хi < хmin+ £ хi <
	хmin + £ хi < хmin + £ хi <

 

6) рассчитываем среднее значение каждого класса по формуле:

 

х _ср.зн. =

 

7) построим графики гистограммы и полигона данного вариационного ряда.

y Частота класса

	Результаты, см

Рис. Графическое изображение вариационного ряда.

 

Сделать вывод об однородности группы по заданному признаку, учитывая следующие моменты:

- если гистограмма и полигон по своему виду близки к виду графика нормального распределения величин, то группа однородна;

- если графики низкие и растянутые, то группа, возможно, однородна, но некомпактна;

- если графики имеют 2 и более вершин, то группа неоднородна по данному признаку, ее необходимо разбить на подгруппы, чтобы с каждой из подгрупп вести занятия по индивидуальному плану.

Вывод:

 

 

Задача 2. Определить основные статистические показатели тестирования 10 исследуемых в тесте ____________________, если данные выборки таковы:

х_i - _____________________________________________________________

 

 

Решение:

 

	хi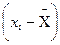

 

 

2.1. Рассчитать значение средней арифметической величины:

 

 

2.2. Рассчитать значение стандартного отклонения:

 

2.3. Рассчитать стандартную ошибку средней арифметической величины:

 

 

2.4. Рассчитать ошибку репрезентативности:

 

 

2.5. Рассчитать коэффициент вариации:

 

 

2.6. Сделать по результатам вывод о компактности группы по заданному признаку, учитывая, что:

- чем больше коэффициент вариации (V), тем более изменчив признак;

- значение коэффициента вариации, не выходящие за пределы 10%, принято считать нормальными;

- если V > 20%, то выборка не компактна по заданному признаку.

 

 

Задача 3. Определить доверительный интервал пульса покоя за 1 мин с уверенностью b=95% у спортсменов (вид спорта)_________, если данные выборки таковы:

Х, уд - ____________________________________________________ (n=10)

 

Решение:

 

1) доверительный интервал по Стьюденту имеет вид:

 

 

где: - среднее значение генеральной совокупности;

- ошибка среднего арифметического, вычисляемая по формуле:

 

где t – число Стьюдента из таблицы;

- уровень доверительной вероятности.

 

2) занести результаты тестирования в рабочую таблицу и произвести необходимые расчеты:

 

	хi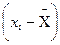

 

s =

 

m_x =

 

 

3) Число степеней свободы k=n

Тогда при k=10 и

Отсюда

 

£ £

 

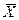Cделать по результатам вычислений вывод.

Вывод: с уверенностью b= 95% можно утверждать, что среднее значение генеральной совокупности показателя пульса покоя за 1 минуту не вышло бы за пределы от _____ до ____ ударов.

 

 

Задача 4. Определить достоверность различия двух групп студентов по средним арифметическим, если по числу подтягиваний эти группы показали следующие результаты:

 

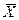=10,0 n_x=35 =±1.3

 

=14.5 n_y=40 =±1.5

 

Решение:

 

Задача на случай, когда группы большие по объему и варианты попарно-независимы. Следовательно, решать следует по формулам:

 

 

По таблице t-критериев Стьюдента определим доверительную вероятность:…..<b<…… Итак, различие не случайно (случайно). Оно достоверно по ….порогу доверительной вероятности или не достоверно.

 

Задача 5. Сравнить какая группа студентов по показателю ЧСС покоя лучше, если их результаты таковы (х_i – данные 1- й группы, y_i – данные 2-й группы):

 

х_i,уд/мин _______________________________________________________

 

y_i,,уд/мин _______________________________________________________

 

Решение:

 

1) результаты тестирования занести в рабочую таблицу и выполнить соответствующие расчеты:

 

 

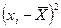
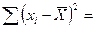
2) на основании сравнения средних значений показателей Х и Y выдвинуть рабочую гипотезу:

 

3) подтвердить выдвинутое предположение, рассчитав значение t-критерия Стьюдента и число степеней свободы по формулам:

 

 

 

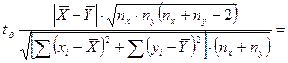
Вывод:

 

Задача 6. Определить значимость различий показателей количества подтягиваний на перекладине (можно использовать другие тесты) в группе спортсменов до начала и в конце периода тренировок силового характера, если данные таковы:

 

В начале периода х_i, кол-во раз _____________________________________

В конце периода y_i, кол-во раз _____________________________________

Решение:

 

1) занесем результаты тестирования в рабочую таблицу и сделаем соответствующие расчеты:

	хi

 

2) рассчитаем значения t-критерия Стьюдента и числа степеней свободы по формулам:

 

 

 

Вывод:

 

 

Задача 7. По результатам тестирования группы по ОФП определить визуально с помощью корреляционного поля, существует ли взаимосвязь между показателями индекса Кетле (Х) и становой силой (Y) у студентов (вид спорта)___________(n=7), если данные таковы:

 

х_i, г/см - ________________________________________________________

 

y_i, кГ - __________________________________________________________

Решение:

 

1) Представим данные тестирования в виде графика в прямоугольной системе координат:

Вывод: для того, чтобы сделать какой-то вывод, рассмотрим следующий пример.

 

Пример

Определить, зависит ли результат прыжка в длину с разбега (признак Х) от величины конечной скорости разбега (признак Y). Для ответа на этот вопрос параллельно с регистрацией результата Х каждого прыжка спортсмена или группы спортсменов регистрируют и величину конечной скорости разбега Y. Пусть они таковы:

 

Таблица

 

I
	10.7	10.5	10.3	9.8	10.1	10.5	9.1	9.6

 

Представим таблицу в виде графика в прямоугольной системе координат, где на горизонтальной оси будем откладывать длину прыжка (Х), а на вертикальной – величину конечной скорости разбега в этом прыжке (Y).

 

Рис 1. График корреляционного поля.

 

Будем называть корреляционным полем зону разброса таким образом полученных точек на графике. Визуально анализируя корреляционное поле на рисунке 1, можно заметить, что оно как бы вытянуто вдоль какой-либо прямой линии. Такая картина характерна для так называемой линейной корреляционной взаимосвязи между признаками. При этом можно в общем предположить, что с увеличением конечной скорости разбега увеличивается и длина прыжка, и наоборот. Т.е. между рассматриваемыми признаками наблюдается прямая (положительная) взаимосвязь.

Наряду с этим примером из множества других возможных корреляционных полей можно выделить следующие (рис. 2-4):

Рис. 2 Рис. 3

 

 

 

Рис. 4.

 

На рисунке 2 тоже просматривается линейная взаимосвязь, но с увеличением значений одного признака, уменьшаются значения другого, и наоборот, т.е. связь обратная или отрицательная. Можно предположить, что на рисунке 4 точки корреляционного поля разбросаны около какой-то кривой линии. В таком случае говорят, что между признаками существует криволинейная корреляционная связь.

В отношении корреляционного поля, изображенного на рисунке 3, нельзя сказать, что точки располагаются вдоль какой-то прямой или кривой линии, оно имеет сферическую форму. В этом случае говорят, что признаки Х и Y не зависят друг от друга.

Кроме этого по корреляционному полю можно примерно судить о тесноте корреляционной связи, если эта связь существует. Здесь говорят: чем меньше точки разбросаны около воображаемой усредненной линии, тем теснее корреляционная связь между рассматриваемыми признаками.

Визуальный анализ корреляционных полей помогает разобраться в сущности корреляционной взаимосвязи, позволяет высказать предположение о наличии, направленности и тесноте связи. Но точно сказать, имеется связь между признаками или нет, линейная связь или криволинейная, тесная связь (достоверная) или слабая (недостоверная), с помощью этого метода нельзя. Наиболее точным методом выявления и оценки линейной взаимосвязи между признаками является метод определения различных корреляционных показателей по статистическим данным.

 

 

Задача: Определить наличие взаимосвязи между показателями индекса Кетле (Х) и становой силы (Y) у студентов группы (вид спорта)______________ с помощью расчета рангового коэффициента корреляции Спирмена.

 

Решение:

 

1) занесем результаты тестирования в рабочую таблицу и сделаем соответствующие расчеты:

 

					-	( - )2

 

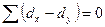
; - ранги статистических данных, т.е. места вариант в их ранжированной совокупности.

 

2) рассчитываем ранговый коэффициент корреляции по формуле:

 

Вывод:

 

 

4. Нормирование времени на задание (8 часов).

5. Форма отчета, контроля: представление письменных работ на проверку. Использование данных при написании курсовых работ.