ЗАДАНИЕ 7
ТЕМА 1: ГРАФИКИ ФУНКЦИЙ
Основные формулировки задач:
1) какие точки принадлежат промежуткам возрастания / убывания функции (указать их количество, сумму целых точек);
2) в каких точках касательная к графику функции параллельна прямой 
(или совпадает с ней);
3) найти наибольшее / наименьшее значение функции на числовом промежутке (чаще такая формулировка задания даётся не с графиком функции, а с графиком её производной!);
4) точки экстремума (их количество, сумма целых точек);
5) вычислить значение производной функции в точке;
6) найти количество точек, в которых производная функции положительна, отрицательна или равна нулю (или указать сумму таких целых точек);
7) найти количество решений уравнения 
;
8) в какой точке значение производной наибольшее / наименьшее;
9) движение материальной точки;
10) прямая, являющаяся касательной к графику функции (или параллельная касательной) – пять прототипов.
Прототип 1: На рисунке изображён график функции 
, определённой на интервале 
. Сколько из отмеченных точек 
, 
, 
, 
, 
, 
, 
, 
принадлежат промежуткам убывания функции?
Прототип 2: На рисунке изображён график функции , определённой на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой 
.
Дополнительные вопросы:
1) Сколько целых точек принадлежат промежуткам возрастания функции?
2) Сколько целых точек принадлежат промежуткам убывания функции на отрезке 
?
Прототип 3: На рисунке изображён график функции , определённой на интервале 
. Найдите наибольшее значение функции на отрезке 
.
Дополнительные вопросы:
1) Сколько целых точек принадлежат промежуткам возрастания функции на интервале 
?
2) Найдите количество точек, в которых касательная к графику функции параллельна прямой 
.
Прототип 4: На рисунке изображён график функции , определённой на интервале 
. Найдите сумму целых точек экстремума функции 
.
Дополнительные вопросы:
1) Найдите сумму целых точек, входящих в промежутки убывания функции.
2) Найдите количество точек, в которых касательная к графику функции параллельна прямой 
или совпадает с ней.
3) Найдите наименьшее значение функции на интервале 
.
Прототип 5: На рисунке изображён график функции и касательная к нему в точке с абсциссой 
. Найдите значение производной функции 
в точке 
.
Прототип 6: На рисунке изображён график функции , определённой на интервале 
. Найдите количество точек, в которых производная функции равна 0.
Дополнительные вопросы:
1) Найдите количество целых точек, входящих в промежутки возрастания функции.
2) Найдите количество точек, в которых касательная к графику функции параллельна прямой 
или совпадает с ней.
3) Найдите наименьшее значение функции на отрезке 
.
Прототип 7: На рисунке изображён график дифференцируемой функции , определённой на интервале 
. Найдите количество решений уравнения 
на отрезке 
.
Дополнительные вопросы:
1) Найдите сумму целых точек, входящих в промежутки убывания функции.
2) Найдите количество точек, в которых касательная к графику функции параллельна прямой 
.
3) Найдите наибольшее значение функции на отрезке 
.
4) Найдите количество целых точек, в которых производная функции отрицательна.
5) Найдите количество целых точек, в которых производная функции положительна.
Прототип 8: На рисунке изображён график функции . На оси абсцисс отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Дополнительный вопрос:
В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Прототип 9: Материальная точка движется прямолинейно по закону  , где  - расстояние от точки отсчёта в метрах,  - время в секундах, измеренное с начала движения. В какой момент времени (в секундах) её скорость была равна 96 м/с?
|
Дополнительный вопрос:
Найдите её скорость в м/с в момент времени 
с.
Прототип 10: Прямая  параллельна касательной к графику функции  . Найдите абсциссу точки касания.
|
Прототип 11: Прямая  является касательной к графику функции  . Найдите ординату точки касания.
|
Прототип 12: Прямая  является касательной к графику функции  .
Найдите  .
|
Прототип 13: Прямая  является касательной к графику функции  . Найдите  , учитывая, что абсцисса точки касания меньше 0.
|
Прототип 14: Прямая  является касательной к графику функции  .
Найдите  .
|
Прототип 15: Материальная точка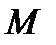 
начинает движение из точки 
и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки 
до точки 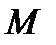со временем. На оси абсцисс откладывается время 
в секундах, на оси ординат – расстояние 
в метрах. Определите, сколько раз за время движения скорость точки 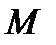обращалась в ноль (начало и конец движения не учитывайте).