РАЗДЕЛ Необратимые и термодинамически обратимые процессы

 

В общем виде процесс представляет собой изменение состояния системы под действием некоторых факторов, играющих роль движущих сил. Например, подвод тепла к веществу, находящемуся в некоторой емкости, которая отделяет его от окружающей среды, вызывает повышение температуры, что определяет его как процесс нагревания. Другим примером процесса подобного типа является расширение газа в цилиндре с подвижным поршнем при нагревании газообразного вещества. Такого рода процессы можно назвать естественными. В термодинамике их называют особым термином – термодинамически необратимые процессы, в сокращенном варианте – необратимые процессы. Название связано с тем, что естественные процессы нельзя провести в обратном направлении через те же самые состояния, которые имели место в прямом процессе. В этом смысле их нельзя обратить. Причина заключается в том, что хотя естественный процесс проявляется через изменения системы они неповторимы, индивидуальны, на каждом этапе его осуществления как в прямом, так и в обратном направлениях. В первом процессе температура тела, во втором давление газа в каждой элементарно малой части системы по ходу процесса имеют свои индивидуальные значения. В этом легко убедится, измеряя температуру, например при нагревании воды в колбе с помощью электрического нагревателя. Поэтому выражения, что в первом процессе температура повышается, во втором – давление понижается, являются всего лишь качественной характеристикой процесса.

Естественные процессы без дополнительных условий, налагаемых на их осуществление, нельзя достоверно описать физико-химическими методами с помощью функций или выражений, зависящих от конкретных параметров, поскольку в естественном процессе они не имеют физического смысла для системы в целом.

Для теоретического описания процессов их надо проводить таким образом, чтобы система в течение процесса находилась в состоянии внутреннего равновесия с характерными для данного процесса параметрами. Такое возможно если система в свою очередь находится в определенном равновесии с окружающей средой.

Предположим, что в закрытом цилиндре с невесомым поршнем, который двигается без трения, в объеме V₁ находится один моль идеального газа (рис. 1).

 

 

а б

Рис.1 Схема устройства, в котором идеальный газ совершает процесс расширения: а) начальное состояние; б) конечное состояние

Из объема над поршнем удален воздух, но поршень удерживается в состоянии равновесия грузом весом G = mg ньютонов, где m – масса груза. Все устройство находится в термостате, поддерживающем постоянную температуру Т₀. Состояние идеального газа как индивидуального вещества задается двумя параметрами, в данном случае объемом и давлением газа. Пусть в исходном состоянии они равны V₁, Р₁. Вес груза, отнесенный к единице поверхности поршня, это давление (атм)^* груза на газ.

Проведем процесс расширения газа, подводя к воде в термостате и идеальному газу теплоту от внешнего теплоисточника. Передачу тепла будем проводить чрезвычайно медленно, с тем, чтобы температура оставалась __________________________

В несистемных единицах 1 атм – давление, которое под действием силы тяжести оказывает тело массой 1033 г на см²

постоянной, а давление газа в процессе расширения имело смысл параметра состояния. Такое возможно, если разность между температурами термостата и идеального газа на каждом этапе расширения остается очень малой величиной. При расширении системой совершается объемная работа против сил внешней среды, которая состоит в преодолении силы тяжести груза.

Поскольку внутренняя энергия идеального газа зависит только от температуры, ее изменение в изотермическом процессе равно нулю, ∆U = 0. В этом случае первый закон термодинамики имеет вид: Q = W.

Теплота, подводимая к идеальному газу, в изотермическом процессе полностью расходуется на совершение работы.

Задача.

В отличие от этого в изотермическом процессе с участием реального газа, кроме совершения работы, происходит изменение внутренней энергии. Используя первый закон термодинамики обоснуйте, в каком из изотермических процессов будет совершена больше работа: с участием реального или идеального газа при поступлении в систему одного и того же количества теплоты.

Через какой-то период времени в результате поступления теплоты система перейдет из начального состояния 1 в состояние 2 с параметрами V₂, Т. При этом давление понижается с Р₁ до Р₂. При расширении газ за счет теплоты, поступающей от теплоисточника, совершает работу , количество которой в координатах Р₁, V равно заштрихованной площади на рис.2а.

 

 

 

 

 

а б

 

в г

Рис.2 Расширение газа при различных способах его проведения при Т₀ = const:

а – термодинамически обратимый процесс; б – квазистатический процесс; в, г – термодинамически необратимый процесс

 

Назовем процесс по изотерме идеальным и зададимся вопросом, а как собственно совершается этот процесс, работа которого равна заштрихованной площади? Если в один прием снять часть груза произойдет быстрое необратимое расширение газа, при этом объем и давление изменяются неопределенным образом. Когда давление газа приблизится к значению , поршень после некоторых колебаний остановится в положении , V = .

Работа против постоянного внешнего давления обладает особенностью, присущей функциям состояния: ее количество не зависит от пути процесса и определяется значениями давления и объема в начале и конце пути. Поэтому при необратимом расширении газа из состояния Р₁V₁ в состояние будет совершена работа, количество которой равно заштрихованной площади А, рис. 2г.

(1)

Работа , которую вычисляют по уравнению (1) состоит из работы изохорного процесса по пути l и изобарного процесса по пути m. Поскольку работа изохорного процесса равна нулю, работа в целом определяется работой системы против внешнего давления . Суммарный путь, на котором вычисляется работа отличается от пути е в естественном процессе. Но независимо от того как в действительности совершается естественный процесс, можно утверждать, что система (идеальный газ) совершает работу с одновременной потерей ее работоспособности, выражаемой через площадь С (по сравнению с идеальным процессом изотермического расширения). Потеря работы означает, что в необратимом процессе к идеальному газу поступает меньше теплоты от окружающей среды.

В состоянии, когда газ имеет объем параметры снова в один прием уменьшим вес груза до , равному конечному давлению газа Р₂, что приведет к необратимому расширению газа до конечного объема V₂. При этом на пути n и o будет произведена работа

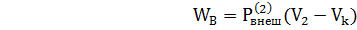(2)

с потерей работоспособности системы, которая численно выражается через площадь D.

Проведем процесс в обратном направлении, увеличивая вес груза на поршне также в два приема, сначала до , а затем до Р₁. В необратимом процессе, условно по пути g, а затем по условному пути h будет совершаться работа и (рис. 3).

(3)

(4)

 

 

 

 

а б

Рис. 3 Сжатие идеального газа под действием внешнего давления

 

В обратном процессе работа совершается силами внешней среды 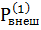и Р₁, направленными на сжатие газа с одновременным отводом теплоты в термостат. Как следует из (3), (4) и данных, представленных на рис. 3 среда совершает больше работы, чем в идеальном процессе на величину, равную площадям K и L. Поскольку процесс остается изотермическим и ∆U = 0, во внешнюю среду поступает больше теплоты (по сравнению с идеальным процессом) на величину, которая эквивалентна площадям K и L над изотермой. Как приблизить количество работы в прямом и обратном направлении к работе в идеальном процессе. Очевидно, что для этого необходимо уменьшить разность между давлением газа и внешним давлением. В итоге ступенчатые маршруты l – m – n – o и q – r – s – t будут постепенно трансформироваться в менее ломаные кривые, которые при условии равенства давления газа и внешнего давления на протяжении всего пути сольется с изотермой. Но условие равенства давления газа и внешнего давления в данном случае условие механического равновесия. Другими словами для получения максимальной работы в прямом направлении, которая по абсолютной величине равна работе в обратном направлении, процесс необходимо проводить через непрерывную совокупность равновесия между системой и окружающей средой. На каждом этапе движущая сила процесса, в данном случае давление газа, уравновешено силой сопротивления внешней среды, Р_внеш, на преодоление которой направлена работа системы.

Процесс, в котором каждое состояние представляет собой состояние равновесия между системой и средой и который можно провести в обратном направлении через состояния прямого направления, называется термодинамически обратимым процессом, сокращенно обратимым.

Увеличение движущей силы системы по отношению к силам сопротивления на малую величину позволяет направить процесс в прямом направлении, и наоборот, при чрезвычайно малом превышении сил внешней среды по отношению к движущим силам системы процесс на каждом этапе можно направить в противоположную сторону. В этом смысле процесс термодинамически обратим. Если циклический процесс провести термодинамически обратимо, в исходное состояние возвращается не только система, но и окружающая среда, при взаимодействии с которой совершался процесс. Изменения, которым подвергается система и среда в прямом направлении полностью компенсируются изменениями системы и среды, когда процесс проводится в обратном направлении. Это пока общее и абстрактное условие не выполняется для всех естественных процессов. По этой причине они термодинамически необратимы. В циклическом необратимом процессе в исходное состояние возвращается только система. В отличие от этого окружающая среда при завершении процесса находится в состоянии, которое отличается от состояния в начале процесса.

В строгом смысле, обратимый процесс сугубо теоретическое понятие, идеальная модель реального процесса. Несмотря на необычность термодинамически обратимых процессов они имеют огромное практическое значение, поскольку на основе их физико-термоинамических свойств и характеристик можно определить самые общие закономерности реальных процессов, которые очень трудно или невозможно установить, изучая реальные процессы.

Классическим примером в этом смысле являлась проблема, каким образом можно повысить коэффициент полезного действия тепловых машин. По этому поводу выдвигались разные идеи, предлагалось например, использовать вместо водяного пара атмосферный воздух. Сади Карно, французский физик (1976 – 1832), анализируя предложенный им термодинамически обратимый цикл (цикл Карно) на основе которого в принципе может работать тепловая машина, установил, что КПД тепловых машин зависит только от разности температур источника тепла Т₁ и холодильного устройства Т₂ (в качестве которого может выступать прилегающая к цилиндру воздушная атмосфера) и не зависит от природы рабочего газа

Из уравнения видно, что КПД тепловых машин увеличивается с увеличением температуры источника тепла Т₁ и понижением температуры холодильного устройства Т₂ (при Т₁→0, →1). Открытие, сделанное Карно, определило магистральное направление в развитии теплоэнергетики.

Поскольку в термодинамически обратимом процессе каждое состояние есть состояние равновесия между движущей силой процесса и противодействующей силой среды его также называют равновесным процессом. Следует заметить, что таким же термином обозначают состояние, которое наступает в необратимом процессе, когда его действующие силы становятся равными нулю. Такое состояние называют состоянием термодинамического равновесия. В термодинамически обратимом процессе они существуют, но уравновешены. В этом случае состояние равновесия есть состояние заторможенного равновесия. С учетом этих замечаний в дальнейшем термодинамически обратимый и равновесный процесс будем рассматривать как равнозначные. Обратимый процесс, в отличие от естественного, можно описать точными физико-математическими уравнениями. Примером этого является выражение работы термодинамически обратимого изотермического расширения идеального газа. Теоретические концепции, присущие обратимым процессам, составляют основу химической термодинамики и дают возможность проведения термодинамического анализа разнообразных физико-химических процессов, включая химические реакции.

Несмотря на необычные свойства обратимые процессы с определенной степенью отклонения от теоретической модели можно осуществить экспериментально и определить для них физико-термодинамические характеристики, необходимые для выявления фундаментальных свойств необратимых процессов.

Как следует из сущности обратимого процесса его практическая реализация возможна лишь при определенной неуравновешенности движущих и противодействующих сил, различие между которыми и определяет степень отклонения свойств экспериментально выполняемого процесса от его теоретической модели. Экспериментально реализуемый обратимый процесс – это процесс, в котором каждое состояние представляет собой состояние квазиравновесия^* или квазиуравновешенности между силами системы и среды.

Такой процесс можно назвать квазистатическим или квазиравновесным. Главную особенность квазистатического процесса покажем на примере изотермического расширения идеального газа. Как следует из проведенного рассмотрения, движущая сила газа, в виде давления, направлена на преодоление силы тяжести груза, которая синхронно уменьшается с понижением давления. В принципе, его можно провести таким образом, если предположить, что груз состоит из частиц очень малого размера. Если груз уменьшать, снимая частицу за частицей, расширение газа приобретет свойства квазистатического процесса. Его путь представляет собой непрерывную совокупность точек, которая фигурально _____________________________

*квази (лат) – почти, близко

показывает, что свойства квазистатического процесса незначительно отличаются от свойств идеального (рис. 2б). В частности, на рис. 2б видно, что работа квазистатического процесса – главная его характеристика, практически равна работе обратимого процесса.

Работа равновесного процесса, которую совершает система, не только превышает работу любого необратимого процесса, она максимальна по своему значению. Получить работу выше работы равновесного процесса в принципе нельзя. Это положение не зависит от типа процесса и вида работы. Доказательство этой важной закономерности базируется на соотношении, объединяющем первый и второй законы термодинамики.