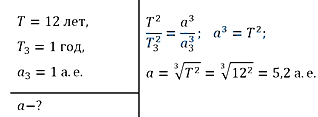Практическая работа.
Тема: Законы Кеплера. Определение масс небесных тел
Цель занятия: Освоить методику решения задач, используя законы движения планет.
Теоретические сведения (не списывать)
При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.
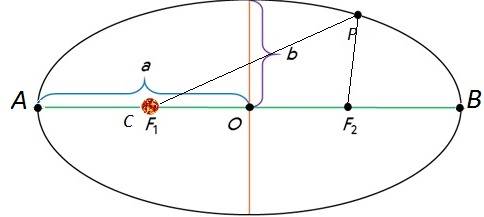
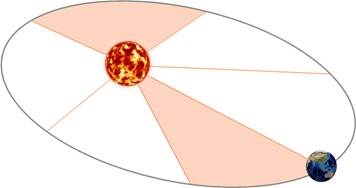
Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.
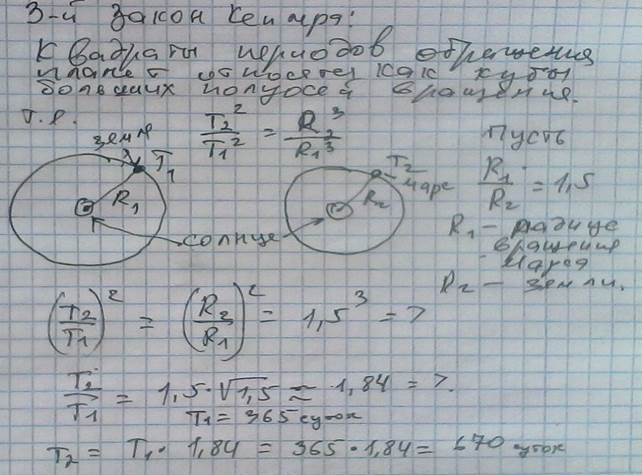
Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:
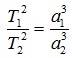
Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:
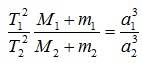
где М1 и М2 -массы каких-либо небесных тел, а m1 и m2 - соответственно массы их спутников.
Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой, а индекс 2 –к движению любого спутника вокруг планеты массой. Тогда масса планеты вычисляется по формуле:
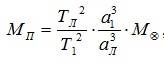
где Тл и αл- период и большая полуось орбиты спутника планеты, М⊕ -масса Земли.
Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли, выраженными в годах или сутках,
а) для внешней планеты формула имеет вид:
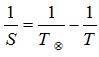
б) для внутренней планеты:
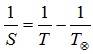
Выполнение работы
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.
Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.
Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?
(списать все задачи с решениями)
Примеры решения задач 1-4
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза дальше, чем Земля, совершает полный оборот вокруг Солнца?

Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.

Задача 5.
Задача 6.

Задача 7.Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.
(Определить период обращения астероида Россия, если большая полуось его орбиты а=2,55 а.е. Отв: 4 года)
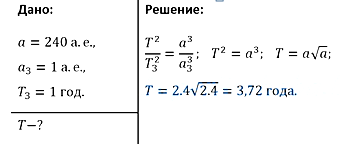
Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?