ТЕМА ПРИНЦИПЫСТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ.
Вопросы:1. Классификация оценок
Интервальные оценки. Доверительный интервал и доверительная вероятность.
Распределение хи-квадрат
Распределение Стьюдента
Распределение Фишера
Классификация оценок
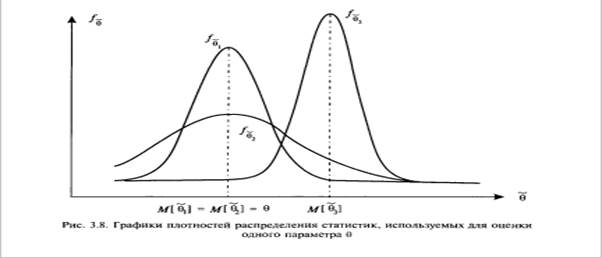
Квантиль - значение, которое заданная случайная величина не превышает с фиксированной вероятностью.
Интервальные оценки. Доверительный интервал и доверительная вероятность
В ряде задач требуется не только найти для параметра 
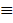
подходящее численное значение, но и оценить его точность и надежность. Требуется знать - к каким ошибкам может привести замена параметра его точечной оценкой 
и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы?
Такого рода задачи особенно актуальны при малом числе наблюдений, когда точечная оценка 
в значительной мере случайна и приближенная замена 
на может привести к серьезным ошибкам.
Чтобы дать представление о точности и надежности оценки , в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями.
Пусть для параметра получена из опыта несмещенная оценка . Мы хотим оценить возможную при этом ошибку. Назначим некоторую достаточно большую вероятность 
(например,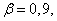 
или 
) такую, что событие с вероятностью можно считать практически достоверным, и найдем такое значение 
, для которого
(1)
Тогда диапазон практически возможных значений ошибки, возникающей при замене на θ ̃, будет 
; большие по абсолютной величине ошибки будут появляться только с малой вероятностью 
Перепишем (1) в виде:
. (2)
Равенство (2) означает, что с вероятностью неизвестное значение параметра попадает в интервал
(3)
При этом необходимо отметить одно обстоятельство. Ранее мы неоднократно рассматривали вероятность попадания случайной величины в заданный неслучайный интервал. Здесь дело обстоит иначе: величина не случайна, зато случаен интервал 
. Случайно его положение на оси абсцисс, определяемое его центром ; случайна вообще и длина интервала 
, так как величина вычисляется, как правило, по опытным данным. Поэтому в данном случае лучше будет толковать величину не как вероятность «попадания» точки в интервал , а как вероятность того, что случайный интервал накроет точку (рисунок).
Рис.
Вероятность принято называть доверительной вероятностью, а интервал - доверительным интервалом. Границы интервала : 
и 
называются доверительными границами.
Перейдем к вопросу о нахождении доверительных границ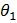 
и 
.
Пусть для параметра имеется несмещенная оценка . Если бы нам был известен закон распределения величины , задача нахождения доверительного интервала была бы весьма проста: достаточно было бы найти такое значение , для которого
.
Затруднение состоит в том, что закон распределения оценки зависит от закона распределения величины 
и, следовательно, от его неизвестных параметров (в частности, и от самого параметра ).
Чтобы обойти это затруднение, можно применить следующий грубо приближенный прием: заменить в выражении для неизвестные параметры их точечными оценками. При сравнительно большом числе опытов 
(порядка 
) этот прием обычно дает удовлетворительные по точности результаты.
В качестве примера рассмотрим задачу о доверительном интервале для математического ожидания.
Пусть произведено независимых опытов над случайной величиной , характеристики которой -математическое ожидание 
и дисперсия 
- неизвестны. Для этих параметров получены оценки:
; 
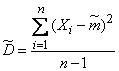. (4)
Требуется построить доверительный интервал 
, соответствующий доверительной вероятности , дляматематического ожидания величины .
При решении этой задачи воспользуемся тем, что величина 
представляет собой сумму независимых одинаково распределенных случайных величин 
, и, согласно центральной предельной теореме, при достаточно большом ее закон распределения близок к нормальному. На практике даже при относительно небольшом числе слагаемых (порядка 
) закон распределения суммы можно приближенно считать нормальным. Будем исходить из того, что величина распределена по нормальному закону. Характеристики этого закона - математическое ожидание идисперсия - равны соответственно и 
. Предположим, что величина нам известна, и найдём такую величину 
для которой
.вероятность (5)
Применяя формулу (5), выразим в левой части (5) через нормальную функцию распределения
. (6)
где 
- среднее квадратическое отклонение оценки .
Из уравнения
находим значение :
, (7)
где 
- функция, обратная 
, т. е. такое значение аргумента, при котором нормальнаяфункция распределения равна 
.
Дисперсия , через которую выражена величина 
, нам в точности не известна; в качестве ее ориентировочного значения можно воспользоваться оценкой (4) и положить приближенно:
. (8)
Таким образом, приближенно решена задача построения доверительного интервала, который равен:
, (9)
где определяется формулой (7).
Чтобы избежать при вычислении обратного интерполирования в таблицах функции , удобно составить специальную таблицу (см. табл. 1), где приводятся значения величины
в зависимости от . Величина 
определяет для нормального закона число средних квадратических отклонений, которое нужно отложить вправо и влево от центра рассеивания для того, чтобы вероятность попадания в полученный участок была равна .
Через величину доверительный интервал выражается в виде:
.