Перечень вопросов для Итогового междисциплинарного экзамена по направлению 230200 «Информационные системы» (магистерская программа «Корпоративные информационные системы»)
Исследование операций
1. Задачи линейного программирования.
2. Дискретная оптимизация в задах линейного программирования. Метод ветвей и границ.
3. Целочисленный рюкзак. Жадный алгоритм решения задачи.
4. Основные понятия теории игр. Матричные игры. Седловая точка. Принцип минимакса.
5. Смешанные стратегии. Равновесная ситуация в смешанных стратегиях.
6. Итерационный метод решения матричных игр.
7. Наглядно-графический метод решения матричных игр.
8. 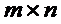 -игры. Правило доминирования. Аффинное правило. Основные этапы поиска решения матричной игры.
-игры. Правило доминирования. Аффинное правило. Основные этапы поиска решения матричной игры.
9. Сведение матричной игры к задаче линейного программирования.
10. Биматричные игры. Примеры биматричных игр (борьба за рынки, семейный спор, дилемма узников).
11. Смешанные стратегии в биматричных играх. Теорема Нэша.
12. 2×2-биматричные игры. Метод зигзага решения биматричных игр.
13. Ситуация, оптимальная по Парето. Пример множества Парето для дилеммы узника.
14. Позиционные игры. Игры с полной и неполной информацией. Нормализация позиционной игры.
Физическое и математическое моделирование
1. Методы численного дифференцирования. Привести конечно-разностные аппроксимации первой и второй производных. Рассмотреть порядок точности различных аппроксимаций производной и принципы повышения точности.
2. Численное определение корней уравнения f (x) = 0. Постановка задачи. Принципы поиска корней одним из следующих методов: деления пополам, Ньютона-Рафсона, секущих.
3. Численное интегрирование. Привести схемы численного интегрирования по формулам прямоугольников и трапеций. Рассмотреть порядок точности этих схем, обсудить принципы повышения точности.
4. Численное интегрирование дифференциальных уравнений первого порядка. Постановка задачи. Метод Эйлера.
5. Численное решение дифференциальных уравнений второго порядка в частных производных. Постановка граничных условий Дирихле и задачи на собственные значения. Конечно-разностное интегрирование краевых задач.
6. Применение метода Монте-Карло на примере численного интегрирования. Привести алгоритм решения задачи вычисления площади сложной фигуры.
7. Общие принципы получения последовательностей случайных, квазислучайных и псевдослучайных чисел. Требования, предъявляемые к генераторам псевдослучайных чисел.
8. Получение последовательности случайных (псевдослучайных) чисел, распределенных по нормальному закону, на основе равномерно распределенной последовательности (рассмотреть хотя бы один метод).
9. Сортировка числовых последовательностей. Привести примеры методов сортировки чисел с плавающей точкой, характеризующихся логарифмической вычислительной сложностью. Детально рассмотреть особенности одного из следующих методов: сортировка Шелла, сортировка всплытием Флойда, рекурсивная сортировка.
10. Метод молекулярной динамики. Уравнения движения частиц, силы и потенциалы парного взаимодействия. Алгоритм интегрирования уравнений движения по времени.
11. Расчет коэффициента диффузии частиц при моделировании многочастичных систем (в частности, кристаллов) методом молекулярной динамики.
Системы и технологии управления параллельными вычислениями
1. Общие принципы распараллеливания вычислений по данным, по инструкциям и по задачам. Особенности параллельных вычислительных систем с точки зрения реализации этих принципов.
2. Типы архитектур высокопроизводительных параллельных вычислительных систем. Преимущества и недостатки каждой архитектуры.
3. Графические процессоры архитектуры CUDA как параллельные вычислительные системы общего назначения: особенности исполнения программы в параллельных потоках, иерархия памяти, конвейерные вычисления.
4. Особенности программирования графических процессоров архитектуры CUDA на примере задачи скалярного перемножения матриц.
5. Особенности программирования графических процессоров архитектуры CUDA на примере распараллеливания алгоритма молекулярной динамики (в частности, процедуры расчета парных и результирующих сил).
6. Программирование графических процессоров архитектуры CUDA на примере вычисления потока нейтронов через пластину методом Монте-Карло.