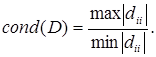Пусть X – матрица данных порядка N x p, где N>p, и пусть r – ранг матрицы X. Чаще всего r=p, но приводимый ниже результат охватывает общий случай, он справедлив и при условии r<p.
Теорема о сингулярном разложении утверждает, что
 (10)
(10)
где V – матрица порядка N x r, столбцы которой ортонормированы, т.е.  ; U – матрица с ортонормированными столбцами порядка p x r; таким образом,
; U – матрица с ортонормированными столбцами порядка p x r; таким образом,  ; Г – диагональная матрица порядка r x r, диагональные элементы которой
; Г – диагональная матрица порядка r x r, диагональные элементы которой 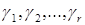 , называемые сингулярными числами матрицы X, положительны. Используя диагональные элементы
, называемые сингулярными числами матрицы X, положительны. Используя диагональные элементы  матрицы Г, столбцы
матрицы Г, столбцы  матрицы V, и столбцы
матрицы V, и столбцы 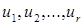 матрицы U, сингулярное разложение матрицы X, определяемое по (10), можно записать в виде:
матрицы U, сингулярное разложение матрицы X, определяемое по (10), можно записать в виде:
 (11)
(11)
Имеют место следующие фундаментальные соотношения.
· Квадратная симметричная матрица XX' порядка N x N, имеет r положительных и N–r нулевых собственных чисел. Положительными собственными числами XX' являются 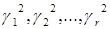 , а соответствующими собственными значениями –
, а соответствующими собственными значениями –  . Таким образом, сингулярные значения
. Таким образом, сингулярные значения  – это положительные квадратные корни из положительных собственных чисел матрицы XX', а столбцы матрицы V – соответствующие собственные векторы.
– это положительные квадратные корни из положительных собственных чисел матрицы XX', а столбцы матрицы V – соответствующие собственные векторы.
· Квадратная симметричная матрица X'X порядка p x p, имеет r положительных и p–r нулевых собственных чисел. Положительными собственными числами X'X являются  , а соответствующими собственными значениями –
, а соответствующими собственными значениями –  , таким образом, сингулярные значения
, таким образом, сингулярные значения  – это положительные квадратные корни из положительных собственных чисел матрицы X'X, а столбцы матрицы U – соответствующие собственные векторы.
– это положительные квадратные корни из положительных собственных чисел матрицы X'X, а столбцы матрицы U – соответствующие собственные векторы.
Положительные собственные числа матрицы X'X и XX' совпадают и равны  . Более того, если um – собственный вектор матрицы X'X, а vm – собственный вектор матрицы XX', соответствующие одному и тому же собственному числу
. Более того, если um – собственный вектор матрицы X'X, а vm – собственный вектор матрицы XX', соответствующие одному и тому же собственному числу  , то um и vm связаны следующим соотношением
, то um и vm связаны следующим соотношением
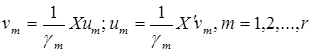 (12)
(12)
Эти соотношения дают возможность вычислять  , зная
, зная 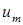 , и наоборот. В компактной форме эти соотношения можно записать следующим образом:
, и наоборот. В компактной форме эти соотношения можно записать следующим образом:
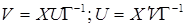 . (13)
. (13)
Исследование матрицы X'X в факторном анализе называется R- модификацией, а XX' – Q– модификацией. Соотношения (12)–(13) показывают, что результаты Q– модификации можно получить по результатам R– модификации и наоборот.
Практическая последовательность нахождения сингулярного разложения следующая.
1. Вычисляется X'X или XX', в зависимости от того, порядок какой матрицы меньше. Предположим, что в данном случае это X'X.
2. Вычисляются положительные собственные числа  матрицы X'X и соответствующие им собственные векторы
матрицы X'X и соответствующие им собственные векторы 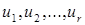 .
.
3. Находятся сингулярные числа  .
.
4. Вычисляются  по соотношению (11).
по соотношению (11).
Пусть в разложении (11) собственные числа расположены в порядке убывания. Аппроксимационные свойства соотношения (11) являются еще более фундаментальными, чем само соотношение. Эти свойства вытекают из решения следующих двух задач.
Задача 1. Дана симметричная матрица S, порядка p x p и ранга r с неотрицательными собственными значениями. Требуется найти симметричную матрицу Т, размерности p x p, с неотрицательными собственным значениями заданного ранга k, k<r, являющуюся наилучшей аппроксимацией матрицы S в смысле наименьших квадратов.
Задача 2. Дана прямоугольная матрица X, порядка N x p и ранга r и число k<r. требуется найти матрицу W порядка p x p и ранга k, наилучшим образом аппроксимирующую матрицу X в смысле наименьших квадратов.
Решением этих двух задач являются матрицы:
 (14)
(14)
представляющие собой суммы k первых членов в соответствующем разложении. Матрицы T и W называются наилучшими в смысле наименьших квадратов “матричными аппроксимациями меньшего ранга” для матриц S и X соответственно. Свойство наилучшей аппроксимации в смысле наименьших квадратов можно выразить следующим образом: матрица T ближе всего к матрице S в том смысле, что сумма квадратов всех элементов матрицы S–T минимальна. Аналогично матрица W ближе всего к матрице X в том смысле, что минимальна сумма квадратов элементов матрицы X–W. Мерой близости или качества аппроксимации считается относительная величина 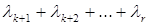 , т.е. сумма r–k наименьших собственных чисел матрицы X’X. Иногда мерой качества аппроксимации считается относительная величина
, т.е. сумма r–k наименьших собственных чисел матрицы X’X. Иногда мерой качества аппроксимации считается относительная величина
 (15)
(15)
или функция от нее.
Рассмотрим наиболее распространенный случай p=r.
Матрица S может быть ковариационной матрицей p линейно независимых переменных. Матрица T также может представлять собой ковариационную матрицу p переменных, но так как ранг матрицы T k<p, то эти p переменных линейно зависят от k переменных. Таким образом, p исходных переменных, ковариационная матрица которых есть S, могут быть приближенно выражены через k переменных.
Во второй задаче исходную матрицу X порядка N x p можно выразить как X=VГU’, где V – матрица порядка N x p c ортонормированными столбцами; Г – диагональная матрица порядка p x p, а U – квадратная ортогональная матрица порядка p x p.
Матричную аппроксимацию меньшего ранга W можно представить в виде

где  – состоит из первых k столбцов матрицы V,
– состоит из первых k столбцов матрицы V, 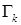 – из первых k строк или столбцов матрицы Г, а
– из первых k строк или столбцов матрицы Г, а  – из первых k столбцов матрицы U. поскольку W»X, то
– из первых k столбцов матрицы U. поскольку W»X, то
 (16)
(16)
При умножении этой матрицы справа на 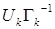 получаем
получаем
 (17)
(17)
Матрица 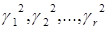 порядка pxk определяет преобразование строк матрицы X из евклидова p –мерного пространства в евклидово k –мерное пространство; уравнение (16) показывает, что существует преобразование матрицы X порядка N x p в матрицу порядка N x k. Матрица X содержит N точек в p –мерном евклидовом пространстве, которые приближенно могут быть спроектированы в k –мерное евклидово пространство. матрица
порядка pxk определяет преобразование строк матрицы X из евклидова p –мерного пространства в евклидово k –мерное пространство; уравнение (16) показывает, что существует преобразование матрицы X порядка N x p в матрицу порядка N x k. Матрица X содержит N точек в p –мерном евклидовом пространстве, которые приближенно могут быть спроектированы в k –мерное евклидово пространство. матрица  определяет координаты этих точек в k –мерном евклидовом пространстве.
определяет координаты этих точек в k –мерном евклидовом пространстве.
QR–разложение
Теорема 2. Пусть А – m ´ n– матрица. Существует ортогональная m ´ m– матрица Q такая, что в матрице QA=R под главной диагональю стоят только нулевые элементы.
Доказательство. Выберем ортогональную m ´ m– матрицу Q в соответствии с преобразованием Хаусхолдера (9), так, чтобы первый столбец Q 1 A имел нулевые компоненты со 2–ой по m –ю. Далее выбираем ортогональную (m- 1 ) ´ (m– 1 )– матрицу P 2 следующим образом. Будучи применена к m– 1 вектору, составленному из компонент со 2–ой по m –ю второго столбца матрицы Q 1 A, она аннулирует компоненты с 3–ей по m –ю этого вектора. Матрица преобразования

ортогональна, и Q 2 Q 1 A имеет в первых двух столбцах нули под главной диагональю. Продолжая таким образом, можно построить произведение, состоящее максимум из n ортогональных преобразований, которое трансформирует А к верхней треугольной форме. Формальное доказательство можно получить методом конечной индукции.
Полученное представление матрицы произведением ортогональной и верхней треугольной матриц называется QR –разложением.
Теорема 3. Пусть А – m´n– матрица ранга к, причем k<n£m. Существуют ортогональная m´m– матрица Q и m´n– матрица перестановки P такие, что
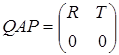 , (18)
, (18)
где R – верхняя треугольная к´к– матрица ранга к.
Доказательство. Выберем матрицу перестановки Р таким образом, чтобы первые к столбцов матрицы AP, были линейно независимы. Согласно теореме 2, найдется ортогональная m´m– матрица Q такая, что QAP будет верхней треугольной. Поскольку первые к столбцов АР линейно независимы, это будет верно для первых к столбцов QAP.
Все элементы матрицы QAP, стоящие на пересечении строк с номерами к+1,...,m и столбцов с номерами к+1,...,n, будут нулями. В противном случае rankQAP>k, что противоречит предположению rankA=k. Итак, QAP имеет форму, указанную правой частью (4). Теорема доказана.
Подматрицу[ R:T ] из правой части (18) можно теперь преобразовать к компактной форме, требуемой от матрицы R из теоремы 2. Это преобразование описывает следующая лемма.
Лемма 1. Пусть [ R:T ] – к´к– матрица, причем R имеет ранг к. Существует ортогональная n´n– матрица W такая, что

где 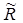 – нижняя треугольная матрица ранга к.
– нижняя треугольная матрица ранга к.
Доказательство леммы вытекает из теоремы 3, если отождествить величины n, k, [ R:T ], W из формулировки леммы с соответствующими величинами m, n, A T, Q T теоремы 3.
Используя теорему 3 и лемму 1 можно доказать следующую теорему.
Теорема 4. Пусть А – m´n– матрица ранга к. Найдутся ортогональная m´m– матрица Н и ортогональная n´n– матрица К такие, что
 (19)
(19)
причем R 11 – невырожденная треугольная к´к– матрица.
Заметим, что выбором Н и К в уравнении (19) можно добиться, чтобы R 11 была верхней или нижней треугольной.
В (19) матрица А представлена произведением A=HRK T, где R – некоторая прямоугольная матрица, ненулевые компоненты которой сосредоточены в невырожденной треугольной подматрице. Далее мы покажем, что эту невырожденную подматрицу R можно упростить далее до невырожденной диагональной матрицы. Это разложение тесно связано со спектральным разложением симметричных неотрицательно определенных матриц A T A и AA T (см. 11).
Теорема 5. Пусть А – m´n– матрица ранга k. Тогда существуют ортогональная m´m– матрица U, ортогональная n´n– матрица V и диагональная m´n– матрица S такие, что
U T AV=S, A=USV T (20)
Матрицу S можно выбрать так, чтобы ее диагональные элементы составляли невозрастающую последовательность; все эти элементы неотрицательны и ровно к из них строго положительны.
Диагональные элементы S называются сингулярными числами А. Докажем сперва лемму для специального случая m=n=rankA.
Лемма 2. Пусть А – n´n –матрица ранга n. Тогда существует ортогональная n´n –матрица U, ортогональная n´n –матрица V и диагональная n´n –матрица S такие, что U T AV=S, A=USV T и последовательные диагональные элементы S положительны и не возрастают.
Доказательство леммы. Положительно определенная симметричная матрица A T A допускает спектральное разложение
A T A = VDV T, (21)
где V – ортогональная n´n –матрица, а D – диагональная матрица, причем диагональные элементы D положительны и не возрастают. Определим S как диагональную n´n –матрицу, диагональные элементы которой суть положительные квадратные корни из соответствующих диагональных элементов D. Таким образом
D=S T S=S 2, S -1 D S-1= I. (22)
Определим матрицу
U=AVS -1 (23)
Из (21), (22), (23) и ортогональности V следует, что
U T U=S -1 V T A T AVS -1= S -1 DS -1=I т.е. U ортогональна. Из (23) и ортогональности V выводим USV T= AVS -1 SV T= AVV T= A Лемма доказана.
Доказательство теоремы 5. Пусть A=HRK T, где H, R, K T имеют свойства, указанные в теореме 4. Так как R11 из (19) – невырожденная треугольная к´к– матрица, то согласно лемме 2, можно написать
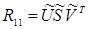 (24)
(24)
Здесь  и
и 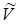 – ортогональные к´к– матрицы, а
– ортогональные к´к– матрицы, а  – невырожденная диагональная матрица, диагональные элементы которой положительны и не возрастают. Из (24) следует, что матрицу R в уравнении (19) можно записать в виде
– невырожденная диагональная матрица, диагональные элементы которой положительны и не возрастают. Из (24) следует, что матрицу R в уравнении (19) можно записать в виде
 (25)
(25)
где:
 – ортогональная m´m– матрица;
– ортогональная m´m– матрица;
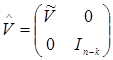 – ортогональная n´n– матрица;
– ортогональная n´n– матрица;
 – ортогональная m´n– матрица;
– ортогональная m´n– матрица;
Теперь, определяя U и V формулами
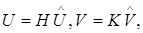 (26)
(26)
заключаем из (24) – (26), что A=USV T, где U, S, V имеют свойства, указанные в формулировке теоремы 5. Это завершает доказательство.
Заметим, что сингулярные числа матрицы А определены однозначно, в то время, как в выборе ортогональных матриц U, V есть произвол. Пусть s – сингулярное число А, имеющее кратность l. Это значит, что для упорядоченных сингулярных чисел найдется индекс I такой, что

Положим k=min(m,n), и пусть Q – ортогональная к´к– матрица вида

Здесь Р – ортогональная l´l– матрица Если A=USV T – сингулярное разложение А и s i=…= s i+ l -1, то сингулярным разложением А будет также и  , где
, где  .
.
Число обусловленности
Некоторые вычислительные задачи поразительно чувствительны к изменению данных. Этот аспект численного анализа не зависит от плавающей арифметики или выбранного алгоритма.
Например:
Найти корни полинома: (x -2)2=10-6
Корни этого уравнения есть 2+10-3 и 2-10-3. Однако изменение свободного члена на 10-6 может вызвать изменение в корнях, равное 10-3.
Операции с матрицами, как правило, приводят к решению систем линейных уравнений. Коэффициенты матрицы в правой части системы линейных уравнений редко известны точно. Некоторые системы возникают из эксперимента, и тогда коэффициенты подвержены ошибкам наблюдения. Коэффициенты других систем записываются формулами, что влечет за собой ошибки округлений. В связи с этим необходимо знать, как влияют ошибки в коэффициентах матрицы на решение. Именно для этого вводится понятие обусловленности матрицы.
По определению число обусловленности есть величина 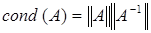 . Для более подробного описания числа обусловленности нам понадобится понятие нормы в пространстве векторов и матриц.
. Для более подробного описания числа обусловленности нам понадобится понятие нормы в пространстве векторов и матриц.
Нормой вектора x в пространстве векторов  называется функционал, обозначаемый
называется функционал, обозначаемый  , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) положительной определенности – 
2) положительной однородности –  ;
;
3) неравенству треугольника – 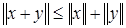 .
.
Нормой квадратной матрицы А в пространстве матриц, согласованной с нормой вектора  называется функционал
называется функционал 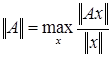 , удовлетворяющий условиям 1 – 3 для нормы вектора:
, удовлетворяющий условиям 1 – 3 для нормы вектора:
1) 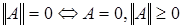 ;
;
2) 
3) 
4) мультипликативное неравенство – 
Наиболее употребимы следующие нормы для векторов:
· норма суммы модулей 
· евклидова норма 
· норма максимума модуля 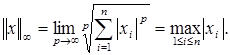
Нормы матриц:
· 
· 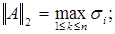
· 
Здесь  являются сингулярными числами[3] матрицы А; это положительные значения квадратных корней
являются сингулярными числами[3] матрицы А; это положительные значения квадратных корней 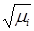 из собственных значений
из собственных значений  матрицы АТА (которая при невырожденной матрице А положительно определена[4], в противном случае положительно полуопределена (неотрицательно определена[5]) и поэтому имеет только вещественные собственные значения ³ 0). Для вещественных симметричных матриц сингулярные числа равны абсолютным величинам собственных значений:
матрицы АТА (которая при невырожденной матрице А положительно определена[4], в противном случае положительно полуопределена (неотрицательно определена[5]) и поэтому имеет только вещественные собственные значения ³ 0). Для вещественных симметричных матриц сингулярные числа равны абсолютным величинам собственных значений:  .
.
Умножение вектора х на матрицу А приводит к новому вектору Ах, норма которого может очень сильно отличаться от нормы вектора х.
Область изменений может быть задана двумя числами

Максимум и минимум берутся по всем ненулевым векторам. Заметим, что если А вырождена, то m= 0. Отношение M/m называется числом обусловленности матрицы А,
 (7)
(7)
Рассмотрим норму обратной[6] матрицы  .
.
Для матрицы А существует сингулярное разложение  , тогда
, тогда 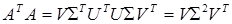 , отсюда
, отсюда  . Аналогично для обратной матрицы
. Аналогично для обратной матрицы  и
и  . Отсюда следует, что собственные числа матрицы
. Отсюда следует, что собственные числа матрицы  – 1 / есть величины, обратные собственным числам матрицы
– 1 / есть величины, обратные собственным числам матрицы  –. При этом очевидно, что
–. При этом очевидно, что  . Из последнего выражения вместе с (7) следует
. Из последнего выражения вместе с (7) следует  . Таким образом обусловленность матрицы равна произведению нормы матрицы на норму обратной матрицы.
. Таким образом обусловленность матрицы равна произведению нормы матрицы на норму обратной матрицы.
Рассмотрим систему уравнений Ax=b, и другую систему, полученную изменением правой части: A(x+Dx)=b+Db. Будем считать Db ошибкой в b, а Dx соответствующей ошибкой в x, хотя нам нет необходимости считать ошибки малыми. Поскольку A(Dx)=Db, то определения M и m немедленно приводят к неравенствам  Следовательно, при m¹ 0,
Следовательно, при m¹ 0,
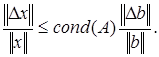
Величина 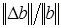 есть относительное изменение правой части, а величина
есть относительное изменение правой части, а величина 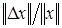 – относительная ошибка, вызванная этим изменением. Аналогичные выкладки можно провести не только с элементами вектора правой части но и с элементами самой матрицы А и найти зависимость между относительным изменением элементов матрицы и относительной ошибкой вызванной этим изменением. Отсюда следует, что число обусловленности выполняет роль множителя в увеличении относительной ошибки.
– относительная ошибка, вызванная этим изменением. Аналогичные выкладки можно провести не только с элементами вектора правой части но и с элементами самой матрицы А и найти зависимость между относительным изменением элементов матрицы и относительной ошибкой вызванной этим изменением. Отсюда следует, что число обусловленности выполняет роль множителя в увеличении относительной ошибки.
Приведем некоторые свойства числа обусловленности. Ясно, что M³m и поэтому cond(А)³ 1. Если Р – матрица перестановок[7], то компоненты вектора Px лишь порядком отличаются от компонент вектора х. Отсюда следует, что  и cond(P)= 1. В частности cond(I)= 1. Если А умножается на скаляр с, то cond(cА)= cond(А). Если D – диагональная матрица, то
и cond(P)= 1. В частности cond(I)= 1. Если А умножается на скаляр с, то cond(cА)= cond(А). Если D – диагональная матрица, то