Алгоритмы
QR –алгоритм начинается с разложения матрицы по Грамму-Шмидту 
, затем меняются местами сомножители: 
Эта матрица подобна первоначальной, 
Этот процесс продолжается, причем собственные значения не изменяются:
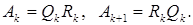
Эта формула описывает QR –алгоритм без сдвигов. Обычно время которое тратится на такой процесс пропорционально кубу размерности матрицы – n 3. Необходимо процесс ускорить, для чего используется предварительное приведение матрицы А к форме Хессенберга [8] а также используется алгоритм со сдвигом. Форма Хессенберга представляет из себя верхнюю треугольную матрицу (верхняя форма Хессенберга) у которой сохранена одна диагональ ниже главной, а элементы ниже этой диагонали равны нулю. Если матрица симметрична, то легко видеть, что матрица Хессенберга превращается в трехдиагональную матрицу [9]. При использовании матрицы Хессенберга время процесса пропорционально n 2, а при использовании трехдиагональной матрицы – n.
Можно использовать другие соотношения
где Qs – унитарная, а Ls – нижняя треугольная матрица. Такой алгоритм носит название QL –алгоритма.
В общем случае, когда все собственные значения матрицы различны, последовательность матриц As имеет пределом нижнюю треугольную матрицу 
, диагональные элементы которой представляют собой собственные значения матрицы А, расположенные в порядке возрастания их модулей. Если матрица А имеет кратные собственные значения, то предельная матрица не является треугольной, а содержит диагональные блоки порядка p, соответствующие собственному числу 
кратности p.
В общем случае, наддиагональный элемент 
матрицы As на s -ом шаге асимптотически равен 
, где kij – постоянная величина. Сходимость QL –алгоритма вообще говоря недостаточна. Сходимость можно улучшить, если на каждом шаге вместо матрицы As использовать матрицу As - ksI (QL –алгоритм со сдвигом). Последовательность вычислений в этом случае описывается следующими соотношениями:
|
|
которые определяют матрицу 
. При этом асимптотическое поведение элемента определено соотношением 
, а не 
, как прежде. Если сдвиг ks выбрать близко к величине 
(наименьшее собственное значение), то в пределе внедиагональные элементы первой строки будут очень быстро стремиться к нулю. Когда ими можно пренебречь, элемент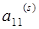 
с рабочей точностью равен 
, остальные являются собственными значениями оставшейся матрицы n- 1 - го порядка. Тогда, если QL –алгоритм выполнен без ускорения сходимости, то все равно 
, и поэтому автоматически можно выделить величину сдвига ks.
Если матрица А эрмитова, то очевидно, что и все матрицы Аs эрмитовы; если А действительная и симметричная, то все Qs ортогональны и все Аs действительны и симметричны.
Реализация разложения
Таким образом, разложение 
производится в два этапа. Сначала матрица А посредством двух конечных последовательностей преобразований Хаусхолдера где 
, приводится к верхней двухдиагональной форме следующего вида:
Далее реализуется итерационный процесс приведения двухдиагональной матрицы J 0 к диагональной форме, так что имеет место следующая последовательность: 
где 
а Si и Ti – диагональные матрицы.
Матрицы Ti выбираются так, чтобы последовательность матриц 
сходилась к двухдиагональной матрице. Матрицы же Si выбирают так, чтобы все Ji сохраняли двухдиагональную форму. Переход 
осуществляется с помощью плоских вращений (10) – преобразований Гивенса. Отсюда, 
где
|
|
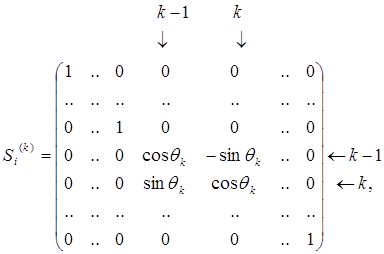
а матрица 
вычисляется аналогично с заменой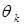 
на 
.
Пусть начальный угол 
произволен, однако следующие значения угла необходимо выбирать так, чтобы матрица Ji+ 1 имела ту же форму, что и Ji. Таким образом 
не аннулирует ни одного элемента матрицы, но добавляет элемент 
; 
аннулирует 
но добавляет 
; 
аннулирует 
но добавляет 
и т.д., наконец, 
аннулирует 
и ничего не добавляет.
Этот процесс часто называют процессом преследования. Так как 
, то 
, и Mi+ 1 – трехдиагональная матрица, точно так же, как и Mi. Начальный угол 
можно выбрать так, чтобы преобразование 
было QR –преобразованием со сдвигом, равным s.
Обычный QR –алгоритм со сдвигом можно записать в следующем виде:
где 
– верхняя треугольная матрица. Следовательно, 
. Параметр сдвига s определяется собственным значением нижнего минора (размерности 2´2) матрицы Mi. При таком выборе параметра s метод обладает глобальной и почти всегда кубичной сходимостью.