Пример расчета (задача № 20)

Плоская задача в декартовых координатах

На практике различают два вида плоской задачи - плоскую де­формацию и обобщенное плоское напряженное состояние.

В случае плоской деформации линейные деформации вдоль од­ной из координатных осей, например, оси z отсутствуют, а напря­жения имеются e _zz = 0; s _zz ¹ 0. Примером плоской деформации может служить деформация длинной стенки постоянного сечения, в случаях когда внешние нагрузки расположены в плоскостях, перпендикулярных оси z, где ось z направлена вдоль стенки.

Примером обобщенного плоского напряженного состояния мо­жет служить напряженно-деформированное состояние тонкой пла­стины, в случае, когда внешние нагрузки приложены по ее контуру и равномерно распределены по толщине пластины рис. 10.5.

Рис. 10.5

Расположим начало системы координат x, y, z в серединной плоскости пластины, а ось z направим перпендикулярно к ней, тогда будем иметь: e _zz ¹ 0; s _zz = 0.

Плоская задача теории упругости, как и объемная задача, может быть решена как в перемещениях, так и в напряжениях.

Здесь рассмотрим решение плоской задачи обобщенного на­пряженного состояния в напряжениях допуская, что объемной си­лой является собственный вес, постоянный для всех точек тела. Пусть g _y - вес единицы объема тела. В данном случае искомыми величинами являются следующие три компонента вектора напря­жений s _xx, s _yy, t _xy. Предполагая, что s _zz = 0 и все производные по оси z равны нулю, основные уравнения теории упругости значи­тельно упростятся и примут вид:

уравнения равновесия

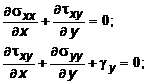(10.27)

уравнения неразрывности деформации

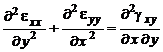; (10.28)

физические уравнения, т.е. закон Гука:

(10.29)

В результате совместного рассмотрения этих выражений полу­чим:

Ѳ (s _xx + s _yy ) = 0, (10.30)

где - оператор Лапласа.

Следовательно, решение краевой задачи теории упругости в напряжениях, в случае обобщенного плоского напряженного сос­тояния, упрощается и сводится к решению уравнения (10.30) с учетом граничных условий, заданных на контуре тела:

,

где v - внешняя нормаль к площадке; X, Y - компоненты полного напряжения на границе по осям x и y.

Решение плоской задачи теории упругости значительно упро­щаются с использованием функции напряжений Эри j (x, y), вы­бранной таким образом, чтобы уравнения равновесия (10.27) пре­вращались бы в тождества, т.е.:

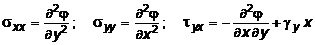. (10.31)

Подставляя первые два выражения (10.31) в (10.30) получим:

. (10.32)

Таким образом, решение плоской задачи в напряжениях сво­дится к решению уравнения (10.32) с учетом заданных в напряже­ниях граничных условий.

Пример расчета (задача № 19)

Определить главные напряжения и направления главных пло­щадок, если напряженное состояние в точке задано следующими компонентами: s _xx = 50 МПа, s _yy = -20 МПа, s _zz = 30 МПа, t _xy =
= -10 МПа, t _yz = 10 МПа, t _zx = 10 МПа.

Решение

1. В соответствии с (10.14) определяем инварианты заданного напряженного состояния:

I ₁ = s _xx + s _yy + s _zz = 50 - 20 + 30 = 60 МПа;

I ₂= s _xx s _yy + s _yy s _zz +s _xx s _zz - = 50×(-20) +
+ (-20)×30 + 30×50 - 10² - 10² - 10² = -400 МПа.

I ₃=s _xx s _yy s _zz - =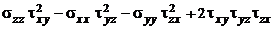
= 50×(-20)×30 -50×10² -(-20)×10² -30 -10² + 2×(-10)×10×10 =-38000 МПа.

2. Определяем коэффициенты уравнения (10.13). Если сделать

замену неизвестного S = s = x + , то из (10.13) получаем приве­денное уравнение:

,

где

p = -400- =-1600, q = .

Определим дискриминант приведенного уравнения:

.

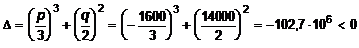Так как дискриминант отрицателен, значит все корни приве­денного уравнения вещественные.

3. Вычисление величин главных напряжений. Для решения приведенного уравнения применим формулу Кардано:

,

где

cos j ®j = 124,63°;

cos (j/3) = cos (41,54°) = 0,7484; cos (j/3+2 p/3)=-0,9486; cos (j/3 + + 4 p/3) = 0,2;

;

.

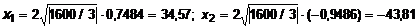Окончательно получим:

s₁ = 34,57 + 60/3 = 54,57 МПа;

s₂ = -43,81 + 60/3 = -23,8 МПа;

s₃ = 9,22 + 60/3 = 29,22 МПа.

Проверка правильности вычисления главных напряжений: так как I ₁, I ₂ и I ₃ - инварианты, значит их значения постоянны. Ранее были получены их значения в заданной системе координат. Сейчас же найдем их значения в главной системе координат:

I ₁ = s₁ + s₂ + s₃ = 54,57 - 23,8 + 29,22 = 59,99 МПа;

I ₂= s₁ s₂ + s₁ s₃ + s₂ s₃ = 54,57×(-23,8) - 23,8×29,22 + 29,22×54,57 =
= -400,2 МПа;

I ₃ = s₁ s₂ s₃ = 54,57×(-23,8)×29,22 = -37950 МПа.

Результаты вычислений I ₁, I ₂ и I ₃ в рамках допустимых откло­нений совпадают с результатами, полученными в п. 1 решения.

4. Определяем направляющие косинусы главных площадок. Си­стема уравнений для определения l ₁, m ₁, n ₁ имеет следующий вид:

(50 - 54,57) l ₁ - 10 m ₁ + 10 n ₁ = 0;

-10 l ₁ - (20 + 54,57) m ₁ + 10 n ₁ =0;

.

Решение этой системы: l ₁ = -0,9334; m ₁ = 0,0785; n ₁ = -0,3486. Условия проверки выполняются: (-0,9334)² +(-0,3486)² + 0,0785² @1.

Система уравнений для определения l ₂, m ₂, n ₂ имеет следую­щий вид:

(50 + 23,81) l ₂ -10 m ₂ + 10 n ₂ = 0;

-10 l ₂ + (-20 + 23,81) m ₂ + 10 n ₂ =0;

.

Решение этой системы: l ₂ = -0,159; m ₂ = 0,965; n ₂ = -0,2086. Условия проверки выполняются: 0,159² + 0,965² + (-0,2086)² @ 1.

Система уравнений для определения l ₃, m ₃, n ₃ имеет следую­щий вид:

(50 - 29,22) l ₃ - 10 m ₃ + 10 n ₃ = 0;

-10 l ₃ + (-20 - 29,22) m ₃ + 10 n ₃ =0;

.

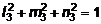Решение этой системы: l ₃ = 0,5515; m ₃ = 0,4328; n ₃ = -0,7132. Условия проверки выполняются: 0,5515² + 0,4328² + (-0,7132)² @ 1.

 

Пример расчета (задача № 20)

Рис. 10.6

Дана прямоугольная неве­сомая пластина (рис. 10.6), по кромкам которой действуют внешние силы, равномерно распределенные по ее толщи­не, равной единице. Под дей­ствием этих сил в пластине возникает обобщенное напря­женное состояние, описывае­мое функцией напряжений в виде полинома четвертой степени

j = 2 b x ³ - 3 x ² y ² + y ⁴.

Требуется:

1. Проверить возможность существования такой функции на­пряжений;

2. По функции напряжений найти выражения компонентов на­пряжений;

3. Выяснить характер распределенных по кромкам пластины внешних сил, под действием которых имеет место данная система напряжений, и построить эпюры напряжений;

4. По полученным эпюрам напряжений, принимая их за эпюры распределенной внешней нагрузки, произвести проверку равнове­сия пластины.

Решение

1. Проверить возможность существования такой функ­ции напряжений. Для выполнения проверки существования за­данной функции напряжений выполним ее дифференцирование:

;

;

.

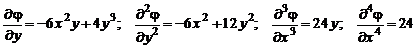Подставив четвертые производные в бигармоническое уравне­ние (10.32), видим, что оно удовлетворяется: 0 + 2 (-12) + 24 = 0. Следовательно, напряженное состояние пластины, выраженное за­аной функцией напряжений, возможно.

2. По функции напряжений найти выражения ком­понентов напряжений. Компоненты напряжений, действую­щих по кромкам пластины, равны:

3. Выяснить характер распределенных по кромкам пластины внешних сил, под действием которых имеет место данная система напряжений, и построить эпюры напряжений. Используя функциональные компоненты напряже­ний в пластине, построим соответствующие эпюры напряжений по контуру пластины на каждой ее боковой стороне.

Сторона 0-1-2 (x = 0, 0 £ y £ b). На этой грани действуют напряжения s _xx = 12 y ² ; t _xy = 0:

y = 0 (точка 0) s _xx = 0, t _xy = 0,

y = b /2 (точка 1) s _xx = 3 b ², t _xy = 0,

y = b (точка 2) s _xx = 12 b ², t _xy = 0.

Сторона 2-3 (0 £ x £ 2 b, y = b). На этой грани действуют напряжения s _yy = 12 b x - 6 b ²; t _xy = 12 b x:

x = 0 (точка 2) s _yy = -6 b ², t _xy = 0,

x = 2 b (точка 3) s _yy = 18 b ², t _xy = 24 b ².

Сторона 3-4-5 (x = 2 b, 0 £ y £ b). На этой грани действуют напряжения s _xx = -24 b ² + 12 y ²; t _xy = 24 b y:

y = 0 (точка 5) s _xx = -24 b ², t _xy = 0,

y = b /2 (точка 4) s _xx = -21 b ², t _xy = 12 b ²,

y = b (точка 3) s _xx = -12 b ², t _xy = 24 b ².

Сторона 0-5 (0 £ x £ 2 b, y = 0). На этой грани действуют напряжения s _yy = 12 b x; t _xy = 0:

x = 0 (точка 0) s _yy = 0, t _xy = 0,

x = 2 b (точка 5) s _yy = 24 b ², t _xy = 0.

По полученным результатам строим эпюры s _xx, s _yy и t _{xy ,} ко­торые приведены на рис. 10.7.

Рис. 10.7

4. По полученным эпюрам напряжений, принимая их за эпюры распределенной внешней нагрузки, произвести про­верку равновесия пластины. Выполним проверку равновесия пластины. Для этой цели найдем равнодействующие внешних сил, действующих по кромкам пластины (рис. 10.8):

Подсчет значений равнодействующих сил (рис. 10.8):

Далее определяются статические моменты площадей эпюры нормальных напряжений, действующих по кромкам пластины, от­носительно координатных осей x и y, с целью вычисления коорди­нат точек приложения равнодействующих сил от нормальных на­пряжений:

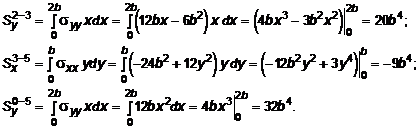
Расстояния от точек действия результирующих нормальных сил до соответствующих координатных осей принимают следующие значения (рис. 10.8):

Рис. 10.8

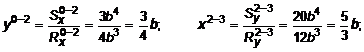
В заключении, проверим условия нахождения пластины в рав­новесном состоянии:

Уравнения равновесия удовлетворяются, следовательно, пласти­на находится в равновесном состоянии.