Вопросы к экзамену по дисциплине
“Алгоритмические основы программной инженерии”
Блок 1. Современные тенденции развития компьютерных наук и технологий.
1.Качественный переход от индустриальных технологий к потребностям новых информационных технологий. Объясните причины такого перехода. Роль квантовой теории в этом процессе.
2. Связь фундаментальных наук, включая информатику, с появлением и развитием новейших технологий.
3.Компьютерная революция. Кремниевые компьютеры и закон Мура. Границы закона Мура, принцип неопределенности Гейзенберга, квантовые ограничения.
4.Искусственный интеллект. Рациональные агенты и примеры их использования.
5. Сравнение архитектуры цифрового компьютера и архитектуры мозга человека.
6. Что будет, когда закончится кремниевая эра?
Параллельная обработка данных несколькими процессорами одновременно. Молекулярные транзисторы. Квантовые компьютеры. Открытые проблемы.
7.Чем хороши квантовые вычисления? Их связь с быстрыми алгоритмами.
8. Модели вычислений – стандартные и альтернативные. Сравнение.
9.. Перспективы развития технологий программирования в современном мире.
Блок 2. Введение в алгоритмические основы программной инженерии
1. Объекты исследования – информация и алгоритмы ее обработки.
2. Понятие алгоритма. Определение алгоритма по Колмогорову и Маркову.
3. Формализация понятия алгоритма. Какие возможности открывает перед нами формализация понятия алгоритма?
4. Общие требования к алгоритму.
5. Алгоритм Евклида. Великая теорема Ферма. Какой вопрос может быть поставлен
перед информатикой в результате анализа этих двух задач?
6. Алгоритм Евклида и примеры его использования в качестве составной части современных эффективных алгоритмов
7.. Алгоритмически разрешимые и неразрешимые задачи. Курт Гедель и его теорема о
неполноте. Ее значение для информатики.
8. Тезис Черча-Тьюринга
9 Уточнение понятия алгоритма через класс рекурсивных функций.
10.Использование рандомизированных алгоритмов для упрощения решения трудных задач. (Пример проверки того, является ли заданное число простым)
11. Примеры алгоритмически неразрешимых проблем.
12.. На какие вопросы отвечают теория вычислимости (теория алгоритмической
разрешимости), теория сложности, теория вероятности.
Блок 3 Формальные теории, формальные системы и языки.
- Дедуктивные системы. Исчисления. Формальная (аксиоматическая) теория (система).
- .Общая схема построения формальной системы. Языки – суть множества.
Свойства формальных систем. Примеры формальных систем.
- Элементы теории множеств. Теоретико -множественные операции для любых множеств А и В. Свойства теоретико – множественных операций. Биекция. Понятие континуума. Сравнение множеств натуральных, целых, рациональных и вещественных чисел. Равномощны ли они? Канторовское понятие мощности множества.
- Элементы комбинаторики в приложении к множествам. Задачи, решаемые комбинаторными методами. Три основных правила счета. Примеры.
5 Языки общения с ЭВМ и программы для обработки языков.
6. Алфавит, слово, язык в программировании. Подслово, префикс, суффикс.
7 Примеры языков над алфавитом 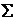 ={a,b}.
={a,b}.
Блок 4.Теория алгоритмов. Алгоритмические проблемы. Конечные автоматы. Машина Тьюринга.
1 Характерные черты алгоритма. Дискретность. Детерминированность, Пошаговость. Массовость. Результативность
2. Понятие эффективно вычислимой функции. Класс частично рекурсивных функций. Что соответствует в императивном программировании частично рекурсивным функциям?
3. Алгоритмические проблемы. Проблема принадлежности слова языку.
4. Конечные автоматы (КА)– простейшая вычислительная модель. Как происходит моделирование процесса вычислений с помощью КА?
5 Основные компоненты КА. Определение КА как формальной системы. Диаграмма состояний. Пример задачи.
6. Машина Тьюринга. Задание алгоритмов посредством Тьюринговых функциональных схем. Пример задачи.
7. Проведите сравнение введения понятия алгоритма с помощью рекурсивных функций и с использованием машины Тьюринга.
8.Базовые алгоритмы обработки данных
9. Алгоритмы поиска и выборки -пример
10. Алгоритмы сортировки –пример.
11. Сравнение алгоритмов на основе функции трудоемкости. Понятие трудоемкости алгоритма. Худший, лучший и средний случаи трудоемкости алгоритма.
12.Пример анализа трудоемкости алгоритмов. Задача суммирования элементов
квадратной матрицы –количественно-зависимый алгоритм.
13. Пример анализа трудоемкости алгоритмов. Задача поиска максимума в массиве -
количественно-параметрический алгоритм.
14. Асимптотический анализ функций. Классификация скорости роста сложности
алгоритма. Классы функций 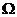 (f), O(f),
(f), O(f), 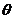 (f). Их сравнительный анализ.
(f). Их сравнительный анализ.
15.Рекурсивные функцию Понятие вычислимой функции. Простейшие эффективно
вычислимые функции.
16 Деление функций на примитивно рекурсивные, частично рекурсивные и
общерекурсивные. Их соответствие программным блокам императивного
программирования.
17 Работа с графами.
18. Как хранить графы в памяти компьютера?
Каковы структуры данных для представления графов?
19 Теория сложности. На какие вопросы отвечает теория сложности? Классификация задач по классам сложности. Класс P. Класс NP. Класс NPC. Открытые проблемы.