Трехфазный АИН с ШИМ должен формировать мгновенные значения напряжений (средние за период несущей частоты) на трех фазах. Переключение каждого вентиля изменяет напряжения на всех фазах. Это осложняет разработку алгоритма управления вентилями. Управление упрощается, если формировать не фазные напряжения (векторы фазных напряжений), а перейти к формированию пространственного (не временного вектора), введенного в теории электрических машин. Согласно этой теории три симметричных фазных напряжения при отсутствии нулевого провода могут быть представлены одним пространственным вектором (space vector), однозначно определяющим эти напряжения. В литературе этот вектор называют также обобщенным вектором, результирующим вектором, коммутирующим вектором. Пространственный вектор 
расположен в плоскости перпендикулярной оси вращения ротора.
Вектор, расположенный на плоскости, имеет две координаты. В полярной системе ― это модуль U и угол θ, отсчитываемый против часовой стрелки от полярной оси до направления вектора. В прямоугольной системе координат вектор выражается через проекции на вещественную ось α и мнимую ось β.
Вещественную ось обычно совмещают с осью фазы «A ». Тогда для фазы «A » угол θ = 0. Для произвольного угла за период несущей частоты вектор U запишется так
. (2.7)
Если известны мгновенные значения фазных напряжений UA, UB, UC, то пространственный вектор находится геометрическим суммированием
мгновенных значений, направленных по осям фазных обмоток (сдвинутых на 120 град.), с последующим умножением на 2/3.
, (2.8)
где a – оператор поворота на 120 град.
. (2.9)
Проекции вектора на фазные оси дают мгновенные значения фазных напряжений.
Это справедливо, если в трехфазной системе отсутствует нулевой провод и обеспечивается равенство нулю суммы мгновенных значений фазных напряжений
. (2.10)
Убедимся в этом на примерах.
Рис. 2.10. Транзисторный трехфазный мостовой автономный инвертор напряжения при соединении нагрузки звездой
На рис. 2.11, а приведена расчетная схема для состояния 1, когда проводят вентили V 1, V 2, V 6 (см. рис. 2.10). При этом фаза A соединена с шиной «+», а фазы B, C с шиной «–». Пусть напряжение питания Ud = 300 В. Тогда uA = 200 В, uB = -100 В, uC = -100 В (см. рис. 2.10, б). Геометрическая сумма этих напряжений с учетом множителя 2/3 (см. рис. 2.11, б–в)
.
Проекции вектора на оси обмоток дают исходные мгновенные значения напряжений:
UA = U cos θ = 200 В,
UВ = U cos(120°-- θ) = -- 100 B,
UC = U cos(240°-- θ)= -- 100 В.
На рис. 2.11, г приведена расчетная схема для состояния 2, когда проводят вентили V 1, V 2, V 3, а на рис. 2.11, д, е – построения для этого состояния.
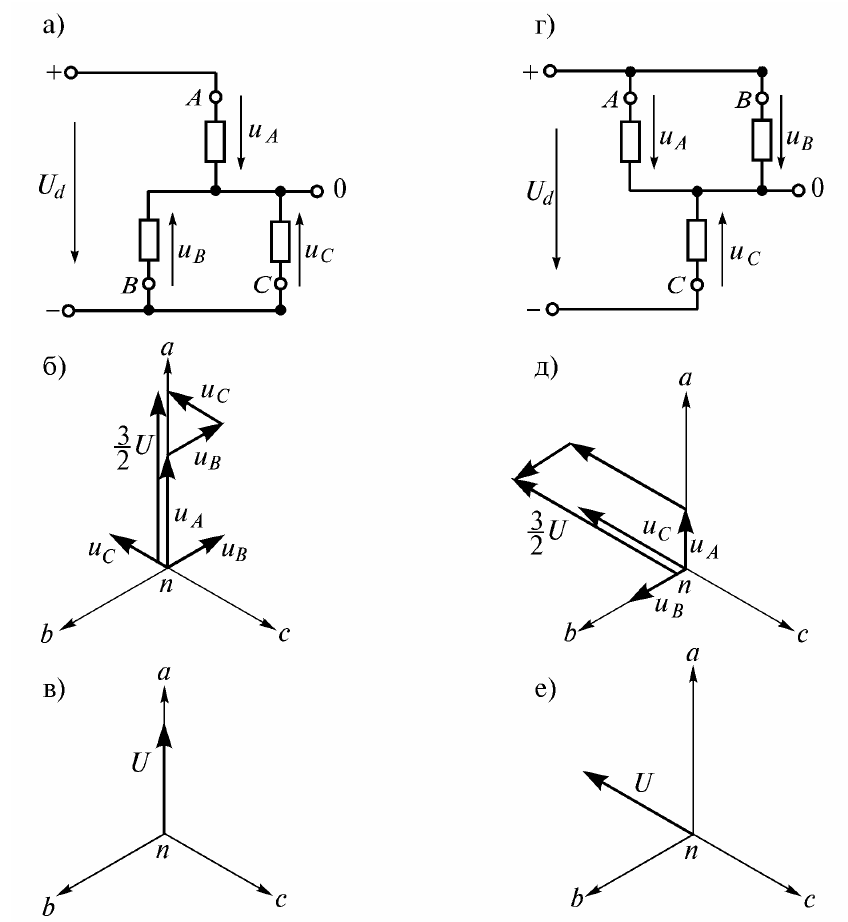
Рис. 2.11. Иллюстрация понятия обобщенный вектор: схема соединений при включении вентилей V 6, V 1, V 2 (а); построение обобщенного вектора (б); обобщенный вектор для этого случая (в); схема соединений при включении вентилей V 1, V 2, V 3 (г); построение обобщенного вектора (д) и обобщенный вектор для этого случая (е)
Таким образом, пространственный вектор находится геометрическим суммированием мгновенных значений напряжений, направленных по осям фазных обмоток (сдвинутых на 120 град.), с последующим умножением на 2/3. То есть, он однозначно определяет мгновенные значения фазных напряжений трех фаз. Заметим также, что этот вектор не требует синусоидальности напряжений.
Способ управления АИН, в основе которого лежит модуляция с помощью пространственного вектора (space vector modulation) или векторная ШИМ. Как уже говорилось, в трехфазном АИН имеется шесть возможных ненулевых комбинаций включенных состояний ключей инвертора, которые создают шесть фиксированных положений пространственного вектора выходного напряжения (табл. 2.2). Из одного положения в другое вектор перемещается скачком, поворачиваясь при каждом переключении ключей на 60° (рис. 2.12). Каждое из шести положений пространственного вектора 
рассматривается как самостоятельный вектор. При этом модуль
вектора остается неизменным и равным 2/3 Ud. Направление вектора совпадает с осью той фазы, которая одна подключена к источнику питания. Состояния схемы нумеруются i = 1, 2, 3, 4, 5, 6. Причем номер состояния определяется номером вентиля, единолично подключенным к одному из выводов источника питания. Кроме того, есть два положения, при которых включены либо все три верхних ключа инвертора (V 1, V 3, V 5), либо все нижние вентили (V 2, V 4, V 6). При этом напряжение на выходе инвертора равно нулю. Такому состоянию ключей соответствует нулевой вектор 
.
Таким образом, шесть ненулевых векторов
и два нулевых вектора называются базовыми векторами напряжения (см. табл. 2.2, рис. 2.12). Секторы между базовыми векторами обозначены цифрами 1, 2… 6. Последовательный переход от одного базового вектора к другому соответствует ступенчатой форме фазных напряжений (см. рис. 2.11). Для получения формы фазных напряжений, близкой к синусоидальной, нужно, чтобы пространственный вектор напряжения двигался, если и не абсолютно плавно, то хотя бы малыми скачками, занимая положения и между базовыми векторами. Этого можно добиться, если внутри каждого периода широтно-импульсной модуляции использовать не один исходный базовый
вектор, а линейную комбинацию исходного и следующего за ним ненулевого базового вектора, а также один из нулевых векторов. Пусть требуемый вектор 
расположен в секторе 2 (см. рис. 2.11). Тогда переключения осуществляются между векторами 
и нулевым вектором , т. е. между замкнутыми состояниями ключей инвертора 1–2–3, 2–3–4 и 2–4–6 (см. табл. 2.2).
Рис. 2.12. Базовые пространственные вектора
Задача управления инвертором формируется следующим образом: задано требуемое в данный момент времени положение пространственного вектора напряжения, т. е. его модуль Um и угол поворота θ. Требуется найти весовые коэффициенты γ 1, γ 2, γ 0, определяющие относительные продолжительности включения комбинации ключей инвертора, соответствующих используемым базовым векторам, т. е. относительные время включения ключей 1–2–3, 2–3–4 и 2–4–6, соответственно, для случая работы инвертора во втором
секторе. Для второго сектора пространственный вектор напряжения может быть описан следующими уравнениями:
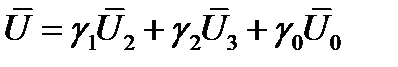; (2.11)
. (2.12)
Здесь γ1, γ2, γ0 – относительные продолжительности включения комбинации ключей 1–2–3, 2–3–4 и 2–4–6, которые соответствуют базовым векторам 
и .
Относительные продолжительности γ1, γ2, γ0 находятся следующим образом:
γ 1= t 1/ TШИМ ; γ 2= t 2/ TШИМ; γ 0= t 0/ TШИМ, (2.13)
где t 1, t 2, t 0 – промежутки времени включения этих векторов в течении времени TШИМ.
Т а б л и ц а 2.2